例谈高中解析几何常考的几种问题

◎卢桂英

一、解析几何常考的几种问题以及应对方法

1.求参数的值的问题 求参数值的问题一直是高考中最重要的考点之一，常常会以选择题的形式出现在试卷之中。求参数值问题主要考察我们对曲线的性质的认识能力，应对这种问题，我们应当从曲线的性质入手，根据他们的变量关系构造方程[1]。

【2016年2卷4题】圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1，则a=

【解析】圆x2+y2-2x-8y+13=0化为标准化方程为（x-1）2+（y-4）2=4，所以圆心为（1，4），，由此我们可解得a

2.存在性问题 存在性问题是解析几何中考察考生对曲线性质以及平面坐标系的认识深度的重要题型，学生们需要根据平时所学的知识并运用几何思想来分析问题。存在性问题多以是否存在这样的常数作为问题的核心探索思路，例如是否存在这样的常数，这样的点这样的直线或者这样的圆。我们只要根据掌握的圆锥曲线的基本性质，转化条件，优选解题方法，这类问题自然就迎刃而解了[2]。

（I）当K=0时，分别求C在点M和N处的切线方程；

（II）y轴上是否存在点P，使得当 K变动时，总有∠OPM=∠OPN？说明理由。

【解析】针对于（II）的问题，我们可以先做出简单判断，然后利用设而不求的思想将点代入曲线C的方程，将其转化成关于x的一元二次方程，化几何问题为代数问题，设出M，N的坐标和P点坐标，将直线PM，PN的斜率和用a表示出来，直线PM和PN斜率为0，即可求出a，b关系，从而找出合适条件的P点坐标。

存在符合题意的点，证明如下：

设 P（0，b）为符合题意的点，M（x1，y1），N（x2，y2），直线PM，PN的斜率分别为 k1，k2，

将y=kx+a代入C的方程整理得x2-4kx-4a=0。

x1+x2=4k，x1x2=-4a

当b=-a时，有k1+k2=0，则直线PM的倾斜角与直线PN的倾斜角互补

所以∠OPM=∠OPN，所以 P（0，-a）符合题意。

3.考察圆锥曲线的基本概念和性质 圆锥曲线的基本概念和性质是整个解析几何的基础，随着近几年高考题目的不断改革，高考中解析几何的问题也随之从探索性问题转变到考察学生的基础性问题上来，考察圆锥曲线的基本概念和性质的相关问题逐年增多。考生们常常容易将双曲线与椭圆和圆的相关公式混淆，造成失分。

【解析】这是一道标准的考察考生圆锥曲线基本概念与性质的题目。做题时我们应当根据题意，找到合适方法与公式进行运算。

根据椭圆的对称性，必过P3，P4，又因为P4横坐标为1，所以椭圆必不过P1，过P2，P3，P4三点将P2与P3的坐标代入椭圆方程可得a2=4，b2=1

4.利用向量求曲线方程和解决相关问题 这部分问题通常放在高考试卷的最后，也就是我们俗称的压轴题，它考察了学生对直线与椭圆的理解能力以及运用双曲线和平面向量等综合知识去解决实际问题的能力。想解决这部分问题，要求学生们对数形结合，方程转化有比较深入的理解，同时要具备很强的综合分析和探索能力[4]。

【2016年三卷20题】已知抛物线C：y2=2x的焦点为F，平行于x轴的两条直线l1，l2分别交C于A，B两点，交C的准线于P，Q两点。

（I）若F在线段AB上，R是PQ的中点，证明AR//FQ；

（II）若△PQF的面积是△ABF的面积的两倍，求 AB中点的轨迹方程。

记过A，B两点的直线为L，则L的方程为2x-（a+b）y+ab=0。

由于F在线段AB上，故1+ab=0.

记AR的斜率为k1，FQ的斜率为k2，则

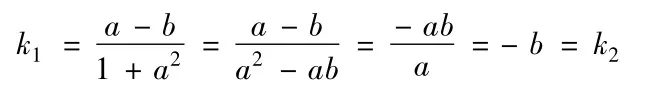
所以可证明AR//FQ.

（Ⅱ）设 l与 x轴的交点为 D（X1，0），

设满足条件的AB的中点为E（x，y）.

当AB与x轴不垂直时，由KAB=KDE可得.

当AB与x轴垂直时，E与D重合.所以，所求轨迹方程为y2=x-1

5.最大（小）值问题 最大（小）值问题也就是我们常说的最值问题，其出题形式多为求解某变量的最大值或者最小值，或者是取值范围。我们可以通过代入法来建立关于求解目标的变量函数，通过运用基本的不等式或者构造函数的方法来解函数的最值。

（I）当 t=4，AM=AN时，求△AMN的面积；

（II）当2AM=AN时，求k的取值范围。

二、结束语

随着近年来高考的不断改革，解析几何在高考数学中的难度在不断下降，然而它的分值比重仍然很大，一般会占据22分左右，所以解析几何的教学应当引起我们足够的重视。只要牢牢掌握圆锥曲线的基本概念和性质，配合相应的解题思路以及数形结合的思想，就能将参数值问题、存在性问题、最值问题以及综合应用问题完美解决，保证了学生分数的提升。