最小角回归算法(LAR)结合采样误差分布分析(SEPA)建立稳健的近红外光谱分析模型

熊 芩，张若秋，李 辉，陈万超，杜一平*

(1.华东理工大学 化学与分子工程学院 上海市功能性材料化学重点实验室，上海 200237；2.德宏师范高等专科学校 理工系，云南 德宏 678400)

近年来，近红外光谱(Near infrared spectrum，NIR)技术得到广泛应用，但由于NIR数据通常存在严重的共线性问题，对其进行降维和变量选择的研究一直是该领域的研究热点。经典的降维方法，如主成分回归(PCR)和偏最小二乘回归(PLS)，虽能实现维度的大幅度降低，但模型中仍包括所有变量(波长)的信息，模型缺乏可解释性。有效解决变量共线性的另一方式为变量选择，近年提出了很多变量选择算法，如：无信息变量消除法(UVE)、蒙特卡洛无信息变量消除法(MCUVE)[1]、移动窗口偏最小二乘法(MWPLS)、竞争自适应重加权采样法(CARS)[2]、稳定性竞争自适应重加权采样法(SCARS)[3]、遗传偏最小二乘法(GA-PLS)等，这些方法已被广泛应用于光谱变量的选择中。

最小角回归(Least angle regression，LAR)算法由Efron等[4]提出，常用于回归分析和高维数据的特征选择[5-7]，在光谱建模中应用较少。该算法在前向梯度算法的基础上，逐步前进、步长适中，无需进行大量迭代运算，大大降低了计算复杂度，提高了运行速度。Liu等[8]利用LAR对脐橙的近红外数据集进行了回归预测，相较于PLS模型具有更好的预测性能和解释性，同时运行速度快于最小二乘支持向量机(LS-SVM)。颜胜科等[9]通过LAR将系数不为0的变量作为初步筛选的变量，进一步结合GA-PLS再次筛选波长，从光谱数据中提取出信息变量，预测精度优于全光谱模型。

建立NIR模型通常需将样本集划分为校正集、交互检验集、验证集等，而不同的划分会得到完全不同的模型。针对这一问题，本课题组[10]基于模型集群分析(MPA)[11]提出采样误差分布分析(Sampling error profile analysis，SEPA)算法。SEPA通过蒙特卡洛采样(MCS)获得多个(比如800或2 000)数据划分，建立多个子模型，对子模型的误差分布进行统计分析，从而解决了单次划分导致的偶然性问题，并成功应用于PLS模型优化和评价[10]以及模型传递[12]。Zhang等[13]还将SEPA与最小绝对收缩和选择算子(LASSO)[14]相结合，提出了SEPA-LASSO的变量选择方法，相较于SCARS、MCUVE、MWPLS等方法，SEPA-LASSO选择更少的变量，获得了更优异的预测性能。本文采用SEPA的思路，基于LAR回归系数提出了一种SEPA-LAR的变量逐步筛选方法，用于建立稳健的近红外分析模型。通过3套近红外数据进行建模分析，并与PLS、MCUVE、MWPLS、CARS等方法进行了比较。

1 理论与算法

1.1 最小角回归

矩阵Xn×p表示NIR光谱矩阵，n为样本数，p为变量数，yn×1表示指标向量。

最小角回归算法与经典的前向梯度回归算法(Forward stepwise regression)类似，首先将所有变量回归系数的初值赋为0，然后找出与因变量y相关性最大的变量，假设为x1。不同于前向梯度算法，LAR将直接沿x1的方向对y逼近，直至下一个变量x2出现，使得x1、x2与当前残差具有相同的相关性，再沿x1与x2的角平分线方向找到第3个变量，以此类推。LAR算法的每一步路径均保持当前残差与所有入选变量的相关性相同。

图1 变量数为2时LAR算法路径示意图Fig.1 The path of LAR algorithm in case of 2 variables

LAR的具体运算步骤可参考文献[4]。

1.2 采样误差分布分析(SEPA)

以交互检验的计算过程为例，按3个步骤对SEPA(SEPA-CV)进行说明：设采样次数为N，首先通过MCS将样本集合划分为校正集和交互验证集，获得N个不同的样本集合划分；然后分别对各样本集合建立校正模型，并计算其交互验证预测均方根误差(RMSECV)，对所有得到的N个RMSECV误差数据进行统计分析；最终综合考虑RMSECV中位数及其标准偏差(STD)，以及误差分布轮廓(倾向于正态分布的优先选择)来选择隐变量。由于采用随机选择样本集划分，并多指标综合考虑误差分布，因此所选择的参数和建立的模型更加稳健。

1.3 最小角回归结合采样误差分布分析(SEPA-LAR)建立稳健模型

SEPA-LAR的基本思路是通过N次Monte Carlo采样得到N个划分，对每个划分进行LAR计算获得不同的变量选择集合以及各变量集合下的LAR回归系数，对同一变量数集合，N个划分将得到N个变量选择结果。对相同变量数集合下的回归系数进行统计分析，统计各变量回归系数的绝对值之和，其值越大说明该变量越重要，因此选择回归系数绝对值之和最大的若干个变量作为候选的变量选择集合。利用这些变量集合建立PLS模型进行交互检验，以确定最佳变量集合进行建模。

SEPA-LAR步骤如下：

①通过N次MCS，得到N个不同的样本子集(校正集和验证集)，其中校正集的样本数均为n。对每个子集进行LAR计算，得到n-1个变量选择集合(其变量数i为1～n-1)。N个子集的所有变量选择集合共计N×(n-1)；

②对每一变量数i的所有变量选择集合(N个)，统计每个变量的回归系数绝对值之和，将该值进行降序排列，选择前i个变量。可获得i从1到n-1的n-1个变量子集；

③采用SEPA和PLS进行交互验证，计算各变量子集下的RMSECV，以RMSECV中位数和STD为依据选择最佳变量子集；

④在最佳变量子集下，利用SEPA-PLS选择最佳隐变量数；

⑤用最终选定的最佳变量子集以及隐变量数建立PLS模型，并用独立验证集对模型进行评价。

1.4 计算方法

所有计算在MATLAB(Version 2010a，The MathWork，USA)环境中自编程序完成，所有数据均进行均值中心化处理，以消除光谱的绝对吸收值，突出样品间差异。对比方法PLS、MWPLS、MCUVE以及CARS的隐变量数目由十折交互检验确定，其中，MWPLS窗口大小设为15，MCUVE迭代次数设为100，CARS迭代次数设为100。

对整个数据用Kennard-Stone(K-S)方法[15]划分出一定数目的样本组成独立验证集，用以评价模型。其余样本进行SEPA-LAR计算和PLS建模。在SEPA-LAR算法中，MCS采样次数N均设为2 000，随机抽取的校正集和验证集比例设为60∶40应用在“1.3”模型的步骤①和③。

2 数据集

2.1 玉米数据集

数据集下载自http://www.eigenvector.com/data/Corn/index.html，包含80个玉米样本的近红外光谱数据，波长范围1 100～2 498 nm，分辨率为2 nm，共700个波长点。本文采用m5仪器测得的光谱数据和玉米样品的湿度数据，湿度在9.377%～10.993%之间，独立验证集有20个样本。

2.2 柴油数据集

数据下载自http://www.eigenvector.com/data/SWRI/index.html，为柴油样本的近红外光谱数据，波长范围750～1 550 nm，分辨率2 nm，共401个波长点。本文采用密度数据，密度为0.781 8～0.872 8 g/mL。共395个样本，独立验证集195个样本。

2.3 奶酪数据集

奶酪样本购于上海某大型连锁超市，产自8个不同品牌厂家，共107个样本。用微型近红外光谱仪(INSION近红外检测器，德国)采集光谱，波长范围909～1 860 nm，分辨率为8 nm，共116个波长点。奶酪中脂肪含量采用GB 5009.6-2016碱水解法[16]进行测定，含量范围为8.21～26.65 g/100 g，平均含量为19.51 g/100 g，独立验证集37个样本。

3 结果与讨论

3.1 玉米数据集预测

利用K-S方法选择的60个样本进行SEPA-LAR以及PLS建模，其余20个样本为独立验证集。

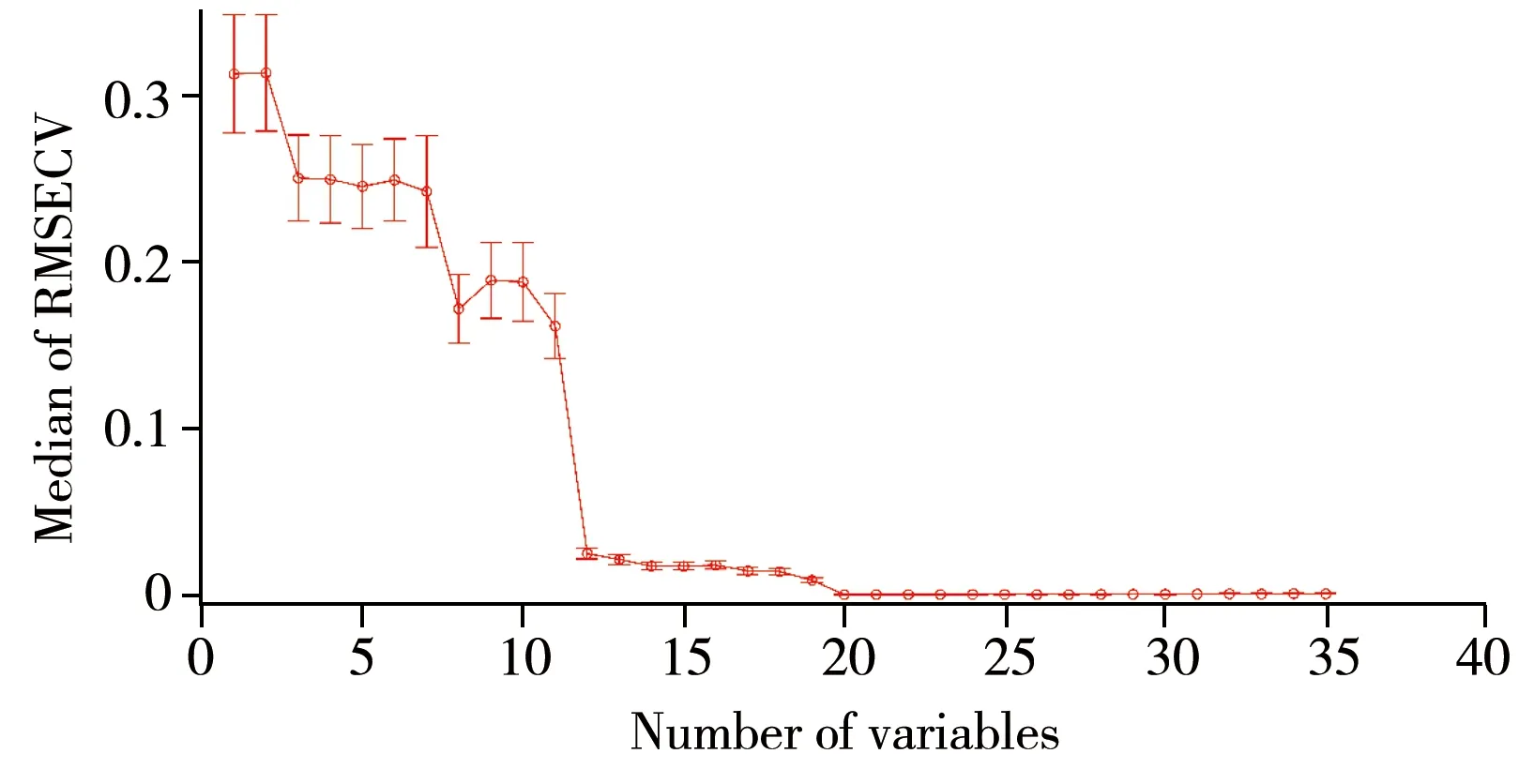
图2 基于SEPA的不同变量数的交互检验结果Fig.2 Variation of RMSECVs with the number of variables based on SEPA

图3 玉米数据中SEPA-LAR、MCUVE、MWPLS以及CARS选择的变量Fig.3 The variables selected by SEPA-LAR,MCUVE,MWPLS and CARS on corn dataset

3.1.1变量选择采用MCS方法从60个样本中随机抽取24个样本作为验证集，剩余36个样本组成校正集。经LAR计算得到35个变量子集(变量数i=1,2,…,35)。不同变量选择下的交互检验结果见图2，其中横坐标表示变量数。由图2可见，当选择的变量数低于20时，RMSECV随着变量数的增加明显减小，当变量数达到20之后，RMSECV下降趋于平缓，同时STD(图2中的误差棒)很小。由此可见，所选的20个变量对于预测玉米湿度具有重要作用，因此最终选择20个变量用于PLS建模。当变量数为20时，各变量回归系数绝对值之和的统计结果表明，大部分的波长变量未被LAR选中，而某些特征变量可被LAR选中。LAR能够筛选出相关性大的变量并赋予其回归系数，而将其余变量的回归系数直接赋值为0。由于集合划分的不同，不同样本子集下，LAR并非选中同样的波长变量，SEPA在建模中充分考虑了集合拆分的影响，最终选择的特征变量是基于大量重复采样后的统计结果，使所建模型更合理与可靠。

图3给出了SEPA-LAR、MCUVE、MWPLS以及CARS选择的波长变量。1 900 nm与2 100 nm左右属于水分子O—H的组合频吸收谱带，1 410 nm左右属于水分子O—H的一级倍频吸收谱带[2]，该波长区域对于玉米湿度的预测具有重要作用。CARS选择了1 908、2 108 nm两个特征波长，SEPA-LAR和MCUVE均选择到该重要吸收谱带内的波长，且两种方法所选波长基本一致，但SEPA-LAR选中的波长变量更少，其预测精度更高。MWPLS则选择了更多的波长变量，未选中包含2 100 nm左右的特征波长。

3.1.2模型的评价利用SEPA-LAR选择的变量以及SEPA-CV确定隐变量数，建立PLS模型，同时分别采用全谱以及MWPLS、MCUVE、CARS波长选择方法筛选出特征变量建立PLS模型，利用独立验证集评价上述模型，表1给出了SEPA-LAR及其他4种方法建模结果的比较。由表1可知，对于独立验证集，全谱PLS模型的预测均方根误差(RMSEP)为0.015 2%，MWPLS-PLS、MCUVE-PLS、CARS-PLS以及SEPA-LAR的RMSEP分别为0.029 0%、0.002 76%、0.000 314%以及0.001 44%。相较于全谱PLS建模，采用MCUVE、CARS和SEPA-LAR方法对变量进行筛选均能提高对玉米湿度的预测性能。相比MCUVE方法，SEPA-LAR通过筛选出更少的变量数，在提高建模效率的同时获得了更高的预测精度，表明SEPA-LAR对玉米湿度数据具有优异的预测性能。在玉米湿度这类变量特征性强的简单体系中，CARS方法表现优异，仅筛选出两个特征变量，预测精度优于本方法及其他对比方法。但当样品体系复杂时，CARS选择的波长子集波动较大，建模稳定性变差。而SEPA-LAR通过多指标综合考虑误差分布，模型更稳健。

表1 5种方法对玉米湿度的预测结果Table 1 Results of five methods on the corn moisture dataset

nVAR represents the number of selected variables；nLV represents the number of latent variables；RMSEC represents the root-mean-square error of calibration；RMSEP represents the root-mean-square error of prediction

3.2 柴油数据集与奶酪数据集的预测

利用SEPA-LAR对柴油数据和奶酪数据进行了变量选择和模型建立，并与全谱、MWPLS、MCUVE、CARS方法进行比较。表2为柴油密度和奶酪脂肪数据的建模结果。相较于其他4种方法，SEPA-LAR表现出更优异的建模能力，且选择的变量最少，模型的预测误差RMSEP最小。对于柴油密度数据，SEPA-LAR仅选择了28个波长，RMSEP低至0.001 58 g/mL。将SEPA-LAR应用于奶酪脂肪数据进行建模，所建模型仅含有25个波长，RMSEP为1.13 g/100 g。

表2 5种方法对柴油密度和奶酪脂肪的预测结果Table 2 Results of five methods on the diesel density dataset and cheese fat dataset

图4给出了柴油数据和奶酪数据的近红外光谱，以及4种方法所选择的波长。由图4A可见，对于柴油数据，4种方法选择的波段近似，所选波长范围集中在750～850、1 000～1 100、1 200～1 300、1 400～1 550 nm，这些区域对应柴油的近红外主要吸收峰位置。与MCUVE和CARS相比，SEPA-LAR选择的变量大都被MCUVE和CARS选中，但SEPA-LAR最终选择的变量更少，模型的预测性能更优异。

由图4B可见，4种变量选择方法选择了大体相同的波长区域，即900～1 000、1 100～1 350、1 580～1 750 nm。其中SEPA-LAR、MCUVE和CARS选择的具体波长差别较大，而SEPA-LAR的所选波长几乎均被MWPLS选中。CARS选择的波长更少，但其预测性能不如SEPA-LAR。相较于MCUVE，SEPA-LAR则选择更少的变量，模型的误差更低。研究结果表明，SEPA-LAR可在选择较少变量参与建模的同时，提高模型的预测性能。

4 结 论

本文提出了一种基于最小角回归算法和SEPA算法的变量逐步筛选方法，用于构建稳定的近红外光谱分析模型。以玉米湿度、柴油密度以及奶酪脂肪数据集为例，首先基于大量的蒙特卡洛采样计算得到的LAR回归系数统计结果得出各个变量子集，再采用SEPA框架的思路进行交互检验确定最佳变量子集，最后利用得到的最佳变量子集通过SEPA-CV确定PLS模型的隐变量数，从而建立稳健合理的近红外光谱模型。实验结果表明，相较于全谱以及MCUVE、MWPLS方法，SEPA-LAR能有效筛选出更少的特征变量，消除原始变量的共线性问题，所建模型具有优异的预测性能，稳定性优于CARS方法，相较于全谱PLS模型拥有更好的可解释性，有效提高了模型的准确性和稳定性。