周期性应变调控斯格明子在纳米条带中的运动∗
2018-08-02轩胜杰柳艳
轩胜杰 柳艳
(东北大学理学院,沈阳 110819)
斯格明子是一种拓扑稳定的手性自旋结构,凭借其在磁性赛道存储器和自旋电子器件方面的巨大应用潜力而受到研究人员的广泛关注.为了使斯格明子能够更好地应用于磁性赛道存储器,研究斯格明子在纳米条带中的运动行为就变得非常重要.本文主要研究了存在周期性应变的纳米条带中铁磁斯格明子和反铁磁斯格明子在电流驱动下的运动行为.研究结果表明:周期性应变使得驱动电流存在一个临界电流密度,只有当电流密度大于临界电流密度时斯格明子才能够在纳米条带中连续移动.临界电流密度随应变振幅的增加而增加,随应变周期的增加而减小.铁磁斯格明子在周期性应变的调制下会产生周期性运动,轨迹为波浪式,其横向速度受到边界的影响,而纵向速度则与应变梯度成正比.反铁磁斯格明子在周期性应变调控下运动方向不变,但其移动速度则剧烈变化.
1 引 言
磁斯格明子是一种拓扑稳定且表现出粒子特性的手性自旋构型,它可以在多种磁性材料中形成.科研人员首先在B20族化合物MnSi中观察到斯格明子晶体的存在[1],随后在具有体Dzyaloshinskii-Moriya(DM)相互作用的B20族的其他磁性材料[1−7]和具有界面DM相互作用的多层膜中也相继观察到斯格明子[8−10].由于斯格明子具有体积小,稳定性好,能耗低的优点,被视为下一代磁存储的信息载体.最近实验上又发现斯格明子可以在室温零场下存在,这进一步推动其走向应用[11−16].
斯格明子作为信息载体,最重要的应用在赛道存储器上.赛道存储器的信号读写通过自旋极化电流驱动斯格明子移动来实现,不像传统硬盘那样需要磁盘转动,避免了器件的损坏也提高了读写速度.因此要将基于斯格明子的赛道存储器推向应用,对斯格明子在纳米条带中的移动行为的研究就至关重要.Fert等[17]和Iwasaki等[18]首先对纳米线中极化电流驱动下斯格明子的移动行为进行了模拟,发现斯格明子沿驱动电流方向的移动速度不仅与电流密度成正比,同时与非绝热系数和阻尼系数的比值也呈正比关系.除了沿驱动电流方向的速度,斯格明子也会沿垂直电流方向移动直到马格纳斯力与边界的排斥力达到平衡为止.另外,纳米线中的缺陷也对斯格明子的移动速度有影响[18,19].斯格明子移动也非常依赖材料类型和电流的驱动方式.目前发现的斯格明子类型有“Bloch”型[2],“Neel”型[8]、反斯格明子[20,21]和反铁磁斯格明子等[22],每一种类型的斯格明子都有其独特的移动特性.电流驱动斯格明子也有两种方式,一种是电流直接通入铁磁纳米线中,利用自旋转移扭矩效应(STT)驱动斯格明子,另一种是将电流通入重金属层中,通过自旋霍尔效应(SHE)产生的自旋电流驱动斯格明子.两种不同的驱动电流作用于不同类型的斯格明子上,会有不同的移动方向和速度[23].除了通过改变材料类型、电流驱动方式来调控斯格明子的移动外,Kang等[24,25]也提出利用电压改变材料各向异性以调控斯格明子的运动.在实际材料中,材料本身内部还有可能存在应变,或者可以通过施加应力的方式也可以使材料产生应变.应变的存在会在体系内引入磁弹性能而改变体系能量,进而改变磁矩分布[26−30].利用应变调控斯格明子已经在铁磁结构中得到了证明[31−33].日本的Shibata等[31]证明了单轴拉伸应变使斯格明子变形并引起磁结构的变化,我们近期的研究也证明了单轴应变能切割条纹畴产生斯格明子[33].因此,研究应变对纳米条带中斯格明子的移动行为的影响是一个值得关注的课题,该研究既有利于解释实际材料中由于材料本身内部应变引起的斯格明子移动行为改变的现象,也可以找到利用应变操控斯格明子移动的方法.
本文通过微磁学模拟计算了存在周期性应变的纳米条带中斯格明子的运动行为,包括铁磁斯格明子和反铁磁斯格明子.研究结果表明:周期性应变使得驱动电流存在一个临界电流密度,只有当电流密度大于临界电流密度时斯格明子才能在纳米条带中连续移动.铁磁斯格明子在周期性应变的调制下会产生周期性运动,轨迹为波浪式,其横向速度受到边界的影响,而纵向速度则与应变梯度成正比.反铁磁斯格明子在周期性应变调控下运动方向不变,但其移动速度则剧烈变化.
2 模型和方法
为了充分研究周期性应变对斯格明子移动的影响,我们选取铁磁和反铁磁两种类型的材料作为研究对象.图1(a)是Co/Pt铁磁双层纳米条带示意图,Co薄膜覆盖在重金属Pt之上.在该结构中,Co与Pt的界面上存在着界面DM相互作用,因而在Co膜中可以存在Neel型斯格明子.选取的铁磁纳米条带长度为800 nm,宽度为150 nm,厚度为0.4 nm.图1(b)为KM nF3反铁磁纳米条带示意图,在该结构中存在体DM相互作用,可以存在反铁磁斯格明子.选取的KMnF3反铁磁纳米条带的长度为420 nm,宽度为42 nm,厚度为3.36 nm.两种材料的初始态都是在纳米条带左侧存在一个斯格明子,其中铁磁斯格明子是拓扑数为−1的斯格明子.两种材料中斯格明子的产生在理论上都已得到验证[34,35],本文中斯格明子是通过施加垂直极化电流产生的.为了驱动斯格明子移动,我们给纳米条带通入沿x方向的电流.
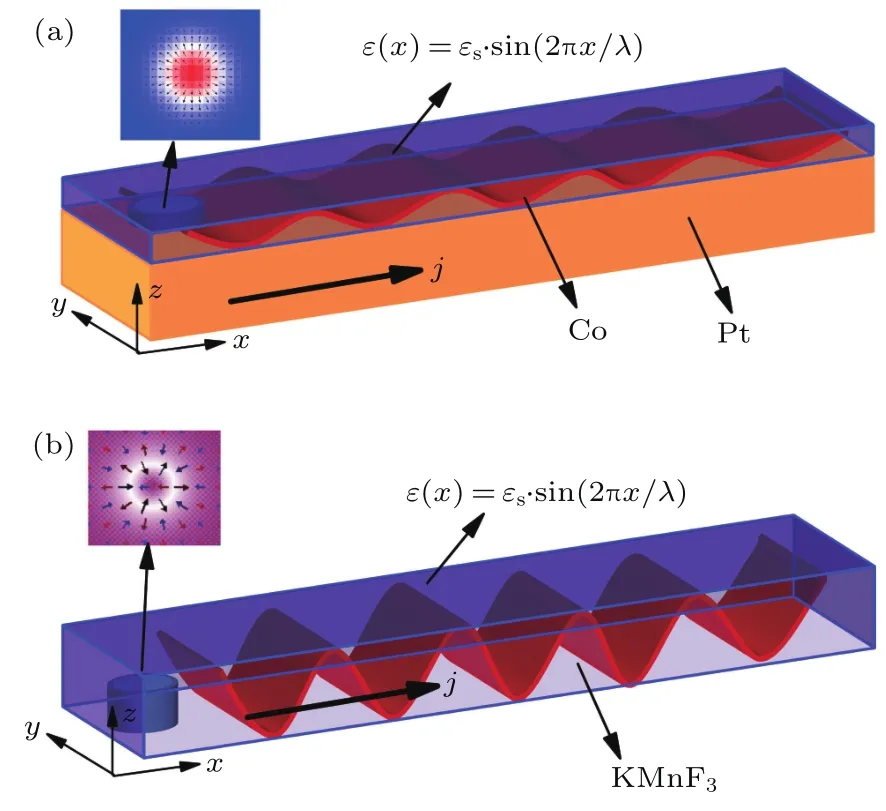
图1 存在周期性应变的纳米条带模型 (a)铁磁纳米条带模型;(b)反铁磁纳米条带模型Fig.1.The sketch of the nanotrack with sinusoidal distributed strains:(a)Ferromagnetic nanostripe;(b)antiferromagnetism nanostripe.
在该电流驱动下斯格明子的动力学行为可以用包含自旋转移扭矩的Landau-Lifshitz-Gilbert(LLG)方程来计算:
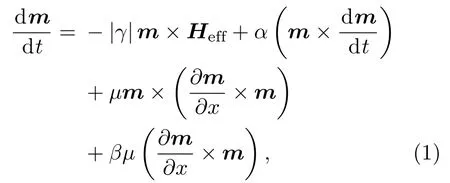
其中,m是磁矩的单位矢量,γ为旋磁比,α为LLG阻尼系数.方程后两项是自旋转移扭矩的作用项,第三项为绝热项,第四项为非绝热项,其中µ=µBjP/eMS,MS是饱和磁化强度,j是电流密度,P是自旋极化率,µB是玻尔磁子,e是电子电量,β是非绝热系数.方程(1)中的有效场可以写成Heff=−1/(µ0MS)(∂W/∂m), 其中µ0是真空磁导率,W是系统总能量.系统总能量包括DM相互作用能、交换能、退磁能、各向异性能和应变能.体DM相互作用能密度为wDM=Dm·(∇×m),而界面DM相互作用能密度为wDM=−Dm·((×∇)×m),其中D是DM相互作用常数.应变能可以写成[30]其中ε是应变,E是杨氏模量,λc是磁致伸缩系数.
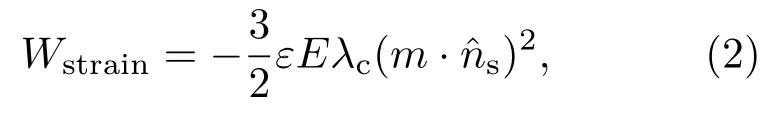
本文中我们考虑给纳米条带施加沿x方向正弦变化的周期性应变.其表达式为

其中εS是应变的振幅,λ是应变的周期.
使用包含DM相互作用和自旋转移扭矩的微磁学模拟软件(OOMMF)[36]对斯格明子的动力学行为进行模拟. 模拟中使用参数如下:Co[17]的饱和磁化强度MS=5.8×105A/m,交换常数A=15×10−12J/m,垂直磁各向异性常数K=8×105J/m3,DM相互作用常数D=3×10−3J/m2,磁致伸缩系数λc=50 ppm,杨氏模量E=2.09×1011N/m2,格子尺寸为2×2×0.4 nm3;KMnF3[37]的饱和磁化强度MS=3.76×105A/m,交换常数A=−6.59×10−12J/m,垂直磁各向异性常数K=1.16×105J/m3,DM相互作用常数D=7×10−4J/m2,磁致伸缩系数λc=50 ppm,杨氏模量E=2×1011N/m2,格子尺寸为0.42×0.42×0.42 nm3.一般情况下,阻尼系数α=0.01,非绝热系数β=0.04,自旋极化常数P=0.5.
3 结果与讨论
首先给出铁磁斯格明子的结果.图2显示了铁磁斯格明子在不同电流密度下的运动轨迹,其中λ=120 nm,εS=0.128%,图中x,y分别表示斯格明子位置矢量沿x,y方向的分量,斯格明子的位置指的是其拓扑中心的位置.我们发现电流密度较小时斯格明子不能在纳米条带中连续向前移动,其运动轨迹如图2(a)所示.斯格明子首先在电流驱动下向前移动,但在斯格明子向前运动过程中受到应变势垒的阻碍,应变势垒随着应变值的增加而逐渐增加,如果电流密度不足以克服该势垒,斯格明子就不能越过应变壁垒而折返,最终形成螺旋轨迹.当电流密度增加到至一定值时,斯格明子才可以在纳米条带中连续向前移动,但在周期性应变的调制下,其轨迹呈波浪形,如图2(b)所示.定义两种移动行为的电流密度临界值为临界电流密度jc,斯格明子在纳米条带中能形成稳定的波浪式移动的临界电流密度随应变振幅和应变周期的变化如图3所示.我们发现,临界电流密度jc随着应变振幅εS的增加而增加,随着应变周期λ的增加而减小.
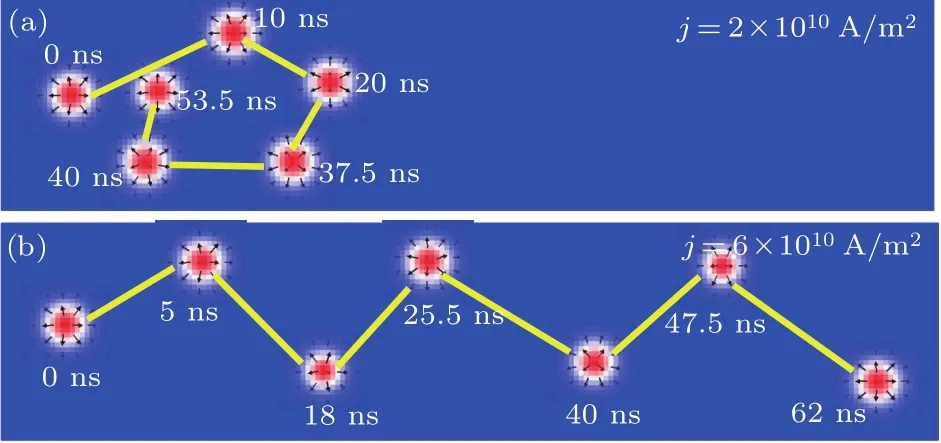
图2 不同电流密度下铁磁斯格明子的移动轨迹示意图Fig.2.The skematic trajectory of the skyrmion for different current densities.
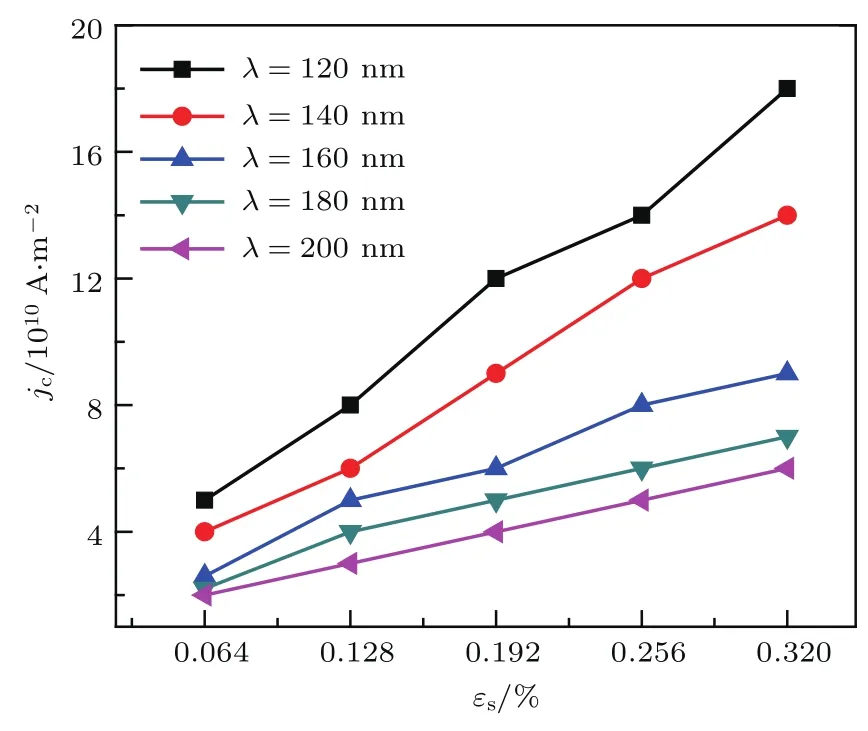
图3 不同应变周期下斯格明子能连续移动的临界电流密度随应变振幅的变化Fig.3.The threshold current density of skyrmion as a function of εS for different λ.
下面对铁磁斯格明子在纳米条带中波浪式前进的移动行为进行深入研究.图4(a)显示了电流密度j=8×109A/m2,λ=160 nm 时,不同应变振幅下斯格明子的移动轨迹.当εS=0时,斯格明子的运动轨迹是稍有倾斜的直线,这是因为在模拟过程中我们采用的参数是α=0.01,β=0.04,非绝热参数与阻尼系数之比大于1,会引起斯格明子沿+y方向移动.当施加周期性应变时,斯格明子的运动轨迹呈现波浪式,并且斯格明子在y方向上的位移随着εS增大而增大.我们进一步计算了斯格明子移动时x方向的速度vx和y方向的速度vy.图4(b)显示的是vx在不同应变振幅εS下随x的变化曲线.从图中可以看出,当εS=0时,斯格明子以恒定的速度vx运动.施加周期性应变后,vx的值出现峰值,而当仔细观察时,还可以看到谷值的存在.该峰值和谷值随着应变振幅的增加而增加,且该峰值和谷值都是周期性出现.图4(c)显示了vy随x的变化曲线,从图中可以看出,当εS=0时,斯格明子的y方向的速度vy基本为常数,而当εS=0.128%和εS=0.256% 时,vy呈现周期性变化,并且随着应变振幅的增大,vy变化的幅度也增大.

图4 (a)不同应变振幅时斯格明子的轨迹图;(b)不同应变振幅时斯格明子的v x随x的变化;(c)不同应变振幅时斯格明子的v y随x的变化Fig.4.(a)The trajectory of skyrmion for different strain amplitudes;(b)v x as a function of x for different strain amplitudes;(c)v y as a function of x for different strain amplitudes.
为了进一步分析铁磁斯格明子移动过程中速度的变化规律,图5(a)中总结了当电流密度j=8×1010A/m2,εS=0.192%,λ=160 nm时应变、斯格明子的运动轨迹、直径DS,vx和vy随x的变化曲线.从图中可以看出以下几点:1)斯格明子的轨迹、速度以及直径DS的变化周期与应变的周期完全一致,其中DS与εS变化趋势相反,本文中斯格明子的直径指的是斯格明子构型中z方向的磁矩分量mz=0所对应的圆的直径;2)vx的峰值出现在y值达到峰值时,而vx的谷值出现在y值达到谷值时,这表明当斯格明子接近纳米条带的上边界时,vx变大,形成峰值,但当斯格明子接近纳米条带的下边界时,vx变小,形成谷值;这一现象表明本文所研究的拓扑数为−1的铁磁斯格明子接近纳米条带的上边界时沿x方向的移动速度增加,而接近下边界时沿x方向的移动速度减小;图5(b)给出了vx随斯格明子纵向位置y的变化曲线,可以看出,当45 nm

图5 (a)斯格明子的运动特征参数ε,y,D S,v x和v y随x的变化;(b)v x随y的变化;(c)v y随ε/d x的变化Fig.5.(a)The movement parameters ε,y,D S,v x,and v y of the skyrmion as a functinon of x;(b)v x as a function of y;(c)v y as a function of the strain gradient dε/d x.
为了进一步验证上述结论,我们对比了电流密度j=8×1010A/m2,εS=0.064%,λ=160 nm时,斯格明子在α=β,α>β和α<β三种情况下的运动情况.图6(a)显示了α=β=0.01时斯格明子在纳米条带的移动情况.斯格明子在纳米条带中心线上下波动,vx的变化幅度很小,在7.62—7.86 m/s之间变化,并且vx的变化趋势基本是正弦曲线.当α=0.01,β=0.04时,斯格明子的整体运动趋势是向纳米条带的上边界方向移动,vx的峰值是逐渐增大的,如图6(b)所示.当α=0.04,β=0.01时,斯格明子的整体运动趋势是朝向纳米条带的下边界方向,此时vx的峰值很小,但谷值却很明显,且谷值越来越小,如图6(c)所示.以上结果进一步验证了拓扑数为−1的铁磁斯格明子的vx受到上下边界的影响是不同的,即上边界使得vx逐渐增大,而下边界使得vx减小.另外,从图中可以看出三种情形中vy的周期性变化完全相同,表明vy与上下边界没有关系,它主要是与纳米条带中应变沿x方向的变化梯度有关.
下面给出周期性应变调控反铁磁斯格明子的结果.在反铁磁纳米条带中也存在着临界电流密度值.图7(a)表示在不同应变周期下,平面电流驱动反铁磁斯格明子的临界电流密度jc随应变振幅εS的变化情况.可以看到jc随εS的增加而增加,随λ的增大而减小.与铁磁斯格明子相比,反铁磁斯格明子所需的临界电流密度更大,说明反铁磁斯格明子对应变的响应更明显.

图6 不同α和β情况下斯格明子速度随x的变化 (a)α=0.01,β=0.01;(b)α=0.01,β=0.04;(c)α=0.04,β=0.01Fig.6.The velocity of skyrmion as a function of x for different α and β:(a) α =0.01,β =0.01;(b) α =0.01,β=0.04;(c)α=0.04,β=0.01.
图7 (b)显示了应变、反铁磁斯格明子的运动轨迹、直径DS、速度v随x的变化曲线,其中λ=120 nm,εS=0.128%,j=2×1010A/m2.在电流的驱动下,反铁磁斯格明子始终沿着纳米条带的中心线运动,其轨迹是一条水平直线,并没有出现铁磁斯格明子的波浪形轨迹.虽然轨迹并没有呈现出波浪形,但是施加应变后反铁磁斯格明子的直径发生了剧烈变化,其直径DS与应变εS成反比.其次,反铁磁斯格明子的移动速度受到周期性应变的调制,也成周期性变化.其速度主要是与应变梯度有关:当应变的斜率最大时,速度v的值最小;当应变的斜率最小时,速度v的值最大.

图7 (a)不同应变周期下平面电流驱动反铁磁斯格明子运动的临界电流密度随应变振幅的变化;(b)反铁磁斯格明子的运动特征参数ε,y,D S以及v随x的变化.Fig.7.(a)The threshold current density of antiferromagnetic skyrmion driven by the in-plane current as function of εS for different λ;(b)the movement param eters ε,y,D S,and v of the antiferromagnetic skyrmion as a function of x.
从图7(b)还可以发现反铁磁斯格明子的速度变化幅度很大,最大速度vmax可以达到大约3000 m/s,最小速度vmin几乎为零,说明反铁磁斯格明子速度对应变的响应比铁磁斯格明子更加明显.综上,我们发现周期性变化的应变不改变反铁磁斯格明子的运动方向,但是可以调控其尺寸的大小以及速度的大小.
最后需要说明的是,本文中考虑的应变能采用了Kittle磁弹相互作用理论[38].而近期Hu和Wang等[39]得出了针对B20族手性磁体的普适性磁弹理论.本文所采用的应变能公式((2)式)相当于其中只考虑了z方向的应变ε33,并假设磁弹耦合系数L2=K=0所对应的情况.做如此假设是基于两点考虑:1)本文模拟的铁磁对象是Co,该材料中的DMI的来源界面交换作用,与B20磁体并不相同;2)Co是垂直各向异性很强的材料,因此垂直方向的应变对于改变斯格明子的大小有比较明显的影响.然而对于一般的立方晶系手征磁体,L2一般不为0,因此L2项对于斯格明子在周期应变场作用下的动力学行为的影响仍是个值得探讨的问题.
4 总 结
本文主要研究了周期性应变对铁磁斯格明子和反铁磁斯格明子在纳米条带中运动行为的影响.计算表明只有当电流密度大于临界电流密度时,斯格明子才能在纳米条带中连续移动.在周期性应变的调控下,铁磁斯格明子在纳米条带中波浪式前行,其运动轨迹、直径及其速度都是成周期性变化,其横向速度受到边界的影响,而纵向速度则与应变梯度成反比.周期性应变不改变反铁磁斯格明子的运动方向,但是可以调控其直径和速度,其移动速度在周期性应变的作用下剧烈变化.
