贝塞尔-高斯涡旋光束相干合成研究∗

于涛 夏辉 樊志华 谢文科 张盼 刘俊圣 陈欣

1)(中南大学物理与电子学院,长沙 410083)

2)(上海航天控制技术研究所,上海 201109)

3)(中国航天科技集团公司红外探测技术研发中心,上海 201109)

基于相干合成技术,提出了对特定离散空间分布的高斯光束阵列加载离散涡旋相位生成二阶贝塞尔-高斯(Bessel-Gaussian,BG)涡旋光束的方案.利用干涉法、桶中功率和相关系数对合成BG涡旋光束的拓扑荷、光束质量进行了定量评价及参数优化.结果表明:基于相干合成技术能够产生特定的目标BG涡旋光束,阵列子光束紧密排布时合成BG光束的光束质量更高.该方法的提出对于其他涡旋光束的产生或者涡旋光束功率的提高具有一定的参考意义.

1 引 言

涡旋光束是在传播方向上中心强度或轴向强度为零、位相具有螺旋上升或下降的梯度分布的环形光束,又称暗中空光束[1].涡旋光束凭借其独特的螺旋相位分布和携带轨道角动量的特性已成为近年来特殊光束研究中的热点[2−4].光与物质的相互作用是人类探索微观物质结构及运动规律的重要手段,而涡旋光束携带的轨道角动量能够为光与物质相互作用带来新的自由度,其携带的轨道角动量所产生的力矩可用于揭示极端强场条件下的原子物理新现象、新效应[5]等.涡旋光束不仅对大气湍流有很强的抗干扰能力,而且由于其涡旋光束轨道角动量本征态可以构建高维Hilbert空间,进而可实现高密度数据存储以及通信容量和速度的提高[6,7],并具有较强的防窃听抗干扰能力.涡旋光束与粒子之间的相互作用研究表明:涡旋光束的轨道角动量特性可实现对微观粒子的旋转[8]等.所以,涡旋光束在光束与物质相互作用新机理研究、光通信、粒子操控等方面均有着重要的应用.但目前方法获得的涡旋光束能量普遍不高,导致其应用研究的发展受到一定的制约,如光与物质相互作用新现象的出现、更长距离的光通信、粒子操控中光束与粒子的相互作用难以加强等.因此,如何获得更高功率兼具高光束质量的涡旋光束成为涡旋光束工程应用中必须要解决的问题之一[9−11].

目前,对高功率涡旋光源的研究大多着眼于单个激光器.例如,Kim等[12]利用主振荡光功率放大(master oscillator power-amplifier,MOPA)技术在谐振腔产生高光束质量的拉盖尔-高斯(Laguerre-Gaussian,LG)光束,并将LG光束耦合进多模掺镱光纤进行传输放大,实现了连续涡旋光束输出.但该方法存在信号光与模场区域失配、斜率效率较低等问题.Li等[13]采用涡旋信号光通过端面抽运Ho:YAG棒放大的高功率涡旋光束产生方法.该技术具有光路简单、空间模场面积较大,但是放大效率低、热透镜效应严重、光束质量较差等问题.事实上,由于热损伤、非线性效应等物理因素,单个激光器的输出功率不可能无限提升.相干合成技术可以通过增加光束数量来增加输出功率,通过锁定相位来保持光束质量,最终实现输出光功率的提高.与单台高功率激光器相比,相干合成方法实现的阵列式光源还在系统成本、热管理和光束控制等方面有明显的优势[14].

本文以2阶贝塞尔-高斯(Bessel-Gaussian,BG)光束为目标涡旋光束,基于相干合成技术,对相位同步的阵列高斯光束加载离散涡旋相位来获得涡旋光束的方法进行了实验研究.利用干涉法实验以及桶中功率评价函数等验证了合成涡旋光束与目标光束的相位分布和光强分布的一致性,进而验证了基于相干合成技术获得涡旋光束方法的有效性.本文详细分析了高斯光束阵列空间布局、子光束数量等参数对合成涡旋光束质量的影响,通过参数优化以获得不同拓扑荷数时的高光束质量涡旋光束.

2 理论基础

2.1 Gauss光束阵列模型

贝塞尔光束是中空的环形光束,具有螺旋相位结构.本文以此为基础将高斯光束阵列进行圆形排布用于模拟贝塞尔光束[15−17].如图1所示,圆形排布的高斯光束阵列在z轴传播的光振幅表达式[18,19]为

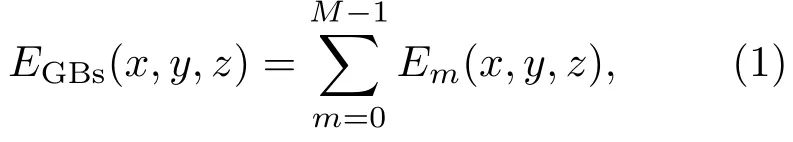
其中,

相关系数用于表征两个物理量间的相似程度.相关系数越接近于1,两个物理量的近似度越高;相关系数为0,则说明两个物理量不存在相似性.设仿真BG光束的光场分布为I1,标准BG光束的光场分布为I2,则有

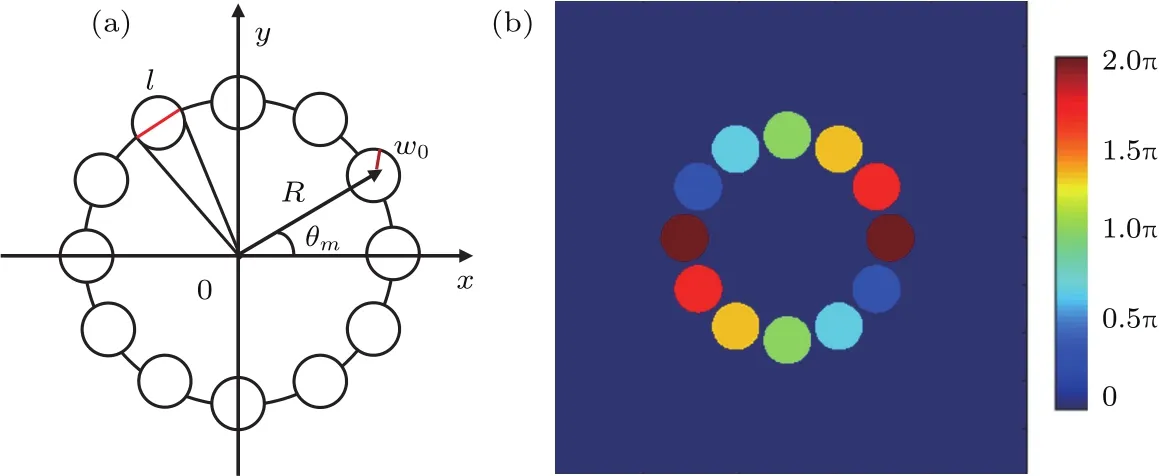
图1 高斯光束阵列的(a)空间振幅分布和(b)相位分布,其中M=12,n=2,R=0.8 cm,w 0=0.2 cmFig.1.(a)Intensity distribu tions and(b)phase distributions of Gaussian beam array for M=12,n=2,R=0.8 cm,w 0=0.2 cm.

由于BG光束的中空环形光强分布,斯特列尔比等参数不适合用于描述BG光束的远场光强分布的能量集中度.本文以目标处的桶中功率(powerin-the-bucket,PIB)作为评价合成BG光束质量的性能指标,其定义为在远场给定尺寸的“桶”中包围的激光功率占总功率的百分比,它表征光束的能量集中状态,反映了实际激光在远场的可聚焦能力[20].设桶的半宽度为b,整个光斑的半宽度为a,则有

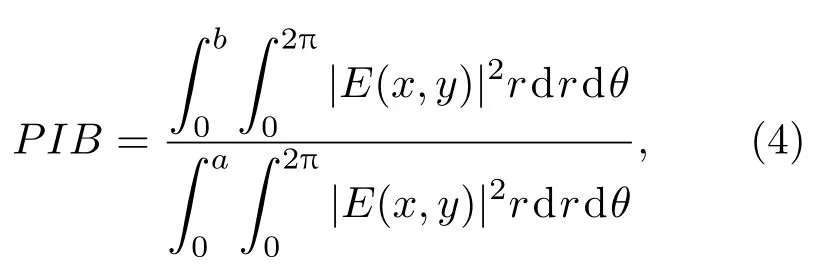
其中E(x,y)为远场振幅分布.本文利用目标处PIB作为评价合成BG光束质量的性能指标,PIB介于0和1之间,越大说明合成导致的旁瓣越少,能量更集中.

2.2 实验原理图

实验装置图如图2所示,He-Ne激光器发出的光经过扩束镜扩束5倍后,经过分束镜分束,其中一束入射到振幅型空间光调制器(SLM),将扩束后的光分成M束相同的高斯光束,此时振幅SLM所加载的灰度图如图3中所示,阵列光束经过纯相位型SLM加载拓扑荷为n的涡旋相位,最后经过合束镜、透镜后入射到电荷耦合元件(charge-coupled device,CCD)上;经分束镜分束后的参考光束被反射镜反射后入射到合束器与合成涡旋光束合束,在CCD上观察到干涉条纹.图3中的偏振片1和偏振片2的角度互相垂直,且偏振片2的角度满足纯相位型SLM的纯相位调制状态.

图2 实验光路图Fig.2.Experimental setup for the generation of a BG beam by the coherent combining technology.

相干合成的技术难点之一在于对参与合成的各子光束的精细相位控制,本实验通过振幅型SLM分束简化了相干合成中子光束初相位同步的问题.这是因为振幅型SLM[21]加载的灰度图中子光束的灰度一致,能够保证分束之后子光束的相位同步性,实现了锁相输出.

本文利用图3所示的实验装置验证了高斯光束阵列加载离散涡旋相位合成产生BG光束方法的有效性.

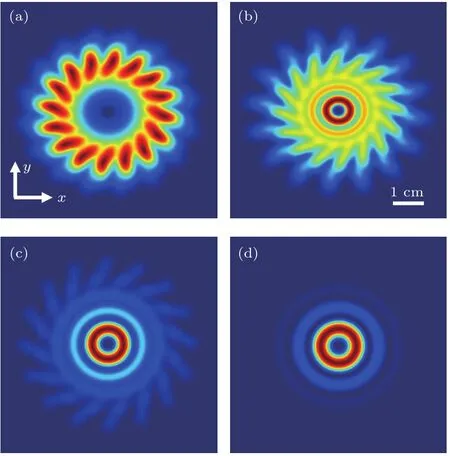
图3 合成BG光和标准二阶BG光的光强截面图 (a)z=0.6 m;(b)z=1 m;(c)z=2 m;(d)标准二阶BG光Fig.3. Comparison of the intensity distributions between coherently combined BG beam with different z and second-order BG beam:(a)z=0.6 m;(b)z=1 m;(c)z=2 m;(d)second-order BG beam.

3 结果与讨论

3.1 合成BG光束强度分布验证

根据(1)式,数值计算了M=16,n=2,R=1.1 cm,w0=0.2 cm时合成的BG光在z=0.6,1,2 m的光强分布分别如图3(a)—(c)所示,图3(d)为标准二阶BG光束的光强分布.由图3可知,在z=0.6 m时,高斯光束阵列尚没有合束形成类似BG光束的中央亮环结构;在z=1 m处,光场分布已经具有标准二阶BG光的中央亮环结构,但环外旁瓣明显.取图3(b)坐标原点为圆心到第三亮环的外环为半径,即包含了所有亮环的b=1.3 mm、包含旁瓣在内的半径a=4 mm的圆,计算了此时合成BG光的PIB=39.2%,相关系数r=0.77;z=2 m处,取b=2 mm,a=4 mm时的PIB=77.45%,r=0.901.由此可见,z=1 m时,合成BG光与标准二阶BG光的中央亮环结构相似但光束质量较差;z=2 m时,合成BG光束不仅具有与标准二阶BG光束相同的中央亮环结构,同时具有更好的能量集中度.结果验证了加载涡旋相位的高斯光束阵列能够合成BG光束.

在相同参数下计算了传播距离z=10 m的结果如图4(a)所示,图4(b)为相同参数时,用2.2节所述实验装置观察到的光强分布图.对比图4(a)和图4(b)发现,仿真和实验具有相同的中空环形光强分布,且具有相同的亮环数目.取a=2 cm以及图4(a)坐标原点为圆心到第三亮环的外环为半径即b=0.95 cm的圆为PIB的“桶”,计算了仿真获得的2阶合成BG光的PIB为91.8%,实验获得的2阶合成BG光的PIB为86.2%,即实验合成二阶BG光束的能量集中度不及仿真结果.其原因是由于实验中子光束角度、相位等参数一致性误差导致更多的环外旁瓣所致.

图4 M=16,n=2,R=1.1 cm,w 0=0.2 cm时(a)仿真光强分布;(b)实验光强分布Fig.4.Intensity distributions of coherently combined BG beam by simulation and experiment for M=16,n=2,R=1.1 cm,w0=0.2 cm:(a)Simu lation intensity distribution;(b)experimental intensity distribution.

3.2 合成BG光束拓扑荷验证

对于拓扑荷为n的涡旋光束,方位角每旋转一周波前相位会有n2π变化,根据干涉理论两束光相位相差一个2π周期干涉时会出现一个明暗条纹,相应地拓扑荷为n的涡旋光束与参考光干涉,其干涉条纹中会增加n个明暗条纹[22].实验拍摄的M=20,n=2的合成BG光与平面波的近场干涉条纹图如图5所示.由图5可知,涡旋光束与平面波干涉条纹不再是亮暗相间的竖直条纹,而是出现一个条纹分裂为3个,所以干涉图5显示的涡旋光束的拓扑荷n为2,与目标光束的拓扑荷数完全一致.

图5 M=20,n=2的近场干涉Fig.5.The near field interference fringes for M=20,n=2.

利用PIB和r参数对仿真获得的合成BG光束和标准二阶BG光束进行了定量分析,验证了合成BG光束和标准二阶BG光束的光强分布一致性.然后通过对实验获得的合成BG光束的光强图与仿真获得的BG光的光强图的定性对比以及利用PIB参数进行定量的光束质量分析,验证了合成BG光束与目标光束的光强分布一致性;最后通过干涉实验验证了合成BG光束与目标BG光束相位结构的一致性.最终验证了图3所示实验理论和装置合成BG光束的有效性.

4 涡旋光束相干合成参数优化研究

4.1 R的大小对合成的影响

M=20,n=1,w0=0.2 cm,z=10 m的不同R参数的合成BG光束光强分布图如图6所示.取a=1.5 cm,图6(c)中坐标原点到第四亮环的外环为半径即b=1.1 cm的圆为PIB的“桶”,计算了R=1.7 cm,R=1.5 cm,R=1.3 cm的PIB分别为61.7%,77.5%,81.2%.可见,保持M和w0不变,随着R逐渐减小高斯子光束阵列排布更加紧密,子光束之间的叠加程度逐渐提高,合成BG光束的环外旁瓣明显减少,因此能量集中度更高.

图6 涡旋光束光强截面图(M=20,n=1,w 0=0.2 cm) (a)R=1.7 cm;(b)R=1.5 cm;(c)R=1.3 cmFig.6.Intensity distributions of coherently combined BG beam with different R for M=20,n=1,w 0=0.2 cm:(a)R=1.7 cm;(b)R=1.5 cm;(c)R=1.3 cm.

4.2 M的大小对合成的影响

在其他参数保持不变的情况下,M=6,8,12时合成光束的光强分布如图7(a)—(c)所示,取a=1.5 cm和图7(c)中坐标原点到第三亮环的外环为半径即b=0.74 cm的圆为P IB的“桶”.M=6时合成的涡旋光斑呈空心分布,但只有一个连续的亮环,且表现出较为明显的六边形特征,桶中功率为80.2%;M=8时合成空心涡旋光斑更接近于目标光束的环形光强分布,但旁瓣明显增加,桶中功率仅为64.5%,即当M=8时可以形成n=1的合成BG光,但光束质量很差.如图7(c)所示,增加光束数量至M=12时,形成的n=1的合成BG光的PIB达到80.4%,光束质量明显提升.对M参数的分析可知,子光束之间的相位差为2πn/M,其中拓扑荷数不变时增加光束数量会缩小子光束之间的相位差,故离散的涡旋相位能更好地逼近连续涡旋相位形成质量更好的BG光.

在上述基础上,分析了M对生成n阶涡旋光束的影响.如图8所示,M=8时仅能生成n=1,2的合成涡旋光,当拓扑荷数n=3时高斯阵列没有合束形成BG光,主要是由于拓扑荷数太大而光束数量少,导致相邻子光束间附加的相位差太大而不能合成BG光束.

图7 光强分布图(n=1)(a)M=6;(b)M=8;(c)M=12Fig.7.Intensity distributions of coherently combined BG beam with different M for n=1:(a)M=6;(b)M=8;(c)M=12.

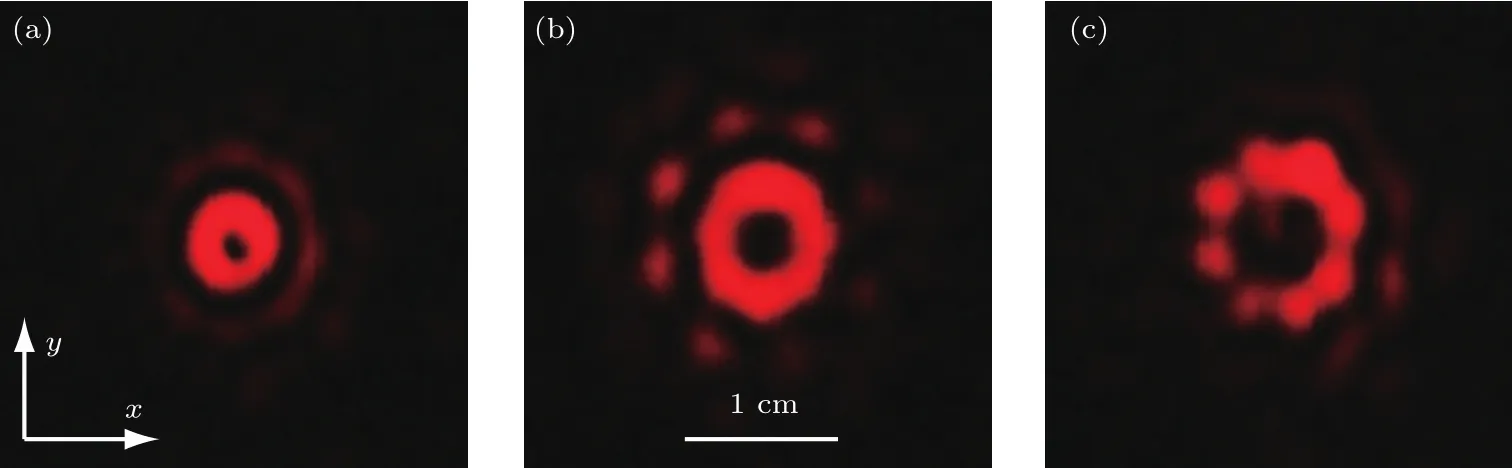
图8 光强分布图 M=8时,(a)n=1,(b)n=2,(c)n=3Fig.8.Intensity distributions of coherently combined BG beam with different topological charges for M=8:(a)n=1;(b)n=2;(c)n=3.

对比图9(b)和图10(b)可知,取a=1.5 cm和图10(a)中坐标原点到第四亮环的外环为半径即b=0.85 cm的圆为PIB的“桶”.同样n=3的合成BG光,M=20的光斑的旁瓣明显比M=12时的少且光斑均匀,光束质量更好,桶中功率由M=12时的76.6%提升至M=20时的91.8%;对比图9(c)和图10(c)可知,光束数量从12增加至20时,M=20生成了n=5的合成BG光.对M参数的分析可知,子光束之间的相位差为2πn/M,其中拓扑荷数不变时增加光束数量会缩小子光束之间的相位差,故离散的涡旋相位能更好地逼近连续涡旋相位形成质量更好的BG光.

图9 光强分布图 M=12时,(a)n=1,(b)n=3,(c)n=5Fig.9.Intensity distributions of coherently combined BG beam with different topological charges for M=12:(a)n=1;(b)n=3;(c)n=5.

图10 光强分布图 M=20时,(a)n=2,(b)n=3,(c)n=5Fig.10.Intensity distributions of coherently combined BG beam with different topological charges for M=20:(a)n=2;(b)n=3;(c)n=5.

4.3 w0的大小对合成的影响

M=16,n=2,R=1.1 cm,z=10 m,不同w0的合成BG光束光强分布如图11所示.取a=2.5 cm和图11(c)中坐标原点到第三亮环的外环为半径即b=0.95 cm的圆为PIB的“桶”,分别计算了w0=0.1 cm,w0=0.15 cm,w0=0.2 cm的P IB分别38%,67%,86.2%.说明保持其他参数不变,随着w0逐渐增大,子光束之间的间距逐渐缩小,子光束之间的叠加程度得到提高,合成BG光束的环外旁瓣明显减少,因此能量集中度更高.

图11 涡旋光束光强截面图 M=16,n=2,R=1.1 cm,z=10 m时,(a)w0=0.1 cm,(b)w0=0.15 cm,(c)w0=0.2 cmFig.11.Intensity distribu tions of coherently combined BG beam with different w0 for M=16,n=2,R=1.1 cm,z=10 m:(a)w0=0.1 cm;(b)w0=0.15 cm;(c)w0=0.2 cm.

通过对M,w0和R的分析,定义了光束阵列排布的占空比(光束阵列圆形排布的紧密程度)k=lM/2πR,设l≈2w0,可得到k=w0M/πR.通过改变束腰半径w0、组束环半径R和光束数量M来控制k的大小.通过对k中各个参数的研究发现,高斯光束阵列圆形排布的紧密程度对合成的涡旋光斑质量有显著的影响,改变参数使占空比k≈1时可获得最佳的合成效果.

5 结 论

本文基于相干合成技术提出了利用高斯光束阵列加载离散涡旋相位获得2阶合成BG的方法,通过实验与理论的光强分布对比、干涉实验、PIB和相关系数等参数,从实验上论证了这种方法的有效性.通过对高斯光束阵列的空间排布和子光束数量的研究,得到了占空比接近1时可以获得最佳光束质量的合成BG光.但本文没有考虑相干合成过程中的相位控制和环境噪声,只是从高斯光束阵列加载离散涡旋相位的角度验证了相干合成技术用于生成高功率涡旋光束方法的有效性,对用相干合成技术产生高功率涡旋光束和合成其他类型的涡旋光束有一定的指导意义.