基于Voronoi节理模型的碎裂岩边坡稳定性分析

严 豪，宋彦辉，2，陈子玉

(1.长安大学地质工程与测绘学院，陕西 西安 710054；2.西部矿产资源与地质工程教育部重点实验室，陕西 西安 710054)

0 引言

岩质边坡的稳定性不仅与组成斜坡的岩性、坡高、坡度、坡型等有关，更主要受控于斜坡中岩体结构面的分布和组合关系，对于硬质岩来说更是如此。因此，无论采用解析方法还是数值模拟方法研究边坡的稳定性，都不能忽略岩体结构面的存在。前人在这方面进行了大量的研究工作，并发展了诸多针对斜坡块体的稳定计算方法及考虑结构面的数值模拟方法如离散单元法、拉格朗日分析法及有限元法等，使得斜坡稳定分析结果的可靠性越来越高。尤其是数值模拟方法的不断发展，突破了原来极限平衡法计算边坡稳定性的限制，从而能够获得更多关于边坡应力-应变场、发展演化及破坏机制等众多信息，为更全面评价斜坡稳定性提供了强有力的支持。然而，由于斜坡岩体结构的复杂性以及结构面力学参数取值等问题，使得目前对这一问题仍未获得令人十分满意的结果。

从成因上，结构面分为原生结构面、次生结构面和表生结构面。其中原生结构面是伴随岩石形成过程产生的，包括沉积岩的层面、岩浆岩的流面及变质岩中各类变质结构面等。这类结构面从宏观上控制着斜坡的结构类型；次生结构面指岩石形成后在构造作用下产生的各种破裂形迹，广泛发育在各类岩石斜坡中，如断层、节理等。由于构造活动的多期性，岩体中往往发育多组结构面，这些次生结构面叠加在原生结构面之上，使得岩体斜坡结构更加复杂；表生结构面则是指风化、卸荷作用条件下近地表岩石产生的以张性破裂为主的节理裂隙，往往影响斜坡浅部数米到数十米的范围。

不少研究者根据斜坡的结构类型研究了它们的破坏机理和过程，并对某些边坡提出了相应的稳定分析方法[1-2]，然而对大多数边坡来说，上述研究仍仅限于定性分析和传统的极限平衡分析方法，没有针对不同结构边坡类型发展相应的稳定性评价方法。

本文主要针对一类碎裂岩边坡进行有限元分析，碎裂岩中的节理裂隙采用Voronoi图的节理网络进行模拟，并对比了该模型与碎裂岩边坡等参数、均值假设、不考虑节理条件下的计算结果。

1 Voronoi节理模型

1.1 Voronoi图的基本特征

Voronoi 图的概念最早是由俄国数学家M.G. Voronoi 在1908年提出的，并将其扩展至高维空间。1934 年，B.Delaunay从Voronoi 图中演化出分析应用的三角形网(Delaunay 三角化或Dirichlet 棋盘 )。随着计算机技术的发展， Voronoi 图的研究与应用越来越多，它们在几何形体重构、计算机图形学、图形处理与模式识别、城市规划及地理学系统等得到了广泛应用[3]。

Voronoi 图又可称为镶嵌棋盘图，它是将某一空间划分成一系列Voronoi凸多面体的理论。对于空间内任意给定点集{Pi}，i=l，2，…，n，可将空间分解为一组凸多边形几何体Vi，i=1，2，…，n，Vi包含Pi，称之为Pi的领域，Pi称为领域Vi的特征点。这样的凸多边形几何体结构称为Voronoi图。对于二维空间，Voronoi图将平面分解为一系列凸多边形，连接所有的具有共同Voronoi边界的特征点而形成的几何结构，称为Delaunay三角形[4](图1)。

图1 Voronoi图的构成Fig.1 Constitution of Voronoi convex polygon

Voronoi图的特点是任意一个凸多边形的边都垂直平分特征点(Pi)与该边另一侧的相邻特征点的连线。

根据上述Voronoi图的定义和特征，可用之模拟岩体结构，其中Voronoi多边形可看做岩石块体，而构成多边形的边可用来模拟岩体中的节理，这种岩体结构类型可代表碎裂结构或镶嵌碎裂结构岩体。

1.2 Voronoi节理模型的生成

经典的Voronoi图是通过随机过程生成的互不重叠的凸多边形。在岩体结构研究中，可不拘于上述限制，也即图形的生成可按随机过程产生，也可按确定性模型生成[5]，由此Voronoi节理网络可分为不规则型(由随机过程产生)和规则型(由确定性模型产生)两类(图2)，可分别用于不同条件下岩体结构的模拟。

图2 Voronoi节理网络Fig.2 Voronoi joint net

Voronoi节理图的生成通常首先通过均匀分布在平面内(二维空间)产生一系列的“种子”点， 然后依据这些点(特征点)通过一定算法构建出Voronoi凸多边形。而产生的多边形为规则或不规则形状可由产生泊松点的过程来控制[5-6]。

1.3 Voronoi节理模型在岩体工程中的应用

尽管Voronoi图形在许多领域得到了广泛的应用，但在岩体工程中的应用研究到目前为止仍非常有限。文献[7]曾用Voronoi图形描述岩体的几何测量学形态，而文献[8]则采用该模型利用数值模拟研究了岩样在双向应力作用下裂纹扩展、破裂的过程，类似于PFC模型。除此之外，尚未见到更多该模型在岩体中的应用研究。

碎裂结构或镶嵌碎裂结构是指由多组结构面将岩体切割成块状、碎块状，因此用Voronoi图能够较好地描述碎裂岩体的特征，但是，由于实际中碎裂结构的节理裂隙分布特征及岩块大小等信息较难准确地获取，故在一定程度上制约了该模型的应用。尽管如此，该模型用于宏观上对碎裂岩体边坡或地基的评价仍具有一定前景。

碎裂岩体作为地基或岩石边坡工程，通常都是作为似均质体进行处理的，然而这种处理方法显然是粗糙的，尤其是对于碎裂岩边坡，不同的评价模型将会直接影响评价结果，包括斜坡的应力应变场、斜坡的破坏方式及最终的稳定系数估算结果等。基于此本文拟将Voronoi节理模型引入碎裂岩边坡的评价中，以其与均质体模型进行对比分析。

2 基于Voronoi节理模型的碎裂岩边坡稳定性分析

碎裂岩体是工程中常见的不良岩体。随着公路、铁路等工程建设的不断发展，修建在碎裂岩体中的边坡越来越多，其稳定性也已成为工程界非常关注的问题。特别是在地质条件复杂的山区，碎裂岩体边坡的稳定性问题更显突出。如川藏公路四川境内有很大一部分路堑边坡的坡体都是碎裂岩体[9]。目前对于碎裂岩体边坡稳定性的研究主要是针对设计和施工期间的稳定性分析和加固防护措施，而对于边坡的失稳机理研究工作做得相对较少。

碎裂岩体边坡的失稳破坏是一个复杂的过程。坡体内部的应力调整及结构面的剪切失效是坡体最终达到平衡的内在因素。外部各种诱发因素是加速坡体演化的动因。文献[10-11]分别考虑不同节理的组合形式对碎裂岩边坡进行了物理模拟和数值模拟分析，结果表明，碎裂岩边坡的破坏并不是一个瞬间的整体破坏过程，而是一个由局部破坏逐渐扩展以致贯通形成滑面的渐进破坏过程。除此外，以往大多数碎裂边坡研究中实际上都没有考虑节理裂隙对斜坡演化的控制作用， 这样就可能导致对边坡稳定状况的误判。

2.1 Voronoi节理模型有限元

Voronoi节理网络的生成如前所述，由于碎裂岩块通常都是不均匀、不规则的，因此模型中采用不规则形状的节理网络模型，根据野外碎裂岩块尺寸的大小，在模拟形成节理网络时，以单位面积的块体数量(密度)或平均节理长度来控制碎裂岩的破碎程度，以达到与实际接近的目的(图3)。同时，为了避免模拟区域尺寸对于Voronoi节理网格生成的影响，首先在更大的范围内随机产生均匀分布的“种子”点，生成Voronoi图后再通过模拟边界进行裁剪，得到最终的节理网络模型。

对斜坡模拟区进行离散化时，在所有节理(Voronoi凸多边形的边)都作为单元边界的基础上按要求进一步细化网格单元。

2.2 边坡模型及计算参数

某碎裂岩路堑边坡高度为20 m，岩性为三叠系中统变质砂岩，受风化、卸荷等影响，自坡面水平向里约20 m岩体破碎，不同方向结构面将岩体切割成直径约为70～90 cm的块状碎裂镶嵌结构，其中结构面一般微张，无充填，岩体为弱风化(上段)状态。为分析该边坡的变形破坏方式及稳定性，建立了两种有限元模型：其一采用传统的均匀连续介质模型，将碎裂岩体看作类似碎石土的材料进行处理，不考虑其中的节理；其二采用Voronoi节理模型，并赋以节理强度参数以模拟边坡的破坏过程。模拟分两组，一组边坡坡度为45°，另一组边坡坡度为40°，两组模型的材料相同。图4、图3分别为均质、Voronoi节理的有限元模型(两组模型只是坡度不同，所以只展示一组坡度为45°的模型图)，其中Voronoi模型所包含的节理设置为两端张开。

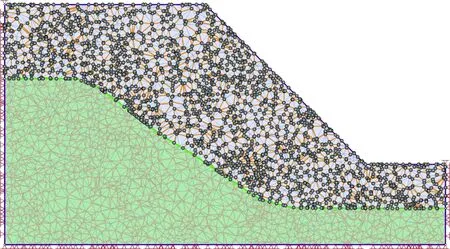
图3 碎裂岩边坡Voronoi节理有限元模型Fig.3 FEM model with Voronoi joint net

图4 碎裂岩边坡均质假设下有限元模型Fig.4 FEM model under the assumed condition of homogeneous medium

模拟中坡体物理力学参数取值相同。材料1是弱风化岩体，设置为塑性材料;材料2是未风化岩体，设置为弹性材料，且材料2中不设节理。计算时采用莫尔-库伦准则。各介质物理力学参数及节理物理力学参数列于表1和表2。

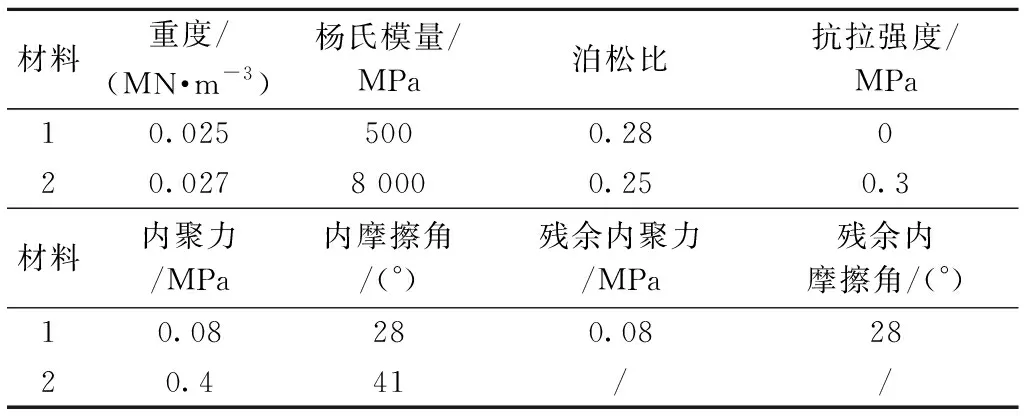
表1 边坡碎裂岩体物理力学参数

表2 边坡碎裂岩体节理力学参数

2.3 计算结果的比较分析

根据上述模型及物理力学参数取值，计算得到不同坡度时均质材料模型与Voronoi节理模型模拟计算得到的最大剪应变云图。

模型为40°边坡时，均质材料模拟结果与采用Voronoi节理法的模拟结果云图见图5和图6。

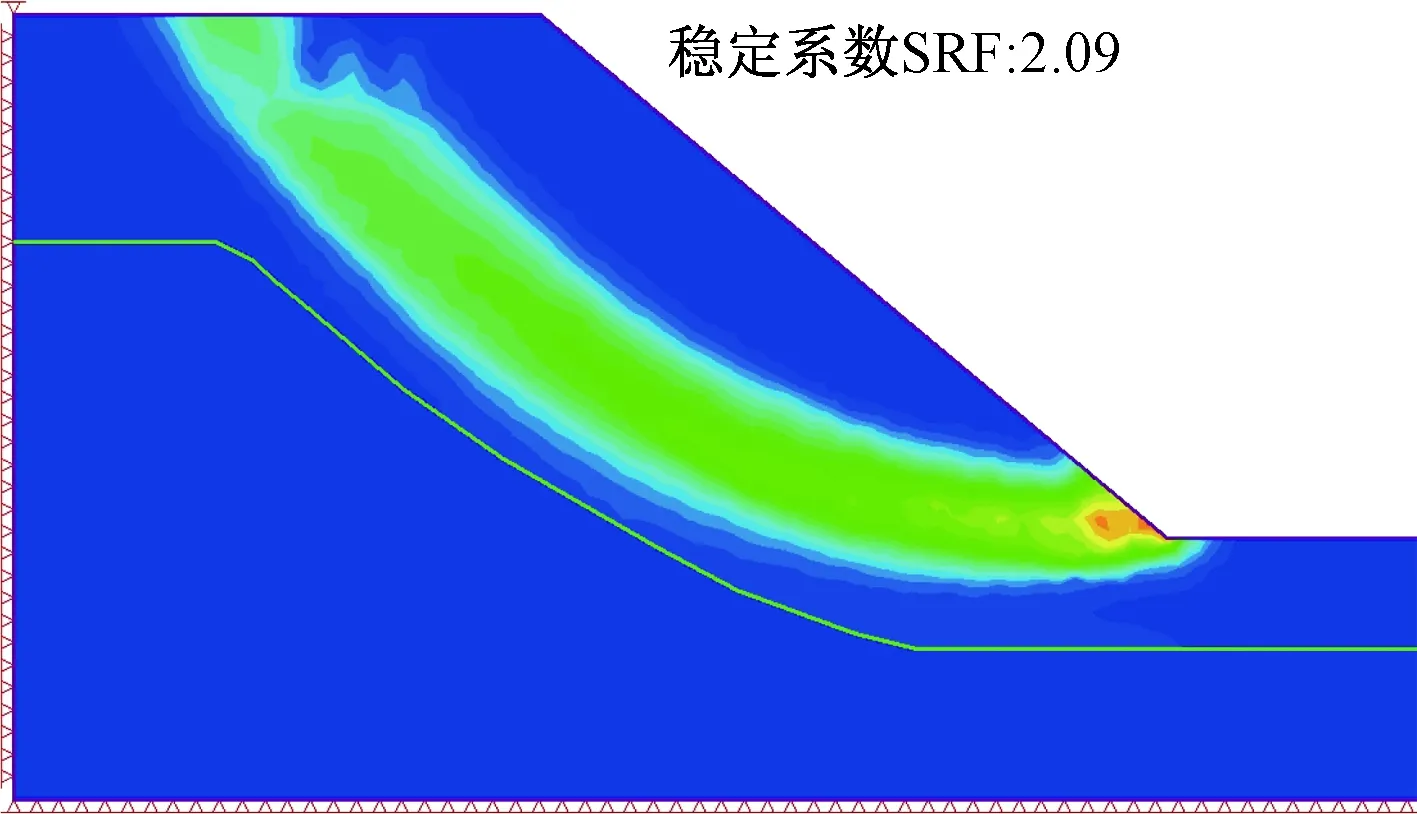
图5 均质材料模型模拟最大剪应变云图Fig.5 Maximum shear strain of uniform material

模型为45°边坡时，均质材料模拟结果与采用Voronoi节理法的模拟结果云图见图7和图8。

图7 均质材料模型模拟最大剪应变云图Fig.7 Maximum shear strain of uniform material

图8 Voronoi节理模型模拟最大剪应变云图Fig.8 Maximum shear strain of Voronoi joint model

上述采用Voronoi模拟方法的模拟结果与通常的均质体边坡模拟结果一致，其破坏方式为整体式的圆弧型滑动失稳；另外，两种模拟方法稳定系数相差不大。

2.3.1Voronoi节理模型与均质模型破坏过程

(1)Voronoi节理模型破坏过程见图9、图10。

图10 F=1.78时边坡总位移Fig.10 Total dispiacement (F=1.78)

(2)均质模型破坏过程见图11、图12。

图11 F=1.87时边坡总位移Fig.11 Total dispiacement (F=1.87)

图12 F=1.93时边坡总位移Fig.12 Total dispiacement (F=1.93)

由图9和图10可以看到采用Voronoi节理模型时，边坡最大位移位置首先发生在坡顶，并随着折减系数的增大，由坡顶向坡脚发展；由图11和图12可以看到均质模型首先在坡脚发生最大位移，并随着折减系数的增大逐渐向坡体内部发展为贯通的圆弧形破坏面。

2.3.2计算结果的比较分析

模型为40°边坡时，均质材料模型计算得到的稳定系数为2.09，采用Voronoi节理模型模拟计算得到的稳定系数为2.04；模型为45°边坡时，均质材料模型计算得到的稳定系数为1.9，采用Voronoi节理模型模拟计算得到的稳定系数为1.77。两种模型计算结果的差异反映在是否考虑边坡的结构性，即是否考虑节理在边坡中所起的作用。

对比两种模型的计算结果，可以得到下列结论：

(1)对于有多组节理发育且完全扰动的破碎岩体边坡，文中两种计算方法结果相近，但是采用Voronoi节理法得到的稳定系数偏小，在工程上属于偏安全。

(2)Voronoi节理法对边坡坡度的变化更敏感。当坡度从40°增大到45°时，采用均质材料模型得到的安全系数减小了9.09%，而采用Voronoi节理法得到的安全系数减小了13.24%。

(3)随着边坡坡度在一定范围内的增大，两种模型计算方法的结果稳定系数差异越大。当模型是40°边坡时，两者相差0.05；模型是45°边坡时，两者相差0.13。

(4)此类完全扰动的破碎岩体边坡，用Voronoi节理法进行模拟时，其破坏方式与一般均质体边坡一致，变形破坏基本不受节理控制。

3 Voronoi节理模型应用中存在的问题讨论

由于镶嵌碎裂岩边坡的结构特征极其复杂，且规律性较差，目前尚无较好的方法进行模拟。尽管离散单元法是针对节理岩体设计的，但要生成这类密集复杂的节理也非常困难。而Voronoi节理模型则能很好地从宏观上模拟这类结构，从而了解该类边坡的稳定状况和演化趋势。

然而，应用Voronoi节理模型时也存在如下一些问题：

(1)Voronoi凸多边形并不能完全真实反映碎裂岩块体的大小和形状(实际上这类岩体的真实情况也极难确定)，只能根据岩体的宏观块体特征进行模拟。

(2)根据Voronoi节理模型的特点，其适用于多组杂乱节理形成的镶嵌碎裂结构，而对于2～3组规律性较强的节理形成的碎裂岩体适用性值得进一步讨论。

(3)Voronoi模型计算结果云图表明，在此类边坡情况下其破坏方式与一般均质体边坡类似，节理面对边坡的安全基本不起控制作用，但计算结果在工程上偏安全。

4 结论

(1)相比于均质模型，Voronoi节理模型对边坡坡度的变化更为敏感。

(2)实例分析表明，利用均匀连续介质模型和Voronoi节理模型对同一边坡的模拟结果差异不大，破坏模式都是圆弧破坏剪切破坏，但后者的计算结果在工程上偏安全。

(3)两种模型破坏过程不同：Voronoi节理模型首先由坡顶开始产生最大位移，随后沿着坡面一定深度范围内向坡脚发展，而均质模型首先在坡脚产生最大位移，随后在坡体内部由下向上形成贯通的圆弧形破坏面。

(4)根据Voronoi节理模型自身特点，以及碎裂岩体结构本身确定的困难，该模型主要从宏观上对边坡状况进行模拟。

(5)本文只模拟了有多组节理的完全扰动的碎裂岩体边坡，对于规律性较强的节理化碎裂岩边坡应用Voronoi模型时，应进一步探讨。建议采用其它更适宜的节理模型进行分析。

参考文献：

[1] 张倬元, 王士天, 王兰生. 工程地质分析原理[R]. 北京：地质出版社，1994.

ZHANG Zhouyuan, WANG Shitian, WANG Lansheng. Engineering Geology Analytic Principle[R]. Beijing: Geology Press,1994.

[2] 李铁峰，潘懋，刘瑞珣. 基岩斜坡变形与破坏的岩体结构模式分析[J].北京大学学报(自然科学版)，2002, 38(2): 239-244.

LI Tiefeng, PAN Mao, LIU Ruixun.Analysis of the modes of rock mass structure on slope stability [J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2002, 38(2): 239-244.

[3] 于国辉, 李永鑫, 董万杰. Voronoi 图和它的偶图Delaunay镶嵌在数值分析中的应用[J]. 中国科技信息, 2005(15): 14-15.

YU Guohui, LI Yongxin, DONG Wanjie.The applications of Voronoi diagram and its dual-Delaunay tessellation in the numerical analysis [J]. China Science and Technology Information, 2005(15): 14-15.

[4] 余东晓, 颜钦武, 张正文，等.基于Voronoi网格技术的逐孔台阶爆破起爆顺序确定方法 [C]. 南京: 第一届全国工程安全与防护学术会议论文集,2008：611-616.

YU Dongxiao, YAN Qinwu, ZHANG Zhengwen, et al.Determination of initiation sequence for hole-by-hole blasting using Voronoi diagram [C]. Nanjing: Proceedings of the 1stNational Conference on Engineering Safety and Protection，2008: 611-616.

[5] Dershowitz W S, Einstein H H. Characterizing rock joint geometry with joint system models [J]. Rock Mechanics and Rock Engineering，1988,21: 21-51.

[6] 李志强. 利用Voronoi随机模型研究多孔材料的动态特性 [D].太原：太原理工大学,2008：31-38.

LI Zhiqiang.Study the dynamic crushing behavior of cellular materials by using the Voronoi random model [D]. Taiyuan:Taiyuan University of Technology,2008:31-38.

[7] Stoyan D, Kendall W S, Mecke J.Stochastic geometry and its applications[R]. Wiley: Chichester and N.Y.C.1987.

[8] Van de steen B, Vervoort A, Napier J A L. Numerical modelling of fracture initiation and propagation in biaxial tests on rock samples [J]. International Journal of Fracture,2001, 108: 165-191.

[9] 曹兴松. 碎裂岩体路堑高边坡失稳机理及防治技术研究 [D]. 成都：西南交通大学,2006: 1-8.

CAO Xingsong.Research on instability mechanism and controlling techniques for cutting high slope in disintegration rock mass [D]. Chengdu:Southwest Jiaotong University,2006: 1-8.

[10] 陈亚军, 王家臣, 常来山，等. 节理岩体边坡渐进破坏的试验研究[J]. 金属矿山，2005(8): 11-14.

CHEN Yajun, WANG Jiachen, CHANG Laishan, et al.Experimental research on progressive failure of jointed rock slope [J]. Metal Mine, 2005(8): 11-14.

[11] 陈亚军, 王家臣.节理岩体边坡渐进破坏的数值模拟研究[J].有色金属，2006,58 (2): 28-31.

CHEN Yajun, WANG Jiachen.Numerical simulation on progressive failure of jointed rock slope [J]. Nonferrous Metal，2006，58(2): 28-31.