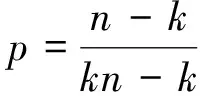关于Hamy平均的一个优化不等式

何晓红

(衢州广播电视大学 教务处,浙江 衢州 324000)

不加特殊说明, 都设

n∈N,n≥2,a=(a1,a2,…,an)n∈(0,+)n.

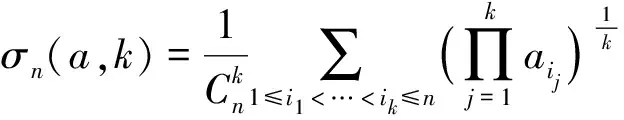
论文将研究关于n个正数的k次Hamy平均的双向优化不等式, 其系数具有最佳性.

1 有关引理

以下设集合D⊆Rn是有内点的对称凸集, 对于i=1,2,…,n, 记

引理1[6-7]设区间I⊆

若对引理1进行函数变换可得引理2, 详细证明参考文献[6-7].

引理2[6-7]设区间I⊆(0,+),为对称函数, 且有连续偏导数, 若不等式x1∂f/∂x1>(<)x2∂f/∂x2在上恒成立, 则对任意的a∈In, 都有等号成立当且仅当a1=a2=…=an, 其中：

证明设

H={lna=(lna1,lna2,…,lnan)|a∈In},g:y∈H→f(ey1,ey1,…,eyn),

则

引理3设k,n∈N且3≤k≤n,b2,b3,…,bn>0,且b2≤bi(3≤i≤n), 有

证明对n用数学归纳法, 当n=3时, 命题易知为真.假设命题对于n-1成立, 当n≥4时, 设

有

根据假设

有

所以,f(b2,b3,…,bn)关于bn是单调增加函数, 同理可证f(b2,b3,…,bn)关于bi(i=3,4,…,n)是单调增加函数, 有

引理3证毕.

2 主要结果

定理1设n,k∈N,n≥2,1≤k≤n,a=(a1,a2,…,an)n∈(0,+)n，a的k次Hamy平均为则

(1)

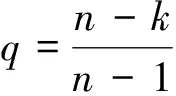
证明当n=2或k=1或k=n, 定理1显然为真. 下设n≥3.

(i) 在3≤k≤n-1情形下, 下面给出(1)式左式的证明.

设f:a∈(0,+)n→qAn(a)+(1-q)Gn(a)-σn(a,k), 则

根据对称性,有

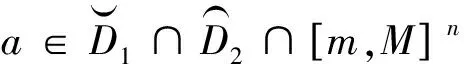
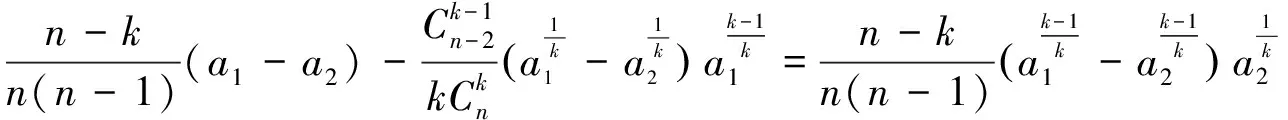
由引理2知, 对任意a∈(0,+)n, 都有即

σn(a,k)≤qAn(a)+(1-q)Gn(a)

成立.

(ii) 在3≤k≤n-1情形下, 下面给出(1)式右式的证明.

只要证

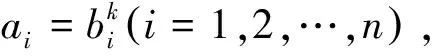
(2)

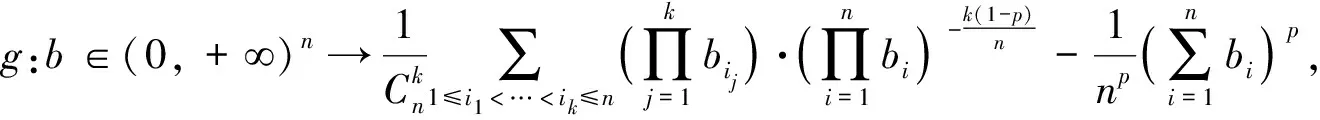
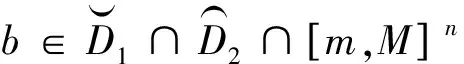
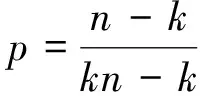
又因为

所以,只要证

⟺

(iii) 在k=2的情形下, (1)式等价化为

它的左右式证明分别类似以上两种, 而且在记法会简洁许多, 在此不再重复.

(iv) 下证q和p的最佳性.

取特例a=(1,1,…,1,t)(t>0,t≠1), (1)式的右式化为

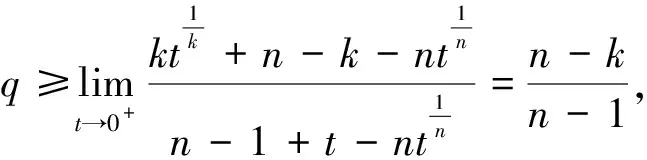
取特例a=(1,1,…,1,t)(t>0,t≠1), (1)式的左式化为

当t→+时, 比较上式t的最高次方, 有