基于流形降维和梯度提升树的大气腐蚀速率预测模型

梁喜旺，付冬梅，杨焘

（北京科技大学 自动化学院，北京 100083）

大气环境下的金属腐蚀作为一种常见现象，会造成严重的经济损失、安全隐患、资源浪费[1-2]，研究和掌握大气腐蚀规律具有重要的工程意义。大气腐蚀受到大气环境、金属化学成分含量和暴露时间等多方面因素影响，不同于基于腐蚀速率与环境因素关系的研究，预测新环境下特定材料的腐蚀行为，文中分析了特定大气环境下金属化学成分含量和暴露时间因素对大气腐蚀速率的影响，建立了腐蚀速率预测模型。

文中数据集具有高维、非线性且小样本的特点，化学成分对腐蚀速率的影响非常复杂，多达14种的化学元素影响程度各不相同，部分元素之间还存在相互作用的现象。由于样本种类有限，含有某些元素如铌、镭的金属比较少，这些特征变化不大，出现大量0值，带来了特征突变、数据冗余等问题，为建模预测带来困难。针对这些问题，文中首先对化学成分数据进行降维处理，得到更为约简、预测能力更强的特征。一般认为，腐蚀现象的发生是有一定条件的，各个化学成分之间存在一定形态的约束关系，这种约束关系决定了金属材料自身的耐腐蚀性。常用的主成分分析 PCA[3]是基于数据欧式距离全局结构的线性降维方法，可能会破坏数据间的非线性约束关系。流形方法[4]在保持数据全局或局部约束关系的同时，寻找一个映射子空间，使得降维后数据更加接近原始数据的非线性本质，比较具有代表性的有ISOMAP，LLE，LE等。等度规映射ISOMAP是多维尺度分析的拓展，尽量保持全局流形上两点距离不变；局部线性嵌入LLE在样本点和它的邻域点之间构造一个重构权向量，在低维空间中保持权值不变；拉普拉斯特征映射LE构造样本点之间的关联矩阵，并在重构低维嵌入时，保持高维空间中距离近的点在低维空间距离也近。上述流形方法虽然能实现高维数据的约简，却不能得到高维空间到低维空间的显式映射，降维处理只限于训练样本，难以应用到测试样本，此问题能通过引入线性化过程得以解决[5]。局部保持投影LPP是[6]LE算法的线性化算法，依据流形思想，保持局部信息，并得到高维数据到低维嵌入的线性映射。文中采用 LPP算法对金属化学成分进行降维处理，此外，为了较好地重构低维嵌入，提高局部保持能力，对LPP算法进行正交化改进。

LPP降维后的低维特征未与大气腐蚀速率建立联系，需要利用一定的建模方法实现腐蚀速率的预测。腐蚀速率预测领域常用的方法有灰色预测模型[7]、人工神经元网络[8]和CART回归树[9]等。典型的灰色GM(1,1)模型适合单一时序预测，难以引入金属化学成分的影响；神经元网络虽然能实现基于多个因素的预测，但需要大量样本和复杂的网络结构，且易于过拟合；CART回归树从单个特征入手，遍历所有特征，寻找最优划分特征和最优划分点，并在子空间重复划分，比较适合文中数据。单个回归模型结构简单，预测精度较低，容易出现过拟合现象，并对噪声敏感[10]。针对这些问题，文中采用梯度提升决策树算法。GBDT是近年来最有效的机器学习方法之一，是一种基于CART树的集成模型，最早由Friedman提出[11]，具有较好的健壮性和泛化能力，能有效提升预测准确性。同时，GBDT模型的可解释性比较好，能够分析影响腐蚀的关键因素。

文中主要利用 LPP算法挖掘了高维、非线性且小样本数据的本质特征，并结合 GBDT模型实现了大气腐蚀速率的预测，同时与几种典型预测模型进行对比研究。

1 LPP算法及正交化改进

LPP作为流形学习的重要分支，是一种典型的基于近邻图的降维方法，是拉普拉斯特征映射LE算法的线性化算法。为了方便表示，设原始数据集为低维嵌入为满足ℝD×d，为线性映射矩阵。LPP的目标是在寻找最优映射的同时，保持原始数据中的局部几何结构，通过k近邻法构建近邻图 G={ X, W }，若xi和xj互为近邻点，则通过热核函数为两点赋予连接权值，定义如式(1)所示。

式中：代表L2范数；t为热核参数。

LPP优化目标函数[12]：

式中：I为单位矩阵；D为对角线矩阵，为W 矩阵的行求和或列求和，即为拉普拉斯矩阵。为了得到唯一解，需要满足约束条件

由式(1)热核函数定义可知，原始高维空间距离较近的点之间具有较大的连接权值，因此，映射到低维空间中的点只有保持较近的距离才能使得目标函数达到最小。采用该方法计算的连接权值Wij保证了高维空间中处于近邻的数据点在低维空间中距离也很近。

显然，可以将式(1)改写成：

先考虑分子项

式中：tr(·)代表矩阵迹操作。令ei表示单位向量，第i个元素为1，其余为0，因此有：

展开括号内项，并重新合并项可得：

因此可得：

同理可得：

因此可将 LPP优化问题(1)转化成式(9)所示的矩阵迹之比形式。

通常来说，矩阵迹之比优化问题是非凸的，同时不存在闭式解，一般转化为更为简单的比值之迹形式[12]，如式(10)所示：

上式能够通过以下广义特征值问题求解：

A由式(11)的前d个最小特征值对应的特征向量组成。

LPP兼顾了局部最小映射和保持全局信息，但LPP得到的映射 A是非正交的，由式(3)和欧式距离定义，低维空间中yi和yj的距离可以表示为式(12)。可见，非正交的A在数据重构的过程中必然造成原始欧式空间结构不能完全被恢复。

通过正交化投影矩阵A，使得AAT=I，那么原始数据空间结构能被完全保持，局部信息损失降低。此外，降维后数据正交，特征区分度更高，有利于建模预测。文中采用一种基于QR分解的正交化LPP方法[6]。由式(10)可得出一个结论：若ˆA为它的一个最优解，则V也是它的一个最优解，V是任意可逆矩阵，因为：

QR分解是一种应用广泛的矩阵分解方式，将矩阵分解为正交矩阵Q和上三角矩阵R的乘积形式，对式(10)最优解进行QR分解：可得由上述结论可知也是优化问题(10)的最优解，并满足正交约束条件：A~A~T=I。

文中采用的正交化 LPP算法首先求解原始 LPP算法投影矩阵然后对进行QR分解，得到正交矩阵最终得到低维嵌入算法为非监督学习，低维数据集没有与腐蚀速率建立联系，需要借助回归模型实现腐蚀速率预测。

《易经》所提到的“天行健，君子以自强不息；地势坤，君子以厚德载物”，其意思是天（即自然）的运动刚强劲健，相应于此，君子处世，应像天一样，自我力求进步，刚毅坚卓，发愤图强，永不停息；大地的气势厚实和顺，君子应增厚美德，容载万物。中国几千年来所积淀的传统文化精髓告诉我们，不论是做人还是做事，都必须把“修身”“修德”作为人生的第一课。“自强不息、厚德载物”这也是做人应该具备的态度、胸怀与品格。

2 GBDT模型

梯度提升决策树（GBDT）是一种提升算法，其原理是将大量简单CART树在提升过程中进行集成，以提高树模型的预测能力。由于基于决策树算法，GBDT具有较好的模型可解释性[13]，为分析腐蚀影响因素的重要性提供了一种方法。

2.1 GBDT基本算法

假设输入训练样本集为：为了寻找回归树的最优组合，在每次迭代过程中顺序添加新的回归树来减少预测误差，新加入的回归树建立在之前所有树的负梯度之上。

估计函数f(x)预测y的损失函数L(f)定义为：

在回归问题中，一般为平方误差损失：

在梯度提升框架 M 次迭代中，全局函数估计( x)可以由加法模型表示：

其中，f0(x)为初始值，定义为：

在迭代次数中，对样本i=1,2,3,…,N计算负梯度：

利用拟合一棵 CART回归树，得到第 m棵树，其对应的叶子节点区域为为回归树m的叶子节点个数。对叶子区域计算最佳拟合值，并更新强学习器：

η的取值范围为：0＜η≤1。对于同样的训练集学习效果，较小的η需要更多的迭代次数，即回归树的总棵数；较大的η容易出现过拟合，通常同时调节迭代次数和学习率来决定模型的预测性能。

2.2 GBDT的模型可解释性

在腐蚀速率预测中，模型的可解释性十分重要，GBDT模型通过计算特征重要性来分析影响腐蚀的关键因素，Friedman在GBM论文中[12]提出的方法：

设特征总数为D，特征的全局重要性通过特征在单个树中的平均值来衡量：

式中：M是树的数量；Tm为第 m棵树。特征 d在单棵树中的重要性为：

式中：J为树的叶子节点数量；vj是和节点j相关联的特征；是节点j分裂后平方损失的减少值；为示性函数，当vj与特征d相关联时，示性函数值为1，否则为0。

3 实验结果与分析

3.1 数据集准备和分析

文中采用数据来源于中国腐蚀与防护网黑色金属大气腐蚀数据库青岛腐蚀站点数据，包含了暴露时间、碳、硅、锰、硫、磷等共14种化学元素含量参数和实验金属的腐蚀速率，共16种实验金属，80个样本，部分腐蚀速率数据见表1。对于每一个站点而言，每年的平均环境因素变化不大，为了便于分析，可忽略环境因素影响，分析特定站点下的金属合金元素含量和暴露时间对腐蚀的影响。

3.2 预测性能评估方法

文中采用平均绝对误差MAE和平均绝对百分误差 MAPE来评估模型的预测效果。平均绝对误差MAE计算预测值和实际值之间偏差绝对值的平均，计算公式为：

为了评估预测误差相对于实际值的大小，还采用了平均绝对百分比误差MAPE，计算公式为：

式中：N为样本数量；y为实际值；为模型预测值。

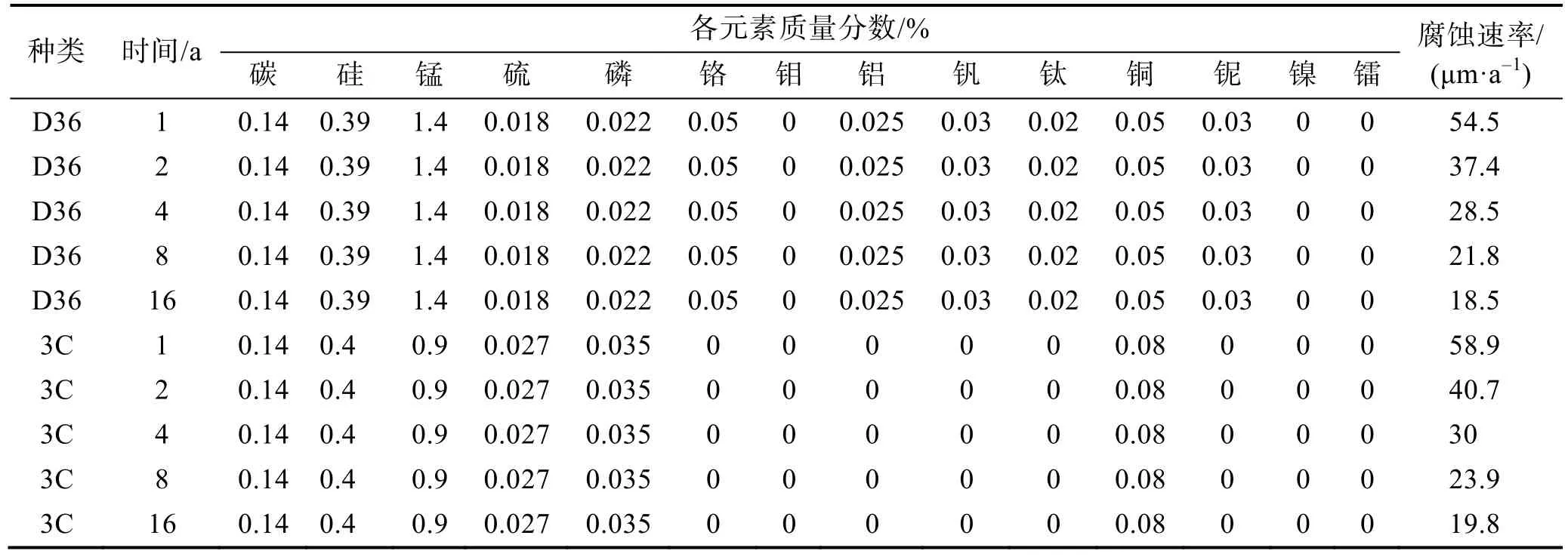
表1 青岛腐蚀站点部分数据

3.3 模型建立过程

LPP-GBDT预测模型分为两部分，第一步利用LPP对金属化学成分数据进行降维处理，第二步利用低维数据训练 GBDT模型，实现腐蚀速率的预测。该模型需要调节的参数共有 5个，分别为 LPP算法的目标维数d、近邻点个数k、热核函数参数t、GBDT算法的迭代次数（回归树数量）M、学习率η。考虑到时间开销和计算机性能，分两步优化参数，采用留一法交叉验证，以 GBDT预测的平均绝对误差作为评价标准。

以确定LPP参数为例，首先将GBDT模型参数固定为M=100，η=0.1，优化LPP算法3个参数。参数区间设置为：d为区间[2,13]内的整数；k为区间[2,27]内的整数；t为区间[0.05,2]内的浮点数，步长为0.05。同时搜索了效果对比方法PCA的参数，参数优化结果见表2。

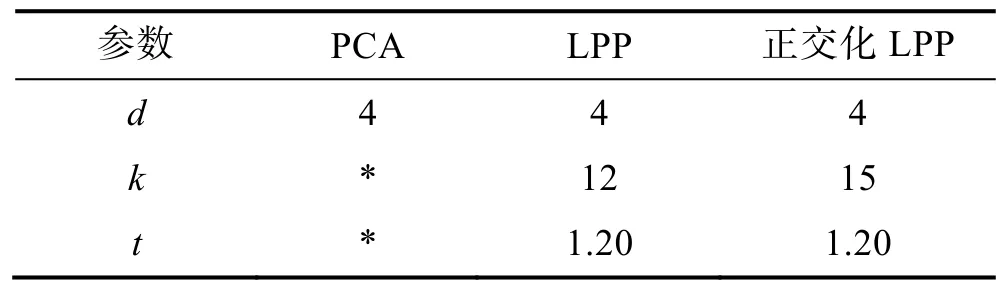
表2 参数优化结果

LPP算法降维处理可以视为一个特征重构的过程，LPP降维结果如式(26)—(29)所示，其中，Featurei（i=1,2,…,4）表示构造的低维特征：

从降维结果可以看出，金属化学成分数据集通过不同的降维方法降至4维具有较好的预测能力，说明此数据集的本征维数极有可能为4维，需要更多后续研究加以验证。

在获得LPP参数后，优化GBDT参数，区间设置为：M为区间[30,1000]内的整数，以10为步长；学习率η分别取 0.01，0.03，0.05，0.1，结果如图 1所示。可以看出，训练集误差随回归树数量的增加而降低并趋于不变，降低速度随η的增加而变大。当η比较大时，测试集很快出现过拟合现象；若η太小，则需要较多的基学习器个数（M）。结合训练、测试误差及模型复杂度综合考虑，确定GBDT的参数为：M=600，R=0.03。

3.4 预测模型性能检验

为了验证文中建立模型的预测性能和泛化能力，随机选取4种金属的共20个样本作为测试集，其余60个样本作为预测模型训练样本，采用留一交叉验证训练模型参数。基于原始数据，不同模型预测结果见表3。其中，SVR支持向量机非线性回归，核函数为RBF，惩罚系数C=10，松弛变量ξ=0.1。ANN为多层感知器模型，设置3层网络，迭代次数为600。CART回归树取50次实验结果平均值。

通过单个模型仿真结果看出，实验采用的单个模型的预测效果普遍较低，训练误差和测试误差都比较大。几种模型相比而言，CART回归树的预测误差较低，比较适合本文数据集建模。通过梯度提升算法的引入，建立多棵回归树，GBDT极大地提升了单棵CART回归树的预测效果，预测误差降低近一半。

为了进一步提高 GBDT的预测性能，采用 LPP和正交化 LPP算法对原始数据进行降维处理，为了验证LPP方法降维的有效性，采用PCA算法作为参考，仿真结果见表4。

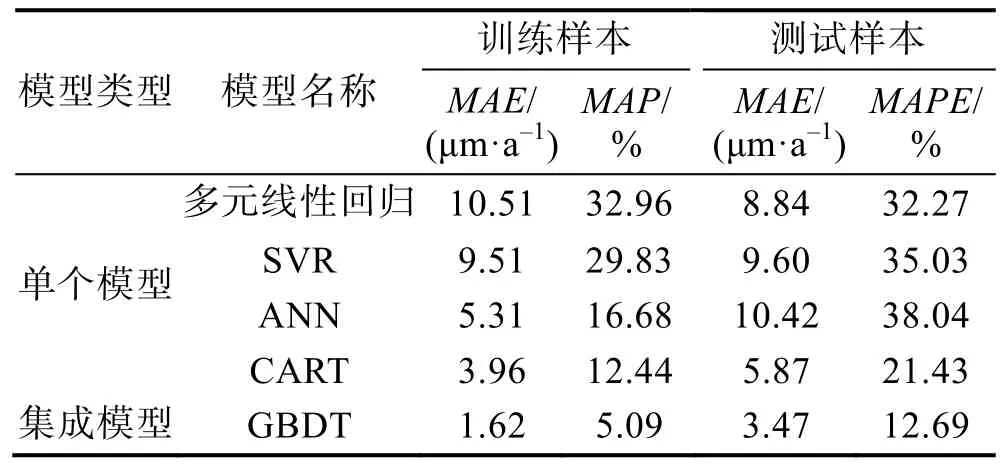
表3 基于原始数据模型预测性能对比

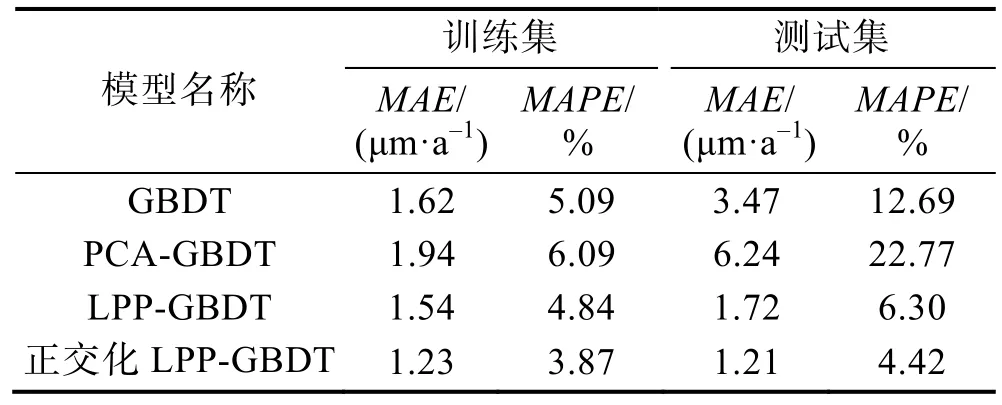
表4 基于降维数据模型预测性能对比

相比于基于原始数据建立的GBDT模型，PCAGBDT的训练误差变化不大，但测试误差几乎提高了1倍，模型的泛化能力大大降低。可见，PCA的线性降维过程破坏了金属化学成分之间的复杂非线性关系。采用LPP算法降维GBDT模型的训练、测试误差都降低，拟合和泛化能力明显提升，预测性能明显改善。其中正交化 LPP-GBDT取得了最低的测试误差，比原始数据GBDT提高近8%，验证了LPP方法构造的简约化特征具有更高的回归预测能力，同时也验证了正交化处理在提高局部能力和增加数据区分度方面的优势。

3.5 腐蚀速率影响因素重要性分析

GBDT是解释性比较好的模型，对原始数据集建模预测时，通过2.2中所述方法对模型进行分析，各影响因素重要性结果见表5，特征重要性合计为 1，平均值为0.0667。

表5 影响因素重要性排序

可以看出，暴露时间是影响大气腐蚀速率的主导因素，在金属化学成分中，硫、碳、磷、铜、钼、钒、锰的影响比较大，其中硫、磷、铜的重要性符合相关文献的描述[14]，硫、碳降低金属的耐腐蚀性，磷、铜、锰增强金属的耐腐蚀性。青岛站点为典型的海洋大气环境，大气中海盐粒子较多，钼有利于防止氯离子的存在所产生的点蚀倾向，钒具有耐酸、耐盐的特性，因此钼和钒具有较高的特征重要性。硅通常被认为具有增强耐腐蚀性的作用，能促进耐腐蚀的稀土元素的富集[15]，但实验结果却没有印证这一结论，原因可能是本文样本中含稀土元素的金属极少，或硅在湿热的大气环境下的作用更为明显[14]。此外，由于样本金属材料的种类限制，一些合金元素对腐蚀速率的影响不是很明显，需要扩充样本种类作进一步研究。

4 结论

1）针对高维、非线性和小样本数据集，通过与其他典型方法的比较，GBDT取得了较好的预测效果，并分析了众多因素对于腐蚀速率的影响程度，为特定环境下金属材料的合金元素的调整提供一定的参考。

2）LPP及其正交化改进方法能有效处理高维非线性数据，线性重构简约化特征。实验结果表明，LPP算法的引入进一步提升了GBDT的预测性能。

3）文中建立的LPP-GBDT模型不仅适用于青岛腐蚀站点腐蚀数据，还可推广到其他大气环境下的腐蚀速率预测。

[1]LI X, ZHANG D, LIU Z, et al. Materials Science: Share Corrosion Data[J]. Nature, 2015, 527(7579): 441.

[2]高蒙, 孙志华, 刘明, 等. 7B04铝合金在 NaCl沉积与SO_2环境下的大气腐蚀行为[J]. 环境技术, 2016,34(5): 9-13.

[3]JOLLIFFE I T, CADIMA J. Principal Component Analysis: A Review and Recent Developments[J]. Philosophical Transactions, 2016, 374(2065): 20150202.

[4]IZENMAN A J. Introduction to Manifold Learning[J].Wiley Interdisciplinary Reviews Computational Statistics,2012, 4(5): 439-446.

[5]WANG R, NIE F, HONG R, et al. Fast and Orthogonal Locality Preserving Projections for Dimensionality Reduction[J]. IEEE Transactions on Image Processing, 2017,PP(99): 1.

[6]HE X, NIYOGI P. Locality Preserving Projections[J].Advances in Neural Information Processing Systems,2004, 16(1): 186-197.

[7]黄海军, 李婵, 王俊. 典型大气腐蚀介质的灰色预测模型分析[J]. 装备环境工程, 2012, 9(1): 13-16.

[8]邓志安, 李姝仪, 李晓坤, 等. 基于模糊神经网络的海洋管线腐蚀速率预测新方法[J]. 中国腐蚀与防护学报,2015, 35(6): 571-576.

[9]BRIAN R. Tree: Classification and Regression Trees[J].Wiley Interdisciplinary Reviews Data Mining &Knowledge Discovery, 2016(1): 14-23.

[10]CHOU J S, NGO N T, CHONG W K. The Use of Artificial Intelligence Combiners for Modeling Steel Pitting Risk and Corrosion Rate[J]. Engineering Applications of Artificial Intelligence, 2016, 65: 471-483.

[11]FRIEDMAN J H. Greedy Function Approximation: A Gradient Boosting Machine[J]. Annals of Statistics, 2001,29(5): 1189-1232.

[12]ZHANG L, QIAO L, CHEN S. Graph-optimized Locality Preserving Projections[J]. Pattern Recognition, 2010,43(6): 1993-2002.

[13]YANG S, WU J, DU Y, et al. Ensemble Learning for Short-term Traffic Prediction Based on Gradient Boosting Machine[J]. Journal of Sensors, 2017(4): 1-15.

[14]梁彩凤, 侯文泰. 钢的大气腐蚀预测[J]. 中国腐蚀与防护学报, 2006, 26(3): 129-135.

[15]陶鹏, 孙金全, 董彩常, 等. 海洋大气环境中含稀土耐候钢暴露1年的耐蚀性能研究[J]. 装备环境工程, 2017,14(5): 21-24.