改进的双种群遗传算法在矩形件排样中的应用

孙佳正，郭 骏

华东师范大学 计算机科学与软件工程学院，上海 200062

1 引言

矩形件排样优化问题是指把一定数量的矩形件排放到矩形板材上，在排样后矩形件之间不能重叠且矩形件不能超出板材的边界条件下，使得矩形板材的利用率尽可能的高。矩形件排样优化问题常见于制造业中，例如玻璃、布料，钢材切割等场景，关系到生产中材料的利用率，具有较高的经济价值与研究价值。此问题是NP完全组合优化问题，在大规模矩形件排样问题中，由于计算复杂度大，难以在短时间内找到最优解，因此一般研究方向是寻找启发式算法寻找接受的较优解。

矩形件排样优化问题一般可以分为排序和排放两个步骤，即确定矩形件排放的先后顺序和矩形件在板材中的排放方式，然后按照给定的排放方式，按顺序逐个排放矩形件。早期生产中由人工排样，耗时长，材料利用率低，增加了企业的生产成本。20世纪90年代以来，随着计算机的兴起，国内外学者从智能优化的角度对计算机辅助排样进行相关研究，一般采用启发式算法对排放顺序进行寻优，例如遗传算法[1-2]、模拟退火算法[3-4]、蚁群算法[5]等。在排放算法方面提出了BL排样算法，最低水平线排样算法。

Baker[6]提出BL排样算法，按照最左最下的规则排放矩形件。Jakobs[7]采用遗传算法求解排序，并采用与BL排样算法相结合的方式解决矩形件排样问题。针对BL排样算法易产生矩形件倾斜的缺陷，Liu[8]提出了一种改进的BL算法，向下向左移动矩形件时，优先向下移动，并与遗传算法结合起来解决矩形件排样问题。Soke[9]分别将遗传算法、模拟退火算法与改进的BL排样算法进行结合并对比排样效果。贾志欣[10]提出最低水平线排样算法，即在最低高度的水平线上靠左排放矩形件。龚志辉[11]提出了最低水平线搜索算法，当最低水平线的宽度小于待排矩形件，向后搜索一个小于最低水平线的宽度的矩形件，然后交换这个矩形件与当前待排矩形件的排放顺序。Liu[12]提出分阶段遗传算子来改进遗传算法，当遗传陷入停滞时，改变遗传算子来跳出局部极值，并与最低水平线排样算法结合起来处理矩形件排样问题。刘海明[13]结合了分阶段遗传算子与最低水平线搜索算法。

本文主要工作：结合了遗传算法与最低水平线搜索排样算法，即利用遗传算法对排放顺序寻优，使用最低水平线搜索排样算法排放矩形件，并分别加以改进。（1）传统的遗传算法采用一般的交叉方法在大规模离散空间内随机搜索最优解时容易出现收敛速度慢，陷入局部极值，稳定性差等问题。针对此缺陷，引入部分按照面积大小排序的个体以达到加速收敛的目的。因为在生产中工人单纯地按照矩形件面积大小的顺序排样通常比随机顺序排样效果好。然而在同一种群中，这部分个体比随机个体适应度高，迭代前期快速扩散，使得种群多样性降低，导致遗传算法过早熟。采用双种群策略对遗传算法的初始种群进行优化，一个种群按照矩形件面积从大到小的排序生成，另一个种群随机生成。按照矩形件面积从大到小的排序生成的种群通过特定交叉方式与随机初始化的种群进行基因交流，并保证子代个体大体上按照面积大小排序局部乱序，大体有序的基础上在解空间内进行搜索。（2）最低水平线搜索排样算法的改进：传统的最低水平线搜索排样算法只有在最低水平线的宽度小于待排矩形件的宽度时才会向后搜索合适的矩形件排放在最低水平线上。为增加搜索发生的时机，改进后的算法可以在排样的同时启发式判断在未排放的矩形件中是否有更合适的矩形件可以替换当前要排放的矩形件。更加频繁地动态调整矩形件的排放顺序，相当于增强了遗传算法的局部搜索能力。

2 矩形件排样问题的描述

在不同的生产环境下，矩形件排样问题描述可能有所不同，此问题一般化语言描述：给定一组长度宽度已知的矩形件，将它们排放到宽度固定，高度不限的矩形板材上，满足要求：（1）矩形件之间不能重叠。（2）矩形件不能超出板材边界。（3）矩形件可以90°旋转后排放，排放后矩形件的底边与板材底边平行。矩形件排样问题的目标是求出达到板材利用率最大的排样方案。其中板材利用率的定义为这组矩形件面积之和与耗用板材材料面积之比。

矩形件排样问题数学语言描述：设矩形板材的底边宽度为W，n个矩形件(p1,p2,p3,…,pn)，第i个矩形件pi的宽度为wi，高度为hi，排放后左下角的横坐标与纵坐标为xiyi。

H为n个矩形件排放完成后，所有矩形件上边距离板材底边的最大高度，如图1所示。E为板材的利用率：矩形件面积之和与耗用板材材料面积之比。

图1 所有矩形件上边距离板材底边的最大高度

矩形件排样优化问题可描述为，满足约束条件的同时，求解板材最大的利用率式（1）的最佳排样方案：

且满足约束条件：

（1）矩形件排放后不超出板材边界。

（2）排放后的矩形件互不重叠。

3 最低水平线启发式搜索排样算法

龚志辉[11]提出最低水平线搜索排样算法，排样规则是在最低高度的水平线上靠左排放矩形件，如果高度最低的水平线有多条，在最左边的一条排放矩形件。当排放不下当前待排放矩形件时，向后搜索一个小于最低水平线的宽度的矩形件，然后交换这个矩形件与当前待排矩形件的排放顺序。找不到合适的矩形件时，提升最低水平线的高度到与之相邻水平线中较低的一条的高度，合并高度相同的水平线，每次提升最低水平线时都会形成无法利用的空洞。赵新芳[14]在此基础上提出基于最低水平线的择优搜索，向后搜索能排放到最低水平线上宽度最大的，并且插入到当前待排放矩形件之前排放而不是交换排放顺序，为了防止大尺寸矩形件累积到后面排放。

然而传统的最低水平线搜索排样算法只有在最低水平线的宽度小于待排矩形件的宽度时才会向后搜索，搜索的频率低，调整排样顺序的机会少。本文提出的最低水平线启发式搜索排样算法可以在排样的同时进行搜索，启发式判断是否有更合适的矩形件排放在当前位置。

3.1 最低水平线搜索排样算法改进处理

本文改进后的算法在当前矩形件排放在最低水平线上后，最低水平线的剩余宽度无法继续排放任何未排放的矩形件时包括剩余宽度为0的特殊情况，判断在未排放的矩形件中是否有更合适的矩形件可以替换当前矩形件，更加频繁的动态调整矩形件的排放顺序。改进的最低水平线排样过程如下：

（1）初始化水平线的集合，当前只包含一条水平线，即板材的底边。初始化排放顺序，按照顺序逐个排放矩形件。

（2）在水平线集合中找到高度最低的水平线，如果有多条，选择最左的一条。对当前待排矩形件 pi，判断是否可以排放到最低水平线上，如果可以转入步骤（4）。如果不可排放，转入步骤（3）。

（3）向后搜索未排放的矩形件，找到的第一个可以排放到最低水平线上的矩形件 pj，把搜索到的矩形件 pj作为当前要排放矩形件，原待排放矩形件 pi作为下一个等待排放的矩形件，转入步骤（4），如果找不到转步骤（5）。

（4）最低水平线宽度减去待排放矩形宽度作为剩余的最低水平线，在排放矩形件之前向后搜索未排放矩形件中有没有矩形件能继续排放到剩余的最低水平线上，如果有，转入步骤（5）。如果没有，则在所有未排放的矩形件中寻找可以排放在最低水平线上，宽度最大的矩形件。如果有多个，则选择最高的矩形件 pm，并与当前待排放矩形件交换排放的顺序。

（5）在最低水平线上靠左排放当前矩形件。更新水平线集合，选择下一个待排放矩形件，转入步骤（2）。若所有矩形件都排放完毕，结束。

（6）升高最低水平线到与之相邻水平线中较低的一条的高度，合并相同高度的水平线，更新水平线集合，转入步骤（2）。

改进后的最低水平线排样算法可以更加频繁的动态调整矩形件排放的顺序，相当于弥补遗传算法局部搜索能力不足的缺陷，同时尽可能地利用板材的空间。改进的最低水平线排样算法流程如图2所示。

3.2 最低水平线启发式搜索排样算法原理

改进的原理是排样时先排放大的矩形件，后排放小的矩形件。大的矩形件排放时产生的空洞，可以用小的矩形件来填充。

当前等待排放的矩形件排放后，最低水平线剩余的宽度无法继续排放任何未排放的矩形件时，传统的最低水平线搜索排样算法会提高最低水平线，形成无法利用的空洞。本文改进的算法在这种情况下可以在所有未排放的矩形件中寻找可以排放在最低水平线上，宽度最大的矩形件 pm，并与当前待排放矩形件交换排放的顺序，尽可能地利用最低水平线的宽度。交换排放顺序目的是让大矩形件先排放，小的矩形件后排放。

图2 改进的最低水平线排样算法流程图

传统的最低水平线搜索排样算法按顺序排放矩形件{p1p2p3p4p5p6},p1p2p3p4排放后如图3所示，传统的最低水平线搜索算法排放p5后最低水平线无法继续排放p6，因此会升高最低水平线，形成没有利用的黑色的空洞，造成材料的浪费，如图4所示。图5为改进后的算法，当要排放矩形件 p5时，改进后的算法会检测到最低水平线上剩余的宽度无法继续排放矩形件 p6，然后寻找到未排放矩形件中宽度最大的矩形件p6与矩形件p5交换排放顺序。

图3 p1p2p3p4排放后

图4 最低水平线搜索排样

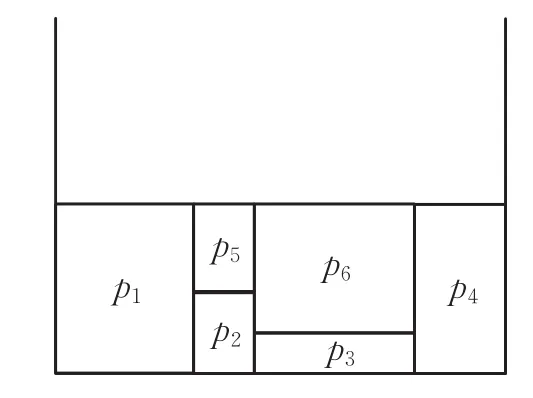
图5 最低水平线启发式搜索排样

传统的最低水平线搜索排样算法按顺序排放矩形件{p1p2p3p4p5p6}，p1p2p3p4排放后如图6所示，传统的最低水平线搜索算法排放会按顺序排放p5p6，如图7所示。图8为改进后的算法，当要排放矩形件 p5时，改进后的算法会检测到最低水平线上剩余宽度为0，然后寻找到未排放矩形件中宽度与 p5相同但高度比 p5高的的矩形件p6，与矩形件p5交换排放顺序。

图6 p1p2p3p4排放后

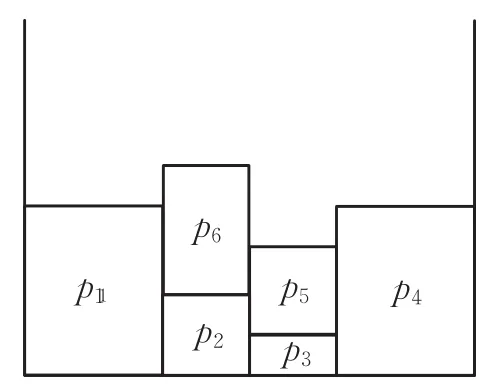
图7 最低水平线搜索排样

图8 最低水平线启发式搜索排样

4 改进的双种群遗传算法

矩形件的排样结果和矩形件的排放顺序紧密相关，本文使用遗传算法作为排样顺序问题的求解：遗传算法模拟自然界生物的进化过程，生物在繁衍的过程中染色体会交叉变异，经过种群适者生存优胜劣汰后，逐代产生更加优秀的个体，从而实现解的优化。排样优化问题属于多目标优化问题，解空间是离散的，而遗传算法可以从多个点出发寻找最优解，具有优秀的全局搜索能力，适合寻找大规模离散优化问题中的解。

由于排样问题的解空间是离散的，劣质解附近可能会存在优秀解，对此蒋兴波[15]与杨卫波[16]用遗传模拟退火算法弥补传统遗传算法局部搜索能力不足的缺陷。

传统的遗传算法中随机生成初始种群，容易造成排样结果时好时坏，稳定性差。未利用有效信息，在人工排样的过程中，熟练的工人单纯的按照矩形件面积从小到大排样往往可以取得不错的效果。同时，传统的遗传算法在大规模离散空间内随机搜索，容易造成收敛速度慢和陷入局部极值进而收敛停滞。

4.1 双种群遗传算法相关处理

在遗传算法的随机初始的种群中加入部分按照面积大小排序的个体以达到加速收敛的目的。如果在同一个种群中，这部分个体比随机个体适应度高，迭代前期不易被淘汰反而快速扩散，使得种群多样性降低，导致遗传算法过早熟。本文提出把随机生成的个体作为一个种群，按照面积大小排序生成的个体作为另一个种群并采用与随机初始化的种群个体交叉进行迭代，并且通过特定的交叉方式，保证子代的排放顺序为面积较大的矩形件最先排放，面积较小矩形件最后排放，达到大体上有序局部乱序的目的。

4.1.1 遗传算法个体编码方式及适应度函数

遗传个体的编码方式：由于目的是得到矩形件的排放顺序，直观起见，本文采取十进制整数的编码方式，从1开始，对每个矩形件按照顺序编号，由编号组成的序列表示矩形件的排样顺序，并且符号位表示是否旋转，正值表示不旋转，负值表示90°旋转矩形件。例如排样序列（－3，1，2）表示先把第3号矩形件旋转90°排放，然后再排放1号矩形件，最后再排放2号矩形件。

适应度函数：采用上文提出的最低水平线启发式搜索排样算法排样后的板材的利用率作为适应度的值，板材的利用率为矩形件面积之和与耗用板材材料面积之比，其取值范围为0到1，板材的利用率越高，表示排样效果越优秀。

4.1.2 种群A遗传过程

本文采用双种群遗传算法，第一个种群A遗传过程如下：

初始种群：本种群的初始个体是随机的，即产生随机序列，随机方向，数量为m1个个体。

选择方式：直接保留优秀个体，设选择算子为 psA，0＜psA＜1，将个体按照适应度从大到小排序，前 psAm1个的直接保留到下一代。

交叉方式：采用两点环形交叉方式[17]，设交叉算子为 pcA，0＜pcA＜1，产生 pcAm1个个体。两点交叉的过程为：产生两个不相等的，取值范围为1到n随机正整数ab为交叉点位置，n代表排样序列的长度。种群中随机抽取父代S1，S2。

如果a＜b，a位置到b位置之间的基因继承自S1，其他基因继承自S2，即保持在S2中的顺序和方向。例如表1中交叉点位置为a=3，b=5时染色体交叉情况。

表1 染色体交叉案例

如果a＞b，1到b区间，a到n区间的基因继承自S1，其他基因继承自S2，即保持在S2中的顺序和方向。例如表2中交叉点位置为a=6，b=2时染色体交叉情况。

表2 染色体交叉案例

变异操作：可分为旋转变异和交换变异。旋转变异指把某个矩形件旋转90°，交换变异指把两个矩形件的排放顺序进行交换。设旋转变异算子为 pm1A，0＜pm1A＜1，交换变异算子 pm2A，0＜pm2A＜1，分别产生pm1Am1和 pm2Am1个个体。

为保证每代个体数目不变，满足条件：

种群A迭代一定次数结束后，产生第二个种群B。

4.1.3 种群B遗传过程

初始种群：按照面积从大到小，方向随机产生数量为m2个个体。

选择操作：直接保留优秀个体，设选择算子为 psB，0＜psB＜1，将个体按照适应度从大到小排序，前 psBm2个的直接保留到下一代。

交叉操作：设交叉算子为 pcB，0＜pcB＜1，产生pcBm2个个体。与上一个迭代结束后的种群A进行两点交叉操作：产生随机不相等正整数ab为交叉点位置，且a＜b，a和b的取值范围为1到n，n代表排样序列的长度。父代S1从种群B中随机抽取，父代S2从迭代完成后的种群A中随机抽取，交叉的过程为1到a，b到n区间的基因继承自S1，其他基因继承自S2即保持在S2中的顺序和方向，例如表3中交叉点位置为a=2，b=6时染色体交叉情况。

变异操作：可分为旋转变异和交换变异。旋转变异指把某个矩形件旋转90°，交换变异指把两个矩形件的排放顺序进行交换。设旋转变异算子为 pm1B，0＜pm1B＜1，交换变异算子 pm2B，0＜pm2B＜1，分别产生pm1Bm2和 pm2Bm2个个体。

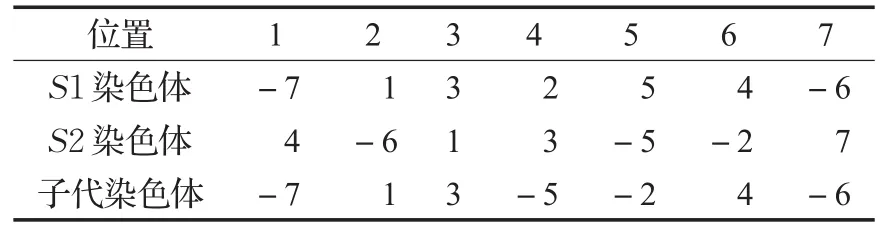
表3 染色体交叉案例

为保证每代个体数目不变，满足条件：

种群迭代一定次数，取两个种群的最优解。改进的遗传算法过程如图9所示。

图9 改进的遗传算法过程

4.1.4 种群内相似度计算

统计个体X，Y之间的编码同一位置处相同的矩形件编号的个数之和公式：

个体X，Y相似度计算公式：

其中n是染色体长度，当XY同一位置对应的矩形件的编号相同时，k=1，否则k=0。

种群P内部相似度计算公式：

m代表种群P中个体总数，PiPj代表种群中的不同个体。种群内相似度越高，代表种群内多样性越低。

4.2 双种群遗传算法改进原理

双种群遗传算法改进的思路：种群A初始值随机产生，采用两点交叉法可以增强遗传算法在离散解空间的搜索能力，在迭代停止后种群A隐含了矩形件之间排放顺序的优先级信息。

表4 矩形件描述信息

种群B是按照矩形件面积从大到小排序生成，原理是从早期人工排样的经验得知，单纯的按照矩形件从大到小的顺序排放矩形件能得到不错的板材利用率，种群B可以保证排样效果的稳定性。

种群B的交叉方式为先按照面积大小排序矩形件，然后在序列中间的矩形件的顺序继承自迭代完成后种群A，原理是开始时排放大矩形件，最后排放小矩形件，因为当大矩形件排放后出现的空洞可以用后面未排放的小矩形件填充，中间位置矩形件的排放顺序参照种群A的迭代结果，利用了种群A迭代后的隐藏信息：矩形件之间排放顺序的优先级。这样可以在种群B初始适应度不错的基础上有效利用了种群A迭代后的隐藏信息，保证了排样的效果的基础上更加有效的搜索最优解。

种群B采用特定的交叉方式，保证子代中面积较大的矩形件最先排放，面积较小矩形件最后排放，在大体有序的基础上搜索最优解，更有方向性和目的性。

将随机个体与有序个体分成两个种群，也避免出现迭代过程中由于种群中随机个体数目减少导致种群多样性降低，从而引发收敛停滞的问题。

本文的双种群遗传算法充分结合了遗传算法的全局搜索能力与先排放大矩形件后排放小矩形件的原理，可以有效改善传统遗传算法的搜索效率低及过早收敛，稳定性差等不足。

5 实验分析

为验证本文改进后的算法效果，以文献[12]的案例见表4作为本文算法实验的测试数据，板材宽度为400。进行50次实验，各种算法种群内板材最优利用率的均值对比见图10。实验采用种群A见表5的遗传策略，分别结合最低水平线排样算法，最低水平线搜索排样算法，最低水平线择优插入算法，本文提出的最低水平线启发式搜索算法。

图10 种群A与各排样算法结合实验效果对比

表5 种群A相关参数

根据图10，对随机初始的种群A迭代的情况观测可以看出来，由于最低水平线启发式搜索排样算法可以更频繁地动态调整矩形件的排放顺序，种群内初始利用率比其他算法更高。同时，更频繁地动态调整矩形件的排放顺序也意味着更优秀的搜索能力，也弥补传统遗传算法局部搜索能力不足的缺陷。

在种群A20次迭代终止后的基础上，开始种群B迭代，种群B相关参数见表6。混合种群由随机和按面积大小排序的个体组成初始种群，迭代过程参考种群A的过程，其相关参数见表7。随机种群A，种群B，混合种群结合本文排样算法的对比实验见图11。图12是混合种群和随机种群A结合本文排样算法在迭代过程中种群内相似度对比。

表6 种群B相关参数

表7 混合种群相关参数

图11 各种群结合本文排样算法实验效果对比

根据图11，种群A内进行两点交叉，可以有效在离散解空间内搜索最优解，在后续的迭代中可以稳步提升种群内最优板材利用率。

图12 混合种群与随机种群A种群内相似度对比

图13 50次实验最优结果

表8 13组测试用例实验结果对比

混合种群由于加入部分按照面积大小排序的个体，初始适应度高比随机种群的更高。然而50代左右由于种群内多样性降低，陷入局部最优解，搜索停滞，出现过早熟问题。种群B在种群A的基础上迭代，可以有效利用信息，初始值比混合种群更好，同时种群B通过与种群A交叉的方式进行迭代，可以跳出局部最优解，直到100代左右算法收敛，避免了过早熟。

根据图12，混合种群60代左右种群内相似度到达较高的50%，对比采用相同的遗传过程随机种群的相似度在120代左右到达50%。说明混合种群在迭代的前期种群多样性迅速降低，导致算法过早熟，无法跳出局部最优解。

图13为实验中得到的最优结果，板材的利用率到达96.36%，图中黑色部分代表提高最低水平线时形成的没有利用的空洞。

为进一步测试本文算法的普适性，采用通用的测试用例，文献[18]中的13个实验测试用例进行实验并与文献[16]的IAGSA算法、Burke[18]的BF 算法、Huang[19]的HA算法做比较。种群A相关参数同表5，种群B相关参数同表6，对每个测试用例单独实验20次后统计结果见表8。

由表8可见，本文算法在此13组测试用例上表现优秀，说明算法实用性强，且稳定性很高，最优值与平均值差距很小或者没有差距。

6 结束语

本文通过启发式判断是否有更加合适的未排放矩形件来代替当前要排放的矩形件，动态调整矩形件排放顺序，改进了传统的最低水平线排样算法，可以有效提高板材利用率，减少板材空间的浪费。针对遗传算法收敛速度慢，过早熟问题，本文采用双种群遗传算法，结合先排放大矩形件，后排放小矩形件规律，改进了交叉算子，有效提升遗传算法的稳定性和在离散解空间的搜索效率。实验结果表明，本文改进后的算法具有较好的实用性。在未来的工作中，将从满足工业界中特殊的工艺要求的角度出发，继续探讨排样问题。