基于禁区惩罚函数和MPC倍增预测的车辆避障研究

花晓峰，段建民，田晓生

北京工业大学 城市交通学院，北京 100124

1 引言

对于无人驾驶智能车辆的安全行车而言，障碍躲避是车辆行驶控制的核心任务。由于智能车辆只能在道路上行驶移动，而且路线也是严格受限的，遇到的只有车辆、行人等特定的规则障碍，因此移动式机器人避障的算法思维并不能完全应用于车辆避障。由于车辆系统结构复杂，存在高度的非线性时变特性，因此有效地进行系统建模，选取快速、可靠的控制策略是车辆控制的重要基础。

模型预测控制（Model Predictive Control，MPC）是针对被控对象的线性化模型求解未来时刻的有约束最优解，并通过反馈机制更新系统状态来达到对系统实时在线控制的目的。预测控制以预测模型为基础，理论上不受系统的时变与非时变、线性与非线性、有无时滞的影响，在复杂系统控制方面取得了很大成功[1-2]。在智能车避障控制应用方面，文献[3]提出了基于人类驾驶行为的预测避障方案，但在避障环节采用了预瞄点搜索、MPC控制、PID控制多重模块，导致避障系统过于复杂；文献[4-5]分别从受控自回归积分滑动平均模型和模拟退火算法求解目标函数方面阐述了轨迹跟踪控制方案，但均把重点放在了单纯的车辆轨迹规划层面，对于以障碍检测、障碍预测为基础的轨迹重规划方面内容较少涉及；文献[6]采用了预测触觉反馈（Predictive Haptic Feedback）的思路实现了障碍躲避，但方案只完成了换道，并没有进行避障换道之后的返回原车道实验；文献[7-10]通过模型预测与不同算法融合阐述了避障策略，但并未考虑车辆的长宽尺寸，亦无法判定车体是否能安全地避免与障碍发生碰撞。真实的行车环境中，障碍物和车体的尺寸都不可忽略，因此即便将车体抽象为质点，也必须要考虑其与障碍拉开足够距离的问题。因此障碍相对于车辆质心而言必然会存在一个“禁区范围”。

针对以上问题，本文以模型预测控制算法和车辆动力学模型为基础，以前轮转向车辆为实验对象，对障碍物边界点的确定引入以阶跃函数为基础的禁区边界惩罚函数，禁区边界长度以车辆尺寸为依据，以保证车身不与障碍边界点触碰；在避障路径重规划环节引入预测距离倍增的方案，以弥补因预测距离过短导致无法在远距离处检测到障碍物造成避障失败的缺陷。

2 预测模型

2.1 车辆动力学建模

车辆运动过程中存在多个状态变量，因此需要建立复杂的动力学微分方程组。假设车辆是只可作横向、纵向、横摆运动的三自由度前轮驱动车辆，则可等效为二轮自行车单轨模型。分别建立相对地面的世界坐标系OXYZ和相对车辆自身的车体坐标系oxyz，如图1，两坐标系以坐标轴字母大小写进行区分。车体系原点位于车辆质心，x轴方向为车体纵向，y轴沿车体横向与x轴垂直，z轴方向由右手系法则确定，横摆角φ是车体系x轴与世界坐标系X轴的夹角，其逆时针方向为正方向。

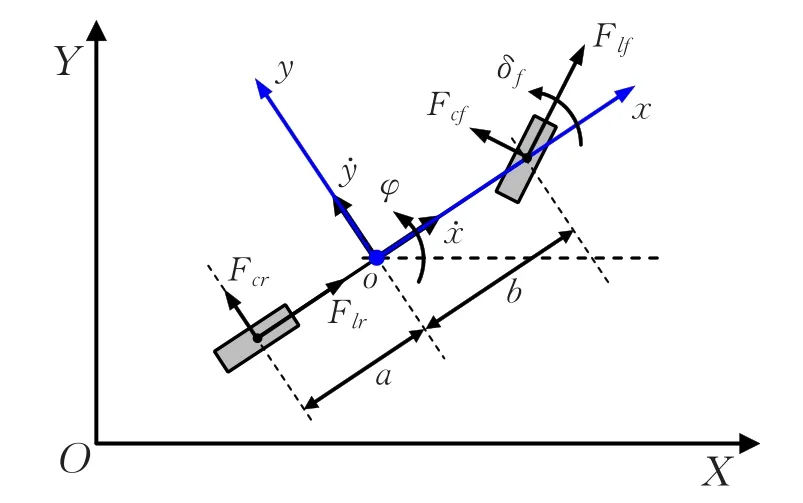
图1 二轮单轨前轮驱动式车辆动力学模型

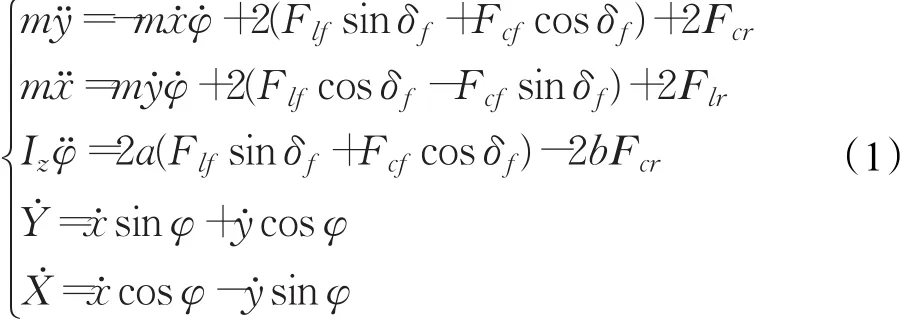
根据运动学坐标转换和牛顿第二定律可得受力平衡方程：Flf、Fcf分别为施加给前轮的纵、横向力，Flr、Fcr分别为施加给后轮的纵、横向力。前轮驱动车辆的后轮不能转向，故后轮偏角恒为0，即δr≡0。前轮的合速度即为车辆的输入速度，即 vin=x˙2+y˙2，恒定速度时 vin为常数。在侧偏角较小时，动力学模型可进行线性近似化，由无穷小定理和轮胎线性模型，可将式（1）转化为前轮小偏角和线性化轮胎模型下的车辆动力学非线性模型[11-12]：

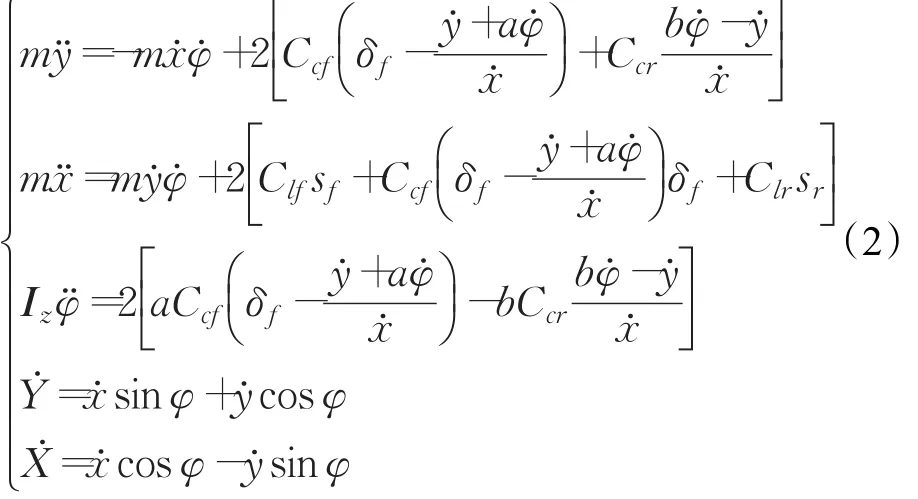
m为车体质量；Ccf、Ccr为前、后轮侧偏刚度；Clf、Clr为前、后轮纵向刚度；a、b为质心的前、后车轴距离；sf、sr为前、后轮纵向滑移率；Iz为车体关于z轴的转动惯量。角度单位全部为弧度。选取状态量ξ为(˙˙φ φ˙YX)T，控制量 u 为 δf，输出量 η=Cξ=(φ Y)T，式（2）可以写为由ξ、u、η组成的非线性函数状态空间式：

2.2 车辆预测模型

2.2.1 状态方程

考虑无人驾驶车辆对控制器的实时性要求，首先需要对模型进行线性化。采用近似线性化思想，将式（3）写为标准线性模型式：

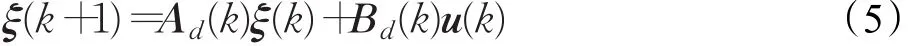
其中Ad(k)=I+TA，Bd(k)=TB。

式（5）出现了ξ(k+1)，它表示的是以当前k时刻为基准未来下一时刻的状态。模型预测的思想便以此为基础，通过递推法逐步推导出预测时域内未来某一时刻的状态。

2.2.2 目标函数

目标函数需要保证车辆快速平稳跟踪规划的期望轨迹，优化对象为系统状态量和控制量。采用偏差式目标函数以消除静态误差，即[13]：

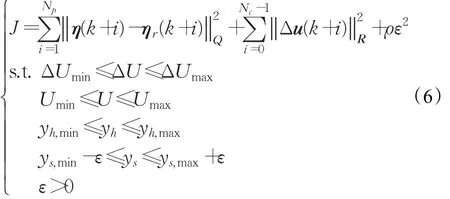
定义状态偏差量：

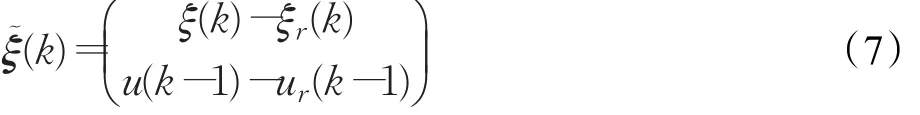
可得：

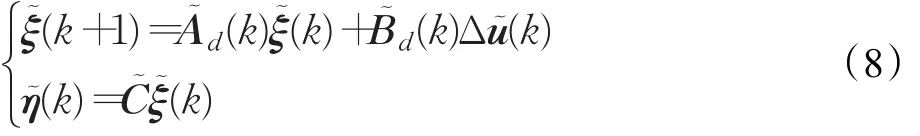
得最终的广义预测输出表达式：

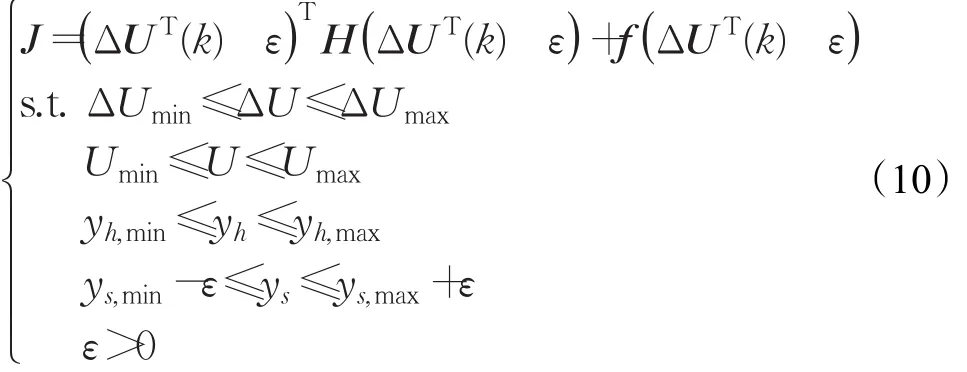
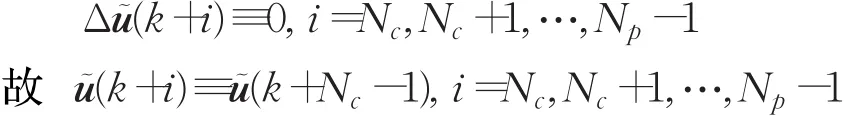
2.2.3 反馈环节

每一控制周期内对式（10）求解完成后得到控制时域内的一个控制输入序列ΔU*：

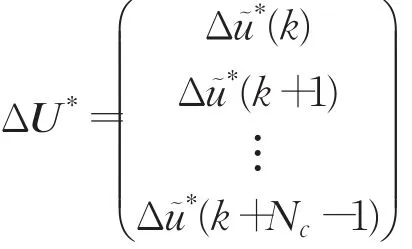
根据反馈原理将第一元素作为控制输入增量作用于系统，即：

进入下一控制周期后重复上述优化过程，再次求得下一控制周期的最优控制输入增量。

3 避障规划

3.1 惩罚函数

障碍物点阵信息通常由雷达通过扫描障碍物得出，惩罚函数可以单独针对障碍物点进行设计。惩罚函数是通过与障碍物点之间的距离函数来调节避障优化函数值。惩罚函数可采用关于距离的反比例函数实现，如式（12）[12]：

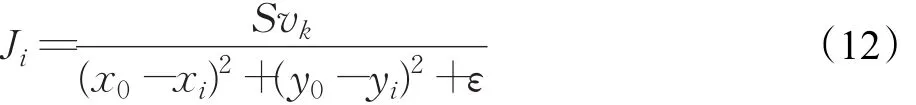
k为预测时域内的某一时刻，(x0,y0)是该时刻车辆质心的坐标，(xi,yi)是第i个障碍物点的坐标（均在世界坐标系下），ε＞0是一个防止分母为0的保护常数，vk是当前时刻的合速度，S是权重系数。

该方法的缺陷首先是对于障碍边界的划分较为模糊，其次是并且未能考虑车身尺寸。在避障预测时会出现无法正确确定障碍边界、甚至规划路径穿过障碍物的错误结果；即使规划路径能够避开障碍物，也有可能因路径过于靠近障碍物而导致车身与之发生碰撞。因此本文提出一种基于阶跃函数的禁区边界式惩罚函数策略，即：

式中M是一个充分大的正数，R*是临界（禁区）半径。车辆质心位于车体几何中心。令R*等于车身外接圆半径，相应地，每一个障碍物点都可以认为存在一个以自身为圆心，半径为R*的禁区圆。预测时域内某一时刻得出的车辆质心坐标如果进入了障碍物点禁区圆内，由于M的存在，会导致规划目标函数值急剧增大，迫使预测控制器重新搜索最优控制量，如图2。

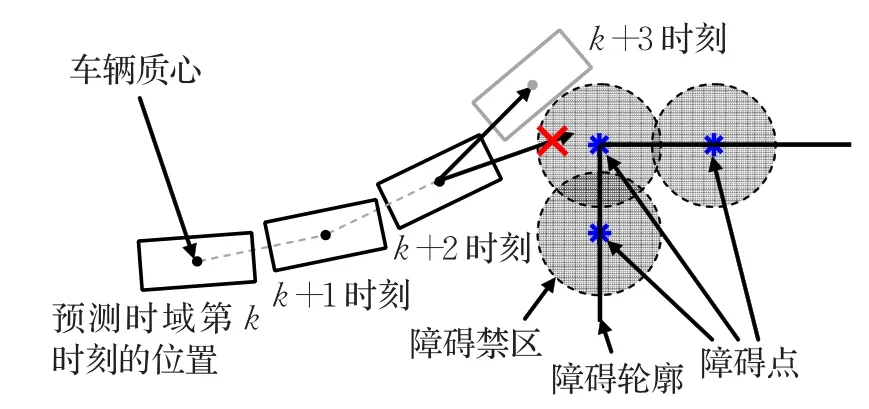
图2 障碍点与预测时域内不同时刻的车辆位置的关系

由于轨迹重规划环节计算量较大，为了简化计算，规划层采用运动学模型，可以更好地兼顾控制性能和计算速度[14]。在规划层中，设状态变量ξ 为(y ˙ x˙φ YX)T，离散化后有：

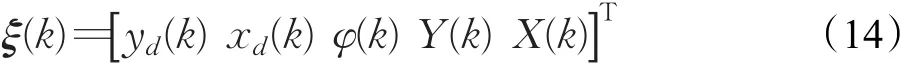
某一预测时刻k下得到的k+1时刻状态变量为：

由于车辆输入速度为恒定，因此在任意的k时刻，vin,d(k)为常数，前轮偏角δf即为控制量。由于控制时域过长会导致MPC控制不稳定，因此控制时域Nc应尽可能短，这里取Nc=1，则令U=()δf，η(k)=[]Y(k)，局部参考路径ηr(k)=[ ]Yr(k)，可得轨迹重规划的目标函数：N为障碍物点的个数。式中的η、U、Q、R与第2章中的不同，它们是属于规划层环节，并不用于车辆的运动控制策略。式中：

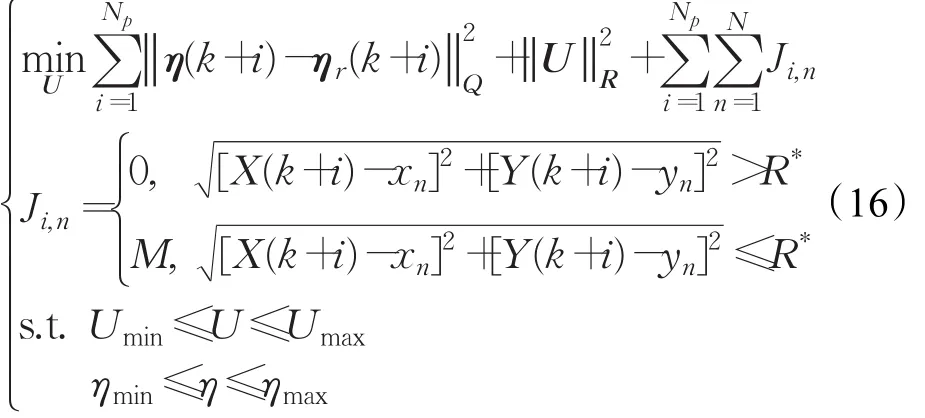
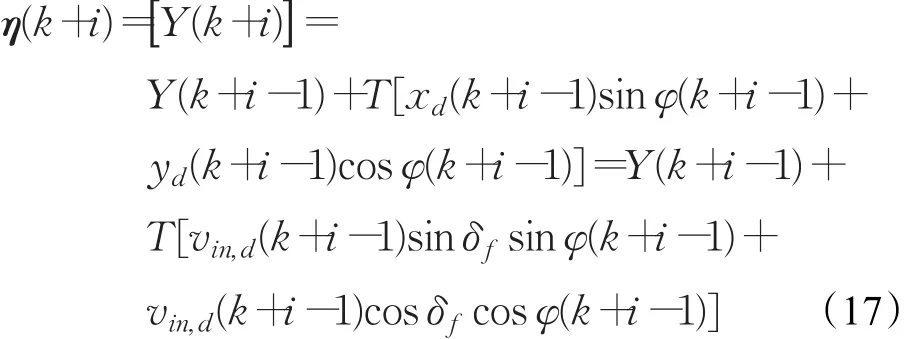
因此可知输出量η是关于控制量U=(δf)的函数。由于控制时域仅为1，因此当时刻i≥1时，控制量的变化量恒为0，即 ΔU(k+i)≡0,i=1,2,…,Np-1，因此预测时域内有U(k+i)≡U(k)≡(δf)。优化完成后得到车辆在当前位置点的最优前轮偏角量，按照MPC反馈的定义，直接代入式（15），更新状态量即可得到新时刻的车辆各个状态值。

3.2 障碍检测

传统的障碍检测是将障碍物视作点障碍，并以该点构造基于距离的反比例函数作为惩罚函数。规划层采样时间短，且预测时域一般不能过长。仿真实验观测表明，车辆在某一时刻实际预测距离很短，对于点障碍物不考虑尺寸则可以完成路径的避障规划。而对于长宽不可忽略的大障碍物，其尺寸明显大于所预测距离，使用同样的方法会导致车辆较远时根本无法探测到障碍物。本文采用另一种策略，在规划层进行优化期间，对采样周期进行倍数扩增，例如3倍或5倍，然后再将优化得到的结果直接用于状态更新，状态更新过程中不使用周期倍增，这样便可使车辆在较远位置即能探测到障碍物，如图3。

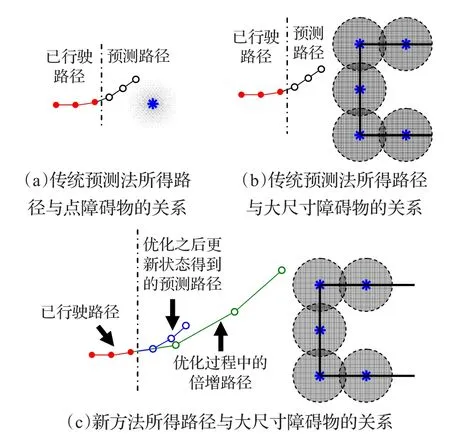
图3 预测路径与障碍物的关系

设扩增倍数为W，则式（17）中η改写为：

同理障碍惩罚函数中的X(k+i)和Y(k+i)分别为X(k+i)+TW[xd(k+i)cosφ(k+i)-yd(k+i)sinφ(k+i)]和 Y(k+i)+TW[xd(k+i)sinφ(k+i)+yd(k+i)cosφ(k+i)]。

这样优化过程中的预测位移X和Y相应地被扩大，完成后得到最优前轮偏角量记为δ~*f，代入式（15）更新状态，在更新状态时未使用扩增倍数为W。通过这种手段便能使车辆在距离障碍物较远位置即可提前预知障碍物的存在从而及时调整当前状态，为后续能够得到正确的规划结果奠定基础。

3.3 轨迹拟合

轨迹重规划得到的是一系列散点，由于控制层输入端口数量有限，显然不能将离散点直接输入控制层。曲线拟合是一种主要的替代处理方式，由于车辆的运动学和动力学存在一阶、二阶特性以及连续特性，因此采用三次多项式作为拟合曲线，其表达式为[12]：

纵向位移与横摆角拟合多项式的各项参数向量(a b c d)和(w x y z)将作为轨迹重规划的输出值。

4 实验方案设计

4.1 实验平台

选用CarSim车辆动力学作为仿真平台，利用Matlab/Simulink搭建控制系统并通过S函数编写控制策略，系统框图如图4。

CarSim输入4个变量，依次为左、右前轮偏角和左、右后轮偏角；输出6个变量依次为车体系横向速度、车体系纵向速度、横摆角、横摆角速度、世界坐标系下的纵向位移、世界坐标系下的横向位移，路面摩擦系数设定为0.85。

4.2 实验参数与工况设定

实验中采用双移线轨迹作为跟踪期望路径[15]。模型预测控制需要添加相应约束，控制量只有前轮偏角δf，设车辆方向盘在打死状态时前轮偏角最大值为30°，前轮偏角变化量Δδf最大值设置为每采样周期0.85°。因此控制量及控制量增量约束分别为：

（1）单一障碍物 I：障碍物中点坐标（32.5，0）；车辆速度为5 m/s（18 km/h）；Np,pl=19，Nc,pl=1，Tpl=0.05 s；Np,ctrl=19，Nc,ctrl=1，Tctrl=0.03 s；

（2）单一障碍物Ⅱ：障碍物中点坐标(32.5,2)；车辆速度为 16.67 m/s（60 km/h）；Np,pl=19，Nc,pl=1，Tpl=0.02 s；Np,ctrl=22，Nc,ctrl=1，Tctrl=0.095 s；

（3）双障碍物：障碍物1中点坐标(32.5,0)，障碍物2中点坐标 (72.5,1)；车辆速度为 10 m/s（36 km/h），Np,pl=19，Nc,pl=1，Tpl=0.02 s；Np,ctrl=25，Nc,ctrl=1，Tctrl=0.03 s。

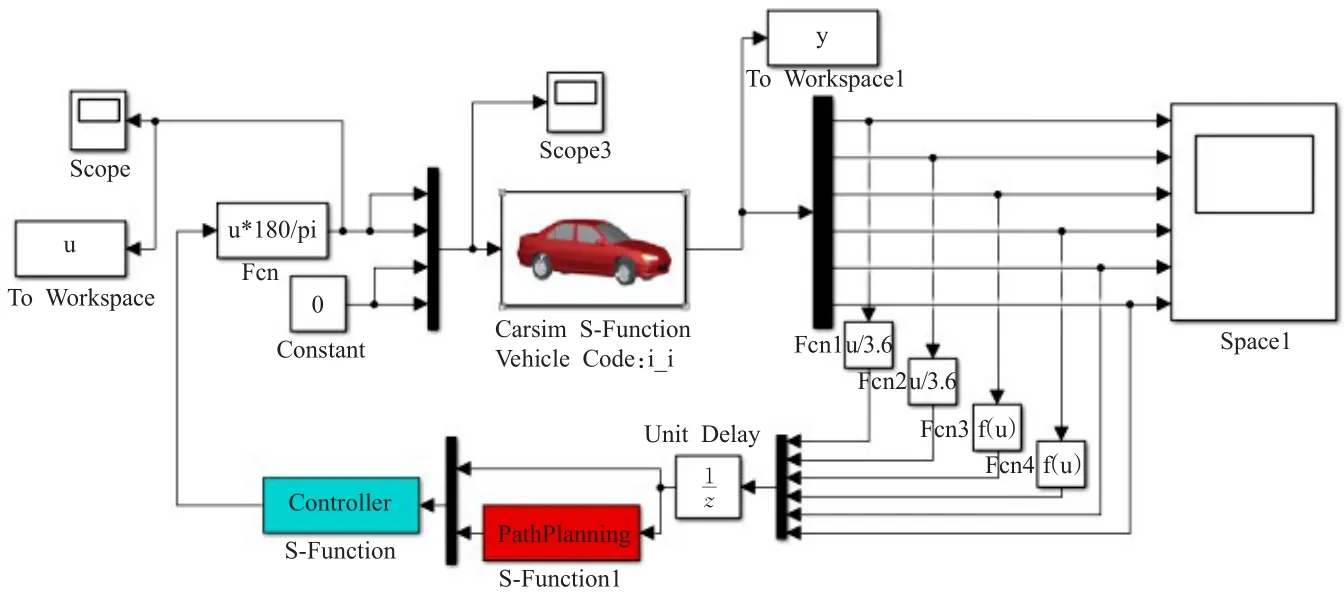
图4 系统框图

5 结果与分析

5.1 实验图像

黑色曲线为参考轨迹。实验每隔一定时间以矩形框显示某一位置处的车体轮廓；蓝色星号轨迹为传统方法即使用反比例惩罚函数及不加预测倍增方法得到的实验结果；红点轨迹为使用本文方法得到的结果。在纵坐标位移图中，本文方法得到的每一处实际位置点上均以一系列绿色须状线条显示不同种规划方案。横摆角曲线中的黑色曲线表示参考轨迹上对应横坐标处的车体期望横摆角。前轮偏角及变化量曲线使用蓝色虚线划定其约束的上下限。

工况1（单一障碍物 I），如图5～8。

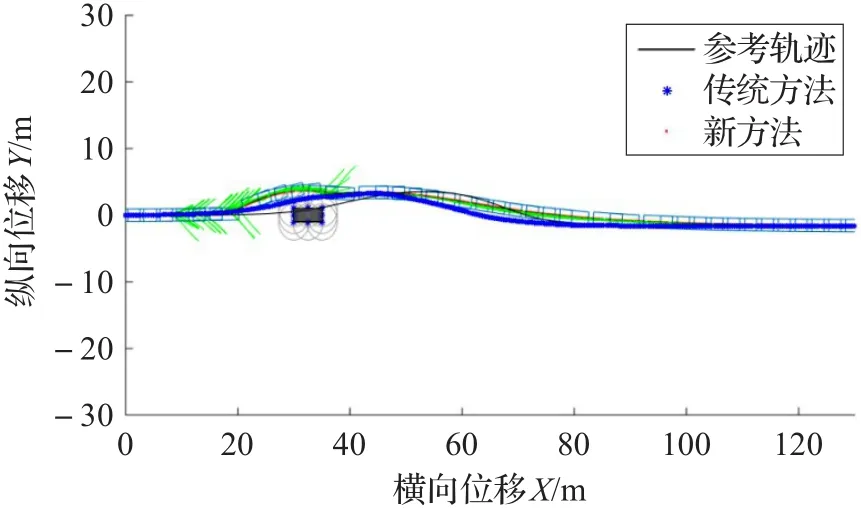
图5 车辆行驶轨迹曲线

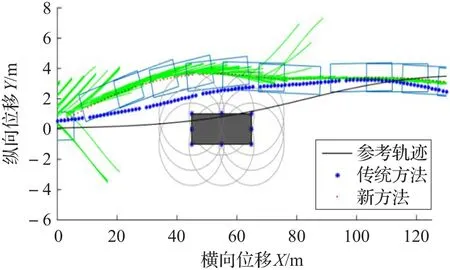
图6 障碍物附近的局部放大图

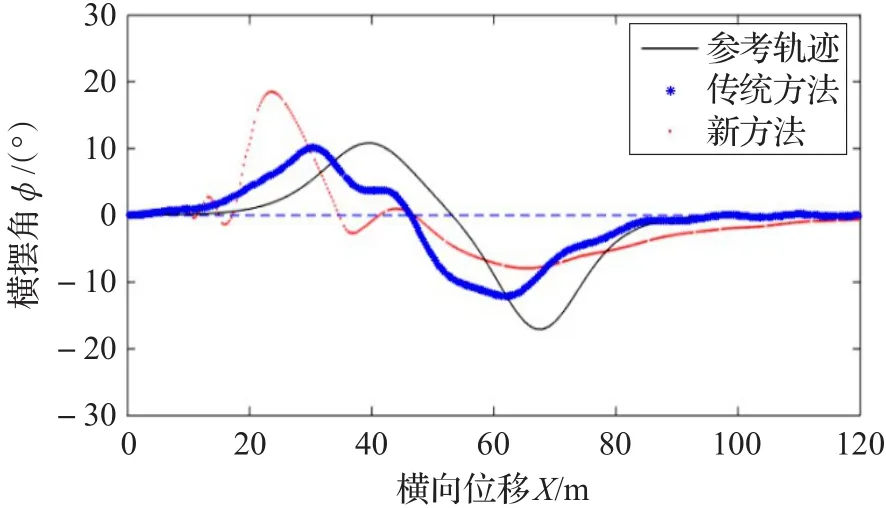
图7 车辆横摆角曲线

工况2（单一障碍物Ⅱ），如图9～12。

工况3（双障碍物），如图13～16。

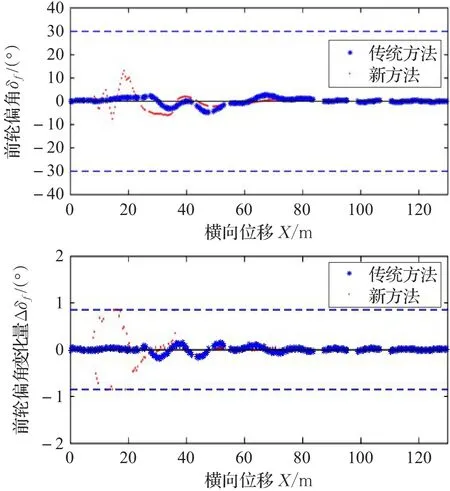
图8 前轮偏角及变化量曲线

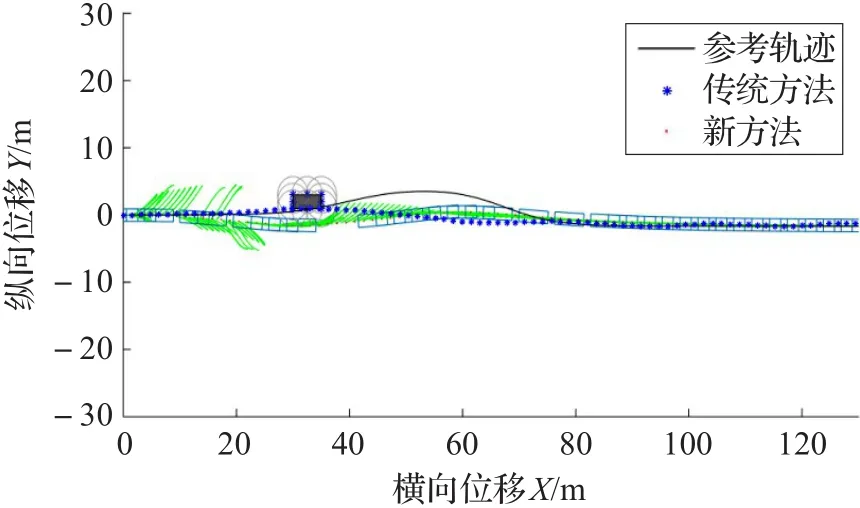
图9 车辆行驶轨迹曲线

图10 障碍物附近的局部放大图

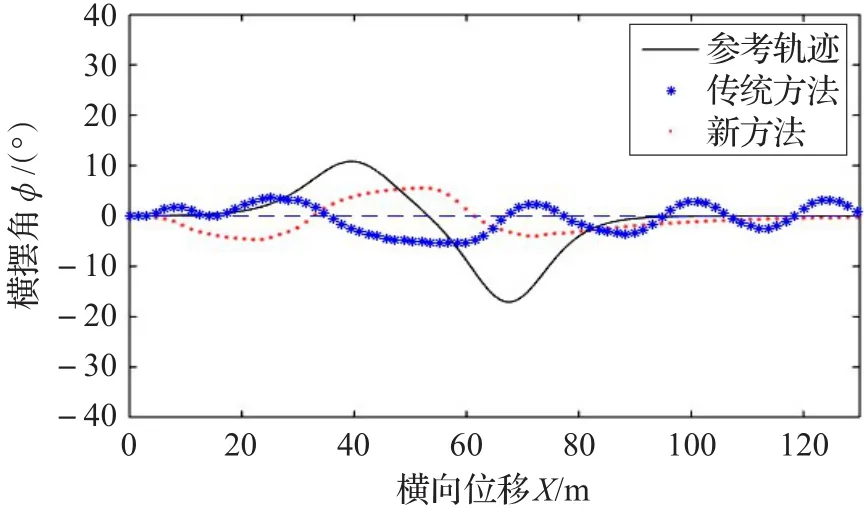
图11 车辆横摆角曲线

5.2 结果分析

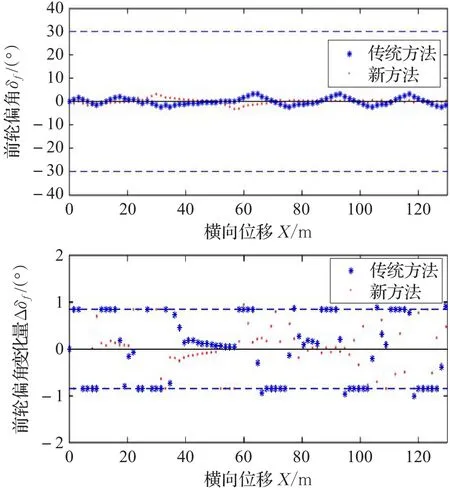
图12 前轮偏角及变化量曲线

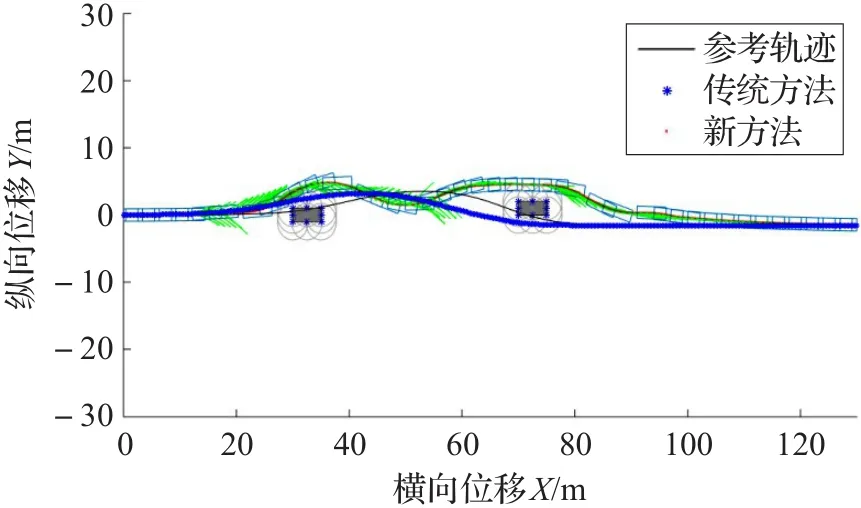
图13 车辆行驶轨迹曲线

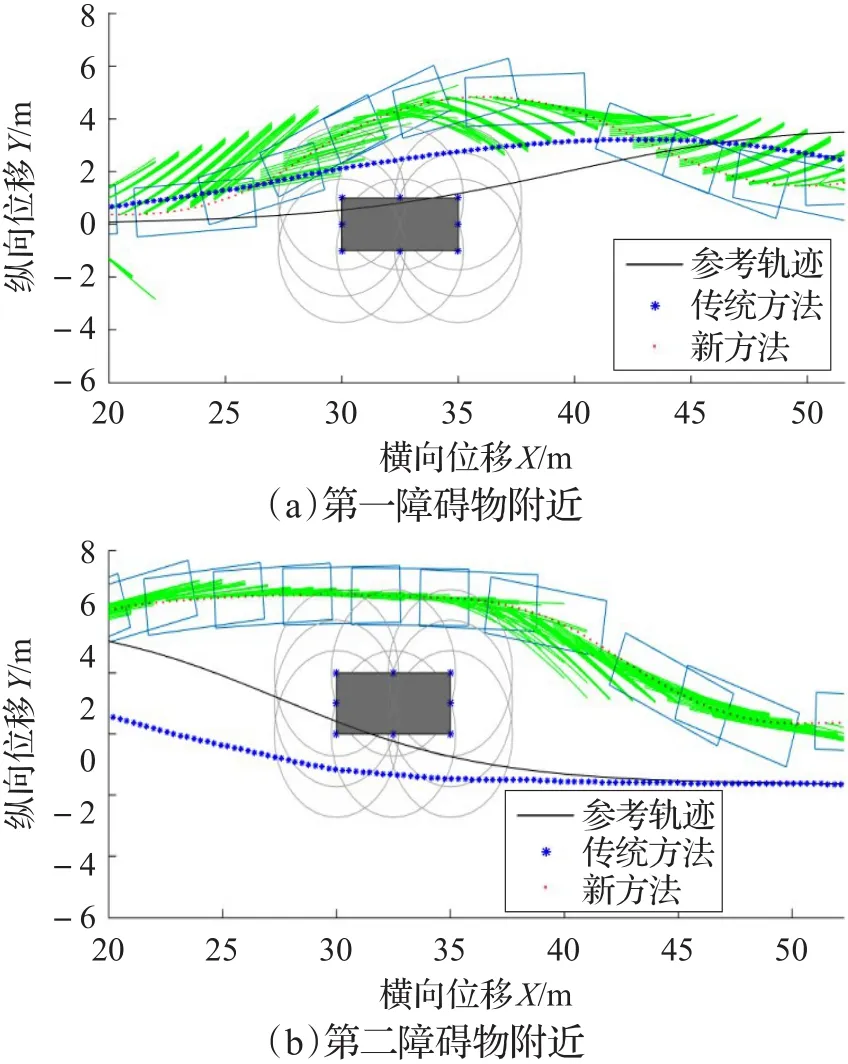
图14 障碍物附近的局部放大图

图15 车辆横摆角曲线

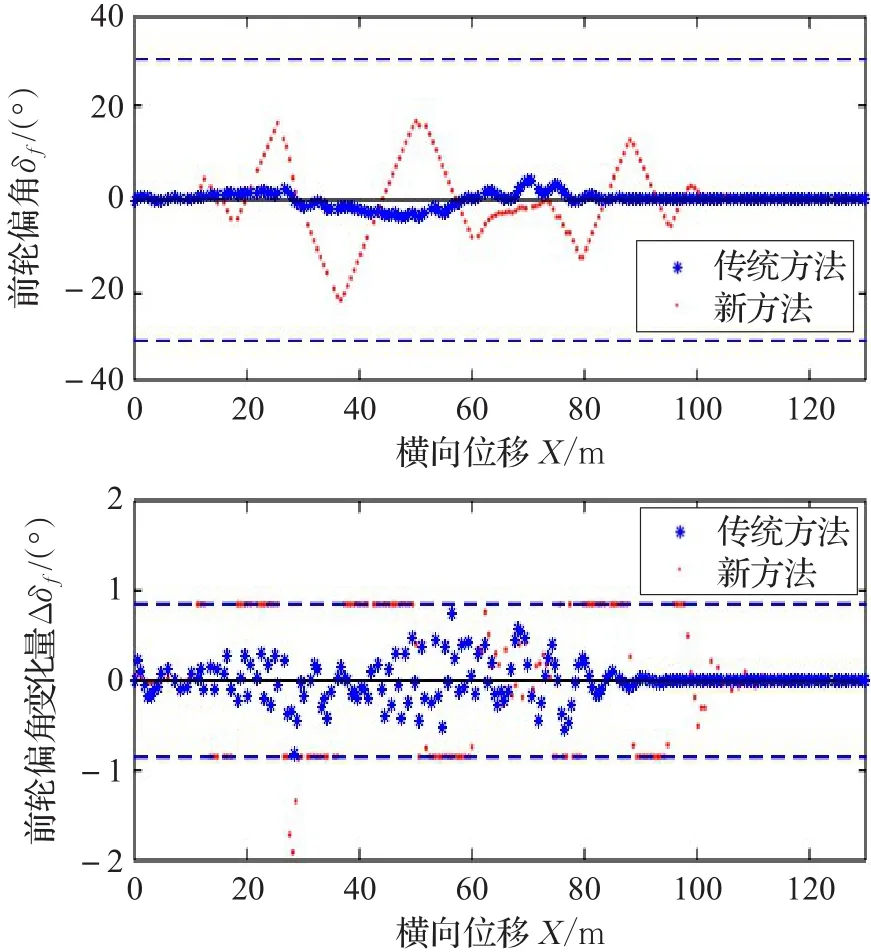
图16 前轮偏角及变化量曲线

三种工况下分别绘制出车辆轨迹、横摆角及前轮偏角曲线。与传统方法进行对比，可以发现通过本文方法车辆能够完成避障，车辆横摆角和前轮偏角均收敛于0°，且前轮偏角及前轮偏角变化量的值均在约束范围内。对于传统方法，图5和图13可以看到工况1和3下车辆质心能避开障碍；图7和图15的车辆横摆角都能收敛于0°；图8和图16的前轮偏角亦收敛于0°且在约束范围内；但是障碍邻近放大图（图6和图14）可见车辆质心过于深入障碍物点禁区范围，这样将导致车身擦碰障碍物；图9和图10可以看到工况2传统方法下车辆质心触碰障碍物，避障失败，而且从横摆角图（图11）、前轮偏角图（图12）可以发现横摆角和前轮偏角都无法收敛，使得车身围绕参考轨迹不断摇摆。另外，在各个仿真工况下的障碍物附近区域局部放大图中可以发现，新方法车辆质心轨迹由于预测规划误差的缘故略微擦过了障碍物的最外层禁区边沿，但是通过车辆轮廓线可以发现车身已经远离障碍区，说明避障成功，因此轨迹的微小越界是可以接受的。

6 结束语

本文提出了划定障碍物点禁区边界的方案，使用分段函数法进行障碍物点的禁区边界划定，解决了关于距离的反比例惩罚函数对于障碍边界划定不清的问题；在规划层中进行轨迹重规划时，采用了预测周期倍增法，将倍增后得到的预测位置点应用于未施加倍增的运动学方程中进行状态更新，从而使得车辆在较远位置即可提前预知大尺寸障碍物，及时做出转向调整；对不同工况进行仿真测试，并与传统方法进行比对，结果满足预期要求，验证了算法的可行性。