区块链中的自私挖掘研究与分析

高永琳，程晓荣

华北电力大学 控制与计算机工程学院，河北 保定 071003

1 引言

区块链技术因其去中心、安全、可追溯、去信任等优势被研究、重视[1-3]。在能源互联网、金融支付、物联网等领域正处于研发探索阶段[4-7]，应用前景广阔。“分叉”是区块链系统中的普遍现象，浪费挖掘算力，影响区块链系统的运作。自私挖掘就是利用分叉现象“非法”获得区块收益的攻击策略。因此，对区块链的安全性进行研究十分重要。

由于区块链是一项新兴技术，目前国内外学者对区块链攻击方面的研究还不够完善，提出了一些降低攻击效果的方法[8-10]。针对区块链的攻击大体上可分为双花攻击、自私挖掘、女巫攻击、日蚀攻击等。根据已有的研究文献，自私挖掘攻击是一种选择性地公布区块的挖掘策略，是由部分挖矿节点组成的一个矿池。国外学者主要从挖掘策略和预防策略等方面对自私挖掘进行研究与分析。一个自私的矿工可以通过隐藏区块来增加其相对的挖矿收入。研究表明，在区块没有被确认的情况下进行的交易是不安全的，确认的数量越多，交易越安全[11]。康奈尔大学的Eyal和Sirer首先提出了自私挖掘的概念并对其研究，在采用自私挖掘攻击时，一个起初只拥有33%挖矿算力的矿池能逐渐获得超过50%的挖矿算力[12]。在研究早期，自私挖掘被视为一种块丢弃攻击（block discarding attack）而进行研究[13]。文献[14]探讨了传播延迟因素在自私挖掘攻击中对区块链攻击效果的影响。针对自私采矿，文献[15]提出一种使用不可伪造的时间戳来防御自私挖掘的措施。文献[16]采用一种颠覆性的采矿策略，设计出一种具体的、实际的抵御攻击的区块。为了保障系统安全，文献[17]研究了自私挖掘的算力阈值，提出限制自私挖掘算力的策略，与本文的研究有相似之处。文献[18]提出一种向后兼容的防御区块隐藏的机制，一个没有被公布的区块会被忽略掉。

通过文献综述可知，国内外对于自私挖掘在区块链方面的攻击研究已经具有一定的理论基础，研究的分析侧重点也不同。然而自私挖掘对区块链的攻击方面的研究尚未引起足够重视，国内缺乏对自私挖掘过程的模型的研究。为研究算力对自私挖掘收益的影响，本文设计了一种挖掘策略，通过求解自私与诚实挖掘概率大小的方法来决定是否公布隐藏的区块，从而提高自私挖掘收益的相对份额。文章分析了区块链平台下的自私挖掘过程，计算出了自私挖掘的算力阈值。

2 自私挖掘

2.1 自私挖掘原理

自私挖掘池选择性地释放挖到的区块，有时放弃自己当前的收入，但常常突然释放更多的块，迫使其他网络丢掉自己的块或者失去应有的收入。短期内自私挖掘的收入会较低，同时这也降低了其他块的收入。而保持中立的节点就可能加入自私挖掘池的队伍来增加他们的收入。最终，自私挖掘池的队伍会逐渐扩大到超过50%的大小，网络的控制权由自私挖掘池掌握。

2.2 过程分析

区块收益由目标动作所控制，其最优决策就是在什么情形下选择公布区块以获得最优收益。本文使用SAPV模型描述自私挖掘的过程，即以下多元组：

S,A,P,V

S是有限状态集，S={(t,g)}，(i,g)指当前i步骤处于 g 状态，g=（State1，State2，State3，State4，State5，State6，State7）。

A是行动集，A()S是在状态S下可采取的行动集，a∈A()

S={h（隐藏），p（公布），a（接受）}。

P是状态S×S×A→[ ]0,1是在可用行动a下状态转移S→S'的概率函数，表示动作a下，当前状态下挖到下一个区块的概率。

V表示当前状态下的期望收益。

下面对相关参数进行定义：

集合 L=（0'，0，1，2，3），表示自私挖掘链相对于诚实链的领先数量，0表示只有一条公共链，0'则表示含有两条长度为1的链。

La表示目前自私挖掘链上的长度，Lh表示目前诚实链上的长度，令△L=La-Lh，表示自私挖掘链相对于公共链的领先数量。

αa∈[ 0,1 ]表示自私矿池的算力，1-αa则表示诚实节点的算力。

β表示选择在矿池中挖掘的诚实节点的数量。

Ca表示自私挖掘链，Ch表示诚实链。

Na表示自私挖掘池目前挖掘到一个新块，Nh表示诚实链挖掘到一个新块。

区块链系统收益来源于两部分，一部分来源于诚实节点，该部分节点遵循正常的挖掘协议，一旦诚实节点挖掘到一个新的区块就会立刻向全网公布，由此获得区块奖励；另一部分收益来源于自私挖掘池，自私挖掘池会选择性地公布挖到的区块。分析区块链系统的挖掘过程，当出现分叉情况时，为防止无限状态，限制链的最大深度为6个区块。状态如图1所示，共有7个基本的分叉状态图。

图1 自私挖掘基本状态

挖掘过程中，当自私挖掘链的深度与诚实链的深度都为1时，为获取更多的利益，此时诚实节点中的一部分节点可能会加入到自私挖掘池中，如图1中的State2。每种状态下，此时若是自私挖掘池发现一个区块，自私挖掘池都能依一定概率做出不同反应，公布、隐藏、接受是自私挖掘池将采取的动作；若是诚实节点发现新的区块，则只会选择公布新区快。自私挖掘池采取不同的动作，结果也不同，结果如表1所示。

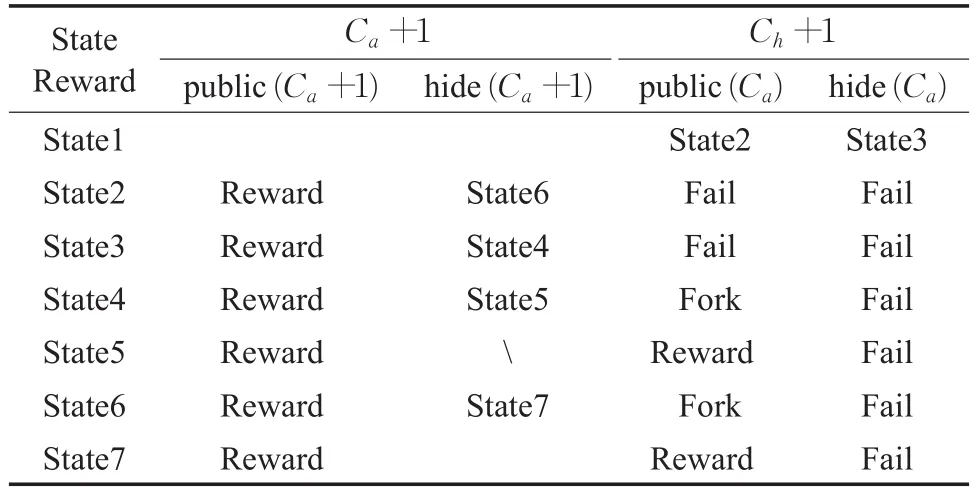
表1 自私挖掘状态转换

说明：“”表示自私链达到公布条件，此时必须公布；Fork表示出现两条长度为2的分叉链；Fail表示诚实节点首先挖到新区快，且链的长度超过自私挖掘链，此时自私链上的区块自动失效，自私挖掘失败；Reward表示自私链上有区块收益。

2.3 概率分布计算

2.3.1 诚实挖掘概率分布

区块被挖到的概率与算力的关系很大。由文献[19]知，正常的挖掘过程近似于泊松分布，在恒定的算力下，区块以一定的概率被独立开采。正常情况下，每10 min系统中就会有一个区块被挖掘出来，系统会根据区块被开采出来的的速率自动调整难度以保持速率在10 min左右。由文献[15]可知，一个诚实节点挖到下一个区块的概率为：

其中，αi表示节点的算力，d表示难度值。单位时间内节点挖到区块的数量为；假设挖到每个区块获得奖励货币为r，则单位时间获得的奖励为。将所有诚实节点看做一个整体，则αh=1-αa=∑αi为诚实部分的节点算力。

2.3.2 自私挖掘概率分布

自私挖掘在矿池节点不变的情况下算力基本不会变化，所以单位时间内发现一个区块的概率基本恒定为pa=1-e-1α0at。假设自私节点xi对区块进行挖掘，当挖到一个区块时记xi=1，否则xi=0；由中心极限定理可知，自私矿池节点X=x1+x2+…+xn之和的标准化变量服从如下分布：

式中μ为期望值，σ为标准差。

而自私挖掘在挖矿过程中会出现诚实节点加入的情况，这会增加矿池的算力，所以概率分布会发生变化。式（3）P′表示挖掘矿池算力变化时新区块被发现的概率分布。

公式（3）中，当 P′=(1 -β)(1 -pa)，表示在状态2的情况下有一部分节点加入到了矿池中，而新区块被诚实节点发现；概率β(1 -pa)表示在状态2的情况下，被诚实节点发现的新区块被链接在自私挖掘链上。

2.3.3 追赶概率

由文献[19]，假设诚实链能够弥补z个区块差距的概率为qz，则：

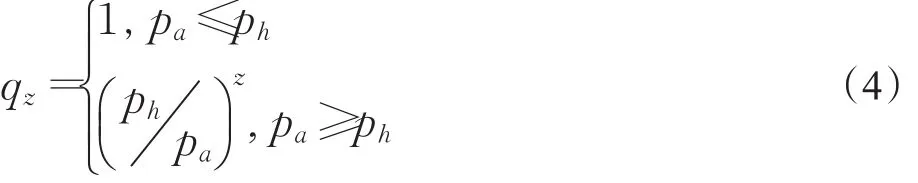
由公式（1）知用已挖掘出k个区块数量的诚实挖掘概率密度乘以依然能追赶上的概率为：

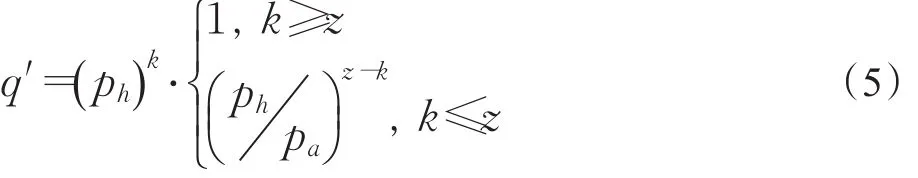
2.4 算法求解

对于自私挖掘而言，关键的问题是选择在什么情况下公布隐藏的区块[20]，以保障收益。为保证自私挖掘能成功，采用以下挖掘策略：

（1）在ΔL=0且已出现分叉时，当下一个被发现的区块为Na时，立刻公布区块并链接在自私链上。

（2）在ΔL=1时，当下一个被发现的区块为Nh时，立刻公布自私链上的区块；而当被发现的区块为Na时，将Na链接在自私链上并隐藏区块，继续挖掘。

（3）在ΔL=2并且分叉的情况下，当下一个被发现的区块为Nh时，此时计算在已挖到一个区块数的前提下挖到下一个区块的概率q'，并计算自私链在当前情况下挖到下一个区块的概率 pa，当q'＞pa，则自私挖掘链立刻公布所有隐藏的区块，否则只公布与诚实链相对应的区块；而当被发现的区块为Na时，将Na链接在自私链上并隐藏区块，继续挖掘。

（4）当ΔL≥3时，当下一个被发现的区块为Nh时，此时自私挖掘链公布的区块数应与诚实挖掘的区块数相同；而当被发现的区块为Na时，将Na链接在自私链上并隐藏区块，继续挖掘。

根据文献[10]，以自私挖掘的相对收益作为目标函数。系统总的收益基本恒定，所以以自私挖掘的相对收益份额作为研究的对象更具对比性。目标函数表示如下：约束条件为ΔL≥0。其中，ra()π表示自私挖掘池在策略π下的收益，rh()π则表示诚实节点的收益。由函数（2）知自私挖掘的收益ra与相对收益rrel成正比例关系。

3 仿真与分析

为验证本文所提模型的有效性，实验布置在总内存为64 GB的Linux服务器模拟进行，Go语言环境，采用计算机端口作为模拟的节点，节点之间通过消息进行通信，采用MATLAB工具编码仿真图像。

3.1 实验设计

事实上，挖矿收益受多种因素影响，包含区块大小、消息传播速率、节点之间的距离、挖矿计算难度等，由于实验主要分析矿池和诚实节点的收益情况，所以消息传播时的延迟时间、区块大小等因素在实验中被忽略。区块体的参数主要有区块大小（Blocksize）、前一区快的散列值（parentHash）、当前区块的散列值（Hash）、时间戳（timeStamp）、随机数（Nonce）等，将区块体的参数设置为默认值。

本模型所涉及的参数主要有自私挖掘算力αa、自私挖掘链上的诚实者比重β等。在共识算法方面，采用工作量证明机制（PoW），运用TCP/IP协议控制节点的信息传输。实验共设置1 000个模拟节点。实验目的一是测试自私挖掘矿池在不同算力下的收益效果，包括在不同β下时的收益变化情况；二是不同β下自私挖掘的阈值变化。

实验过程如下：

（1）首先在Linux服务器上模拟构建区块链节点，每个端口号代表一个节点，采用IP地址与端口号相结合的方式作为节点的标识。

（2）本实验将1 000个模拟节点分为两部分，一少部分为诚实节点，另一部分为自私节点。诚实节点遵循正常的比特币挖掘协议，矿池中的自私节点依照提出的SAPV模型进行挖掘，以与诚实节点的挖掘收益形成对比。

（3）针对公式（3），分别取 β 值为0、0.2、0.3、0.5、0.7、0.8、1，计算不同β下的概率分布；由于矿池算力αa小于系统算力的一半被认为是保障区块安全的前提，所以实验中，自私挖掘的算力值最大为0.5，分别取值0.1、0.2、0.3、0.4、0.5。当出现状态2的情形，修改诚实节点与自私节点的比例，将P′值带入SAPV模型中。

（4）根据公式（6），不断采集诚实节点与自私节点的收益数据，重复实验，对比在不同β下各部分的收益情况。

（5）在以上工作的基础上，分析各部分的挖矿收益，利用MATLAB工具编码计算β∈[ ]0,1条件下的算力安全阈值，即自私挖掘以某一最小的算力获得的收益高于诚实挖掘的收益。

3.2 实验结果及分析

自私挖掘矿池的算力影响矿池的收益，下面主要对比分析在不同算力下的矿池收益。对不同β下的矿池算力进行仿真实验。表2为系统中的矿池与诚实节点收益，由表2可知，当β=1时自私挖掘收益高于诚实节点收益；随着算力的增加，矿池收益持续增高，最大值在0.8附近，远高于诚实挖掘的最高收益值。验证了采用本模型时可以提高矿池的收益。

根据表2的实验数据进行图表绘制，图2为自私挖掘及诚实节点的相对收益。自私挖掘池的收入不断增加，这会吸引诚实节点陆续加入到其中，然而这不利于区块链挖掘协议的稳定运行。在自私挖掘链深度与诚实链深度相等的情况下，部分诚实节点会加入到矿池中。由图2知，随着矿池规模的增大收益值逐渐提高。当α很小时，诚实链与自私挖掘链的收益值差别不大；不同的是，随着α增加，自私挖掘收益值快速增长，诚实链上的收益值增长的速率则较缓慢，这是因为自私挖掘池中不断有诚实节点加入，提高了挖掘矿池的算力。

表2 节点收益

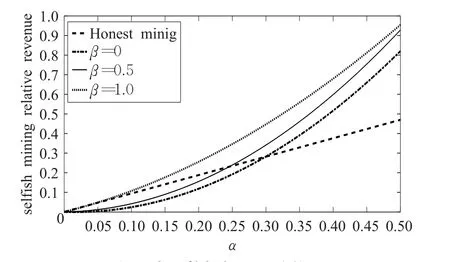
图2 自私挖掘相对收益趋势

图3 为不同β下的算力阈值，由图3知，阈值随β的增加而下降，即使当β值为0时，自私挖掘的算力也不可超过0.3，否则诚实链处于劣势中，这也印证了图2中当β=0的情况。

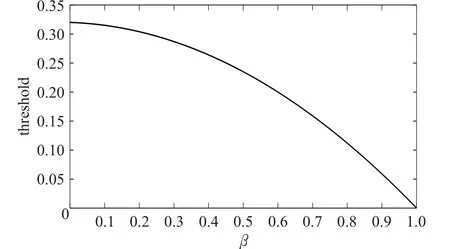
图3 算力阈值

本实验表明了当诚实节点拥有超过1 2系统的算力时并不能保证挖掘过程的绝对安全。为保证比特币挖掘协议在挖掘过程中的有效性，当β=0时，自私挖掘链的算力应小于0.3；当β=0.5时，自私挖掘链的算力应小于1 4。

4 结论

本文设计了自私挖掘区块的公布策略，给出一种基于概率的SAPV模型。首先详细分析了自私挖掘过程，基于此计算了挖掘过程的概率分布。该模型能通过优化自私挖掘池的绝对收益来提高自私挖掘的相对份额。实验表明该模型能有效提高自私挖掘的收益，能更严格地计算出保证诚实节点协议安全的算力阈值。限制自私挖矿池的算力是保证区块链系统进行安全挖掘的重要方法。在比特币挖掘系统中，针对自私挖掘池逐渐增大、挖掘算力浪费的问题，阈值的设定具有很好的防范作用。本文研究对挖掘协议的改进具有参考的价值。

但本文的研究仍有不足之处，本文选取的参数值需要进行多次调整以适应不同的场景，这方面有待于改进。构建基于多因素的自私挖掘分析模型有待下一步的研究与完善。