低渗透油藏中不同压裂注采井网非稳态产量计算分析
2018-08-01秦学杰苟斐斐方文超
蒲 军,秦学杰,苟斐斐,方文超
(1. 中国石化 石油勘探开发研究院,北京 100083; 2.中国科学院 渗流流体力学研究所,河北 廊坊 065007;3.中国科学院大学,北京 100190)
在井网压裂基础上进行注水开发,可以有效改善流场,增大泄油面积,提高油井产量与采收率,是改善低渗透油藏开发效果的重要手段[1-8]。快速准确预测低渗透油藏压裂井网注水开发产量可以为低渗透油藏开发优化设计奠定基础。但低渗透油藏注水开发呈现非稳态、非线性渗流特征,存在启动压力梯度[9-15],油水两相流动阻力大,基于达西定律形成的油藏工程方法并不适用。
针对这一问题,国内外油藏工程专家开展了大量的研究工作,但主要集中在室内实验及数值模拟方面,实验难度大、周期长,数学模型复杂、计算过程繁琐[16-23]。而中石化勘探开发研究院的计秉玉等人提出了流线积分法,通过分析流场内流线分布特征,将流场分解成多根微小流管,推导了低渗透油藏整体压裂条件下的油井产能解析计算公式,为低渗透油藏产能预测与评价提供了手段[24]。但该方法仍不完善,首先仅考虑了单相稳态渗流,无法计算注水开发过程中油井产量随时间的动态变化;而且只考虑了油水井同时整体压裂,不能对比分析不同压裂注采方式下油井产量的差异。
本文借鉴前人的研究经验,基于流线积分法建立了不同压裂注采方式下油水两相渗流的油井非稳态产量计算方法,计算并剖析了启动压力梯度、压裂注采方式及裂缝长度对油井生产动态的影响,可以为低渗透油藏压裂注采方式优选及注水开发对策制定提供依据。
1 不同压裂注采井网物理模型
根据增注或提产需求,油田现场一般有3种压裂注采方式:油井压裂、水井压裂和油水井同时压裂。不同压裂注采方式对流场的改造效果不同,油水井间呈现不同的流动特征,通过对压裂后的流场进行分析,油水井间的流动区域可以划分为不同的等效流动单元(图1)。
通过以上单元划分,不难看出不同压裂注采方式条件下油水井间存在4种流动单元类型:点源点汇流动单元、点源线汇流动单元、线源点汇流动单元及线源线汇流动单元。分别建立不同类型流动单元的产量计算模型,然后根据压裂注采方式将对应的流动单元产量相加即可得到不同压裂注采方式下的油井产量。
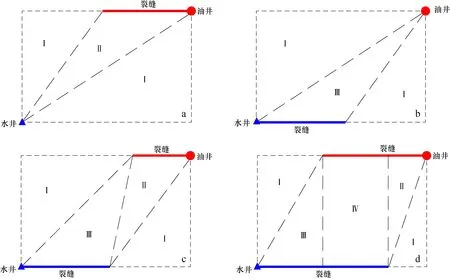
图1 不同压裂注采方式下流动单元划分Fig.1 Division of flow units under different fracturing injection and production modesa.油井压裂流动单元;b.水井压裂流动单元;c.油水井同时压裂(油井裂缝半长+水井裂缝半长≤井距之半);d. 油水井同时压裂(油井裂缝半长+水井裂缝半长>井距之半)Ⅰ.点源点汇流动单元;Ⅱ.点源线汇流动单元;Ⅲ.线源点汇流动单元;Ⅳ.线源线汇流动单元
2 不同生产方式下产量计算
2.1 流管非稳态水驱油理论
流场可以看作多根微小流管的集合,计算流动单元的产量首先需要建立单根流管的流量计算方法。假设地层等厚均质,渗流流体为油相与水相,地层与油水相均不可压缩。在参考文献[25]中,笔者已经采用流线积分法推导了注水开发条件下任意形态流管内的非稳态流量计算公式[公式(1)]。
(1)
式中:qo为流管油流量,m3/d;pe为注水井井底流压,MPa;pw为采油井井底流压,MPa;μo为油粘度,mPa·s;μw为水粘度,mPa·s;K为地层渗透率,10-3μm2;Φ为孔隙度,%;λ(2)为单相渗流区启动压力梯度,MPa/m;rw为井半径,m;λ(1)(x)为两相渗流区综合启动压力梯度,MPa/m;A(x)为流管截面积,m2;t为流动时间,s;L为流管长度,m;ξ为油水前缘位置,m;tf为油井见水时间,s;a,b,A,B,C为相渗常数。
对公式(1)中所有未知参数进行整理和分析,根据参数性质将未知参数分为3类(表1)。
2.2 流动单元产量计算
1) 流管特征参数计算
不同类型流动单元的特征参数计算方法推导过程基本相同,因此本文以点源点汇流动单元为例进行详细介绍,其他类型流动单元特征参数计算公式见表2。
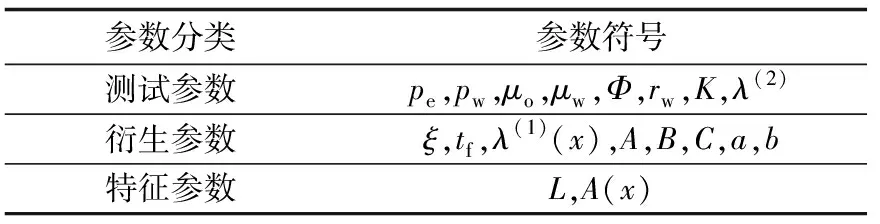
表1 流管非稳态产量计算公式中未知参数分类Table 1 Categories of unknown parameters in non-steadyproduction calculation of flow tube
注:测试参数是通过油田现场或室内实验测试获取的直接参数;衍生参数是通过计算才能获取的间接参数,笔者已经在参考文献[25]中给出了所有衍生参数的计算方法。推导出不同类型流动单元内流管的特征参数计算方法是计算不同流动单元流管流量的关键。
任意形态点源点汇流动单元及流管如图2所示。
① 流管长度L求解
基于图2建立三角函数关系方程,可以得到流管长度L如下:
(2)
式中:l为油水井距,m;α为流管与油水井连线夹角,(°);α0和β0为流动单元几何角,(°)。
② 流管截面积A(x)求解
在点源点汇流动单元中,流线会出现转折,流管截面积需要进行分段求解。通过几何分析可以得到点源点汇流动单元中流管截面积的计算公式如下:
(3)
式中:h为地层厚度,m;Δα为流管夹角,(°)。
2) 流动区域计算
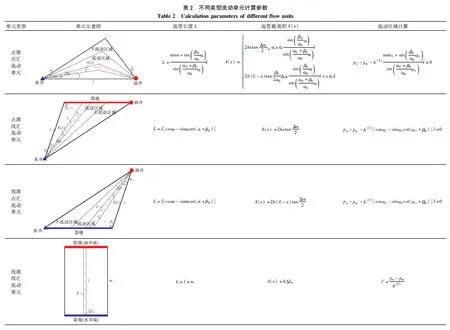
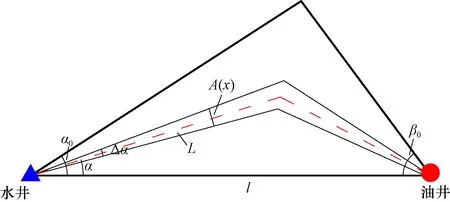
图2 任意形态点源点汇流动单元示意图Fig.2 Sketch map showing point source and point sink flow units
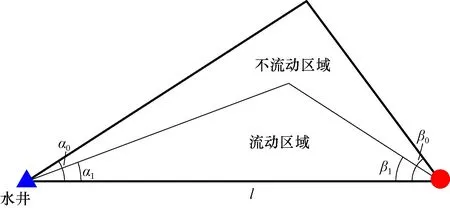
图3 点源点汇流动单元启动角示意图Fig.3 Sketch map showing startup angle of point source and point sink flow unit
由于低渗透油藏普遍存在启动压力梯度,在一定井距和注采压差条件下,点源点汇流动单元内的流体不一定都能参与流动,计算流动单元产量时需要首先确定流动区域。如图3所示,流动区域由特征参数-启动角控制,在参考文献[25]中,笔者已经给出了点源点汇流动单元启动角的详细计算方法。
根据图3,建立三角函数关系可以得到:
(4)
且
(5)
将公式(5)代入公式(4),可以得到关于启动角α1的三角函数方程:
(6)
式中:α1,β1为启动区域夹角,(°)。求解公式(6),可以得到点源点汇流动单元的启动角α1。得到启动角后,可以按照以下方法确定流动区域:
当α1≤0时,点源点汇流动单元全部不参与流动;
当0<α1<α0时,点源点汇流动单元部分参与流动;
当α1≥α0时,点源点汇流动单元全部参与流动。
按照相同的方法,很容易推导出点源线汇、线源点汇及线源线汇流动单元的流管特征参数及流动区域计算公式,形成流动单元计算参数表(表2)。
3) 流动单元产量计算
不同流动单元的产量可以通过如下步骤求解:①计算确定流动单元的流动区域;②将流动区域划分为多根流管;③根据油田现场及室内实验测试资料确定测试参数;④根据参考文献[25]中的方法计算衍生参数;⑤根据表2中的计算公式得到特征参数L、A(x);⑥将测试参数、衍生参数及特征参数代入式1,得到不同流管的油流量;⑦不同流管的油流量相加得到流动单元的产油量。
2.3 油井产量计算
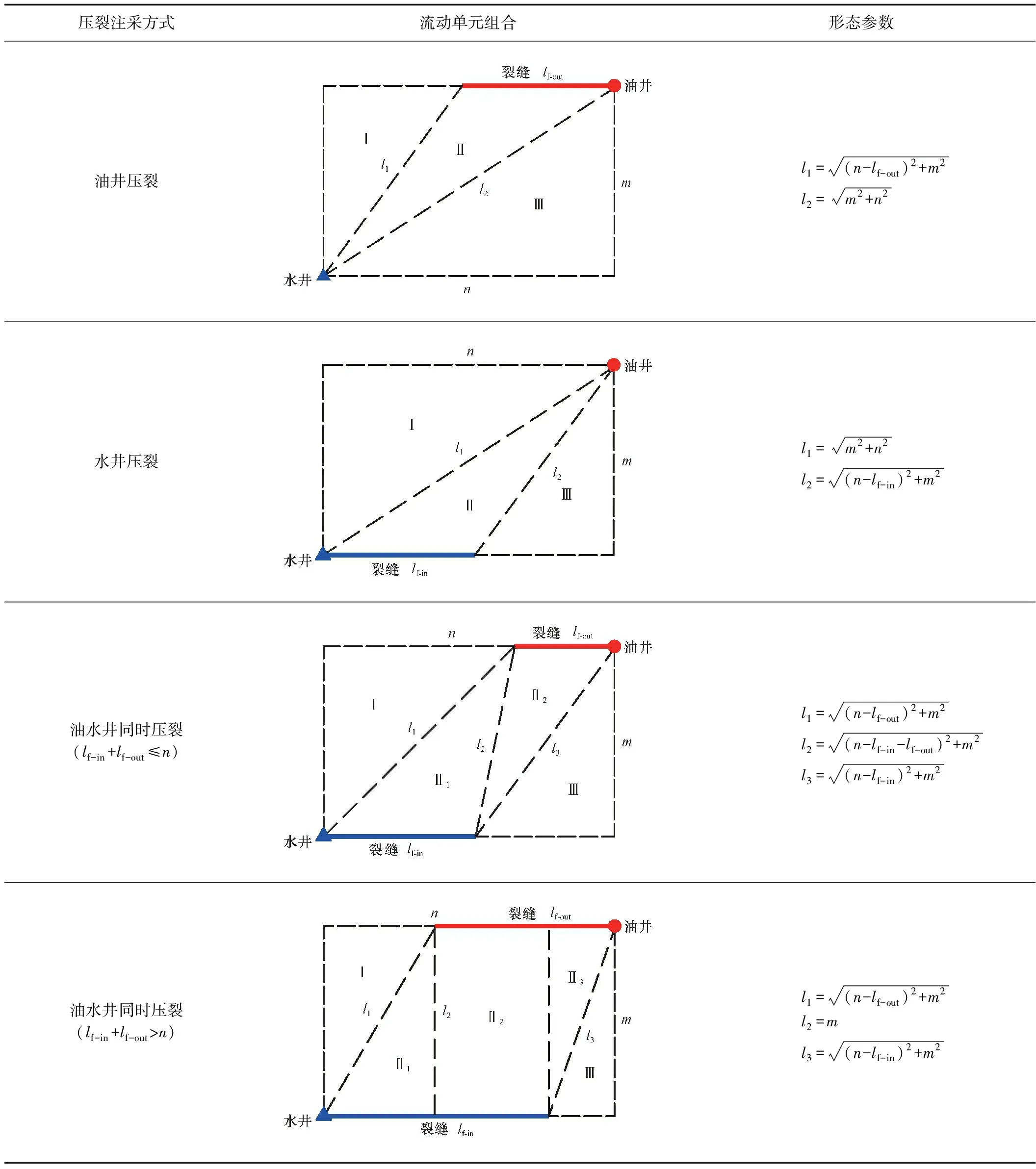
通过前面的分析可知,不同压裂注采方式下油水井间的流动区域可以划分为不同流动单元的组合,根据几何分析不难得到流动单元的形态参数(表3)。
令:
(7)
以油水井同时压裂方式(lf-in+lf-out>n,且l1>l3)为例介绍油井产量计算方法,其他压裂注采方式的油井产量计算基本相同,不再赘述。
① 当l′≤l2时,Ⅰ,Ⅱ1,Ⅱ2,Ⅱ3和Ⅲ单元均不参与流动,油井产量q=0;
② 当l2 ③ 当l3 ④ 当l′>l1时,Ⅰ,Ⅱ1,Ⅱ2,Ⅱ3和Ⅲ单元均参与流动,油井产量q=4(qⅠ+qⅡ1+qⅡ2+qⅡ3+qⅢ)。 以东部某低渗透区块为研究对象,该区块的基本参数见表4。在该区块采集了典型井的柱塞岩心,基于室内实验测试了该区块的油水相渗曲线和启动压力梯度曲线(图4),并开展了平板模型实验(定注采压差,Δp=2 MPa),实验模型及实验结果见图5。 表3 不同压裂注采方式下流动单元组合及形态参数Table 3 Flow unit combination and shape parameters under different fracturing injection and production modes 注:Ⅰ,Ⅱ,Ⅱ1,Ⅱ2,Ⅱ3和Ⅲ为流动单元编号,具体流动单元类型可以参考前面的分析结果。l1,l2和l3为流动单元形态参数,m;m为排距,m;n为井距之半,m;lf-out为采油井裂缝半长,m;lf-in为注水井裂缝半长,m。 表4 东部某低渗透区块基本参数Table 4 Parameters of a certain low-permeability block in the East China 图4 东部某区块油水相渗曲线与综合启动压力梯度曲线Fig.4 Relative permeability curves and composite threshold pressure gradient curve of a certain low-permeability block in the East Chinaa.油水两相渗透率曲线;b.油水两相流综合启动压力梯度曲线 图5 平板模型及产油量对比曲线Fig.5 Correlation curve of plate model and oil production a.平板模型示意图;b.产油量曲线对比(Δp=2 MPa) 为降低实验误差的影响,开展了5块物性相近的平板模型水驱油实验,对产油量曲线进行归一化平均处理;然后采用本模型计算了采出端的产油量曲线,与实验数据进行了对比(图5b)。通过对比可以看到,新模型的计算结果与实验结果基本一致,总体误差仅为4.35%,证明了模型的可靠性,可以满足工程应用。 1) 启动压力梯度的影响 假设井距为600 m,排距为200 m,裂缝半长为100 m,注采压差为15 MPa。计算了不同压裂注采方式下的油井累产油曲线,并取λ(1)=0及λ(2)=0为计算特例,对比分析了不同压裂注采方式下启动压力梯度对油井生产的影响(图6)。由图6可以看出,在低渗透油藏中,启动压力梯度增大了流体流动阻力,与不考虑启动压力梯度相比,流体流速慢,油井累产大幅降低,因此低渗透油藏中启动压力梯度不可忽略。 2) 压裂注采方式的影响 图6 不同压裂注采方式下启动压力梯度对油井累产的影响Fig.6 Effect of threshold pressure gradient on accumulative production under different fracturing injection and production modes 仍然假设井距为600m,排距为200m,油水井裂缝半长均为200m,注采压差为15MPa。根据前面介绍的方法,将不同压裂注采方式的油水井间流动区域划分为不同的流动单元,三种压裂注采方式一共有9个独立的流动单元(图7)。 图7 不同压裂注采方式下流动单元汇总Fig.7 Summary of flow units under different fracturing injection and production modesa.点源点汇流动单元;b.点源线汇流动单元;c.点源点汇流动单元;d.点源点汇流动单元;e.线源点汇流动单元;f.点源点汇流动单元;g.线源点汇流动单元;h.线源线汇流动单元;i.点源线汇流动单元 计算了各流动单元的产油量,对比了不同流动单元的油相渗流阻力、产油能力和见水时间(图8),进一步分析了不同压裂注采方式下流动单元对油井开发效果的影响。 其中,根据参考文献[26],定义油相渗流阻力如下: (8) 式中:Roil为渗流阻力,MPa·m-3·d;Δp为注采压差,Pa;qoil(t)为产油量,m3/d。 为对比各个流动单元的产油能力,定义流动单元的产油能力指数如下: (9) 式中:Ji为流动单元i的产油能力指数,m3/m2;Qi为流动单元i的累产;m3;Ai为流动单元i的泄油面积,m2。产油能力指数本质上指的是单位面积流动单元的累产。 通过图8可以看出:①不同流动单元的油相渗流阻力及其变化不相同,开发早期,流动单元8的油相渗流阻力最小,而流动单元4的油相渗流阻力最大,但是到了开发中后期,不同流动单元的采出油量不同,渗流阻力变化幅度不相同,此时流动单元3的油相渗流阻力最小,而流动单元9的渗流阻力最大;②不同流动单元的产油能力不同,流动单元8为线源线汇单元,原油流动距离短,油井端渗流面积大,产油能力最强,而流动单元4为点源点汇单元,原油流动距离远,油井端渗流面积小,产油能力最弱;③不同流动单元的见水时间不同,流动单元3和流动单元4面积大,流体流速慢,在计算期(180个月)都没有见水,而流动单元9见水最早,仅为24个月;④不同压裂注采方式产生不同的流动单元组合,而不同流动单元的产油能力完全不同,受此影响,不同压裂注采方式的增产效果也不一样,增产效果最好的是同时压裂注采方式,与完全不压裂相比,能够增产3.1倍;⑤不同压裂注采方式下,油井见水时间由最早见水的流动单元控制,因此油井压裂、水井压裂及同时压裂的见水时间与流动单元1、流动单元6及流动单元9相同,分别为42,43,24个月。 图8 不同流动单元油相渗流阻力、产油能力指数及见水时间对比Fig.8 Comparison of flow resistance of oil phase,oil productivity index and breakthrough time of different flow unitsa.不同流动单元油相渗流阻力对比;b.不同流动单元产油能力指数对比(180个月);c.不同流动单元见水时间对比 3) 裂缝长度的影响 仍然假设井距为600 m,排距为200 m,注采压差为15 MPa,计算了不同油水井裂缝长度条件下油井的产油量曲线(图9),分析了裂缝长度对油井产量的影响。 图9 不同裂缝长度下油井产量对比(不同压裂注采方式)Fig.9 Comparison of well productivity with different fracture lengths(different fracturing injection and production modes) 由图9可以看出:①随着裂缝长度的增加,流场改善程度越高,点源点汇流动单元越小,流动阻力越低,油井产油量越高;②油井累产并未随裂缝长度的增加而线性增长,存在最佳裂缝半长,当压裂缝长超过最佳裂缝长度,增油效果并不显著,经济效益反而变差。 1) 根据不同压裂注采方式对流场的改造效果划分等效流动单元,建立了不同类型流动单元特征参数及流动区域计算方法,形成了不同压裂注采方式的油井产量计算模型;通过与室内平板模型实验进行对比,验证了模型的可靠性,能够满足工程应用。 2) 启动压力梯度增大了渗流阻力,流体流速慢,与不考虑启动压力梯度相比,油井累产降低,因此,在低渗透油藏产量计算时应该考虑启动压力梯度的影响。 3) 不同压裂注采方式下油井的生产动态主要受流动单元所控制,不同流动单元内油相流动阻力、产油能力及见水时间差异大,导致不同压裂注采方式的开发效果完全不同。 4) 无论采用哪种压裂注采方式,随着裂缝长度的增加,油井产油量越大;但压裂存在最佳裂缝长度,当压裂缝长超过最佳裂缝长度,增油效果不明显,经济效益反而变差。3 验证与计算
3.1 模型验证

3.2 计算与讨论
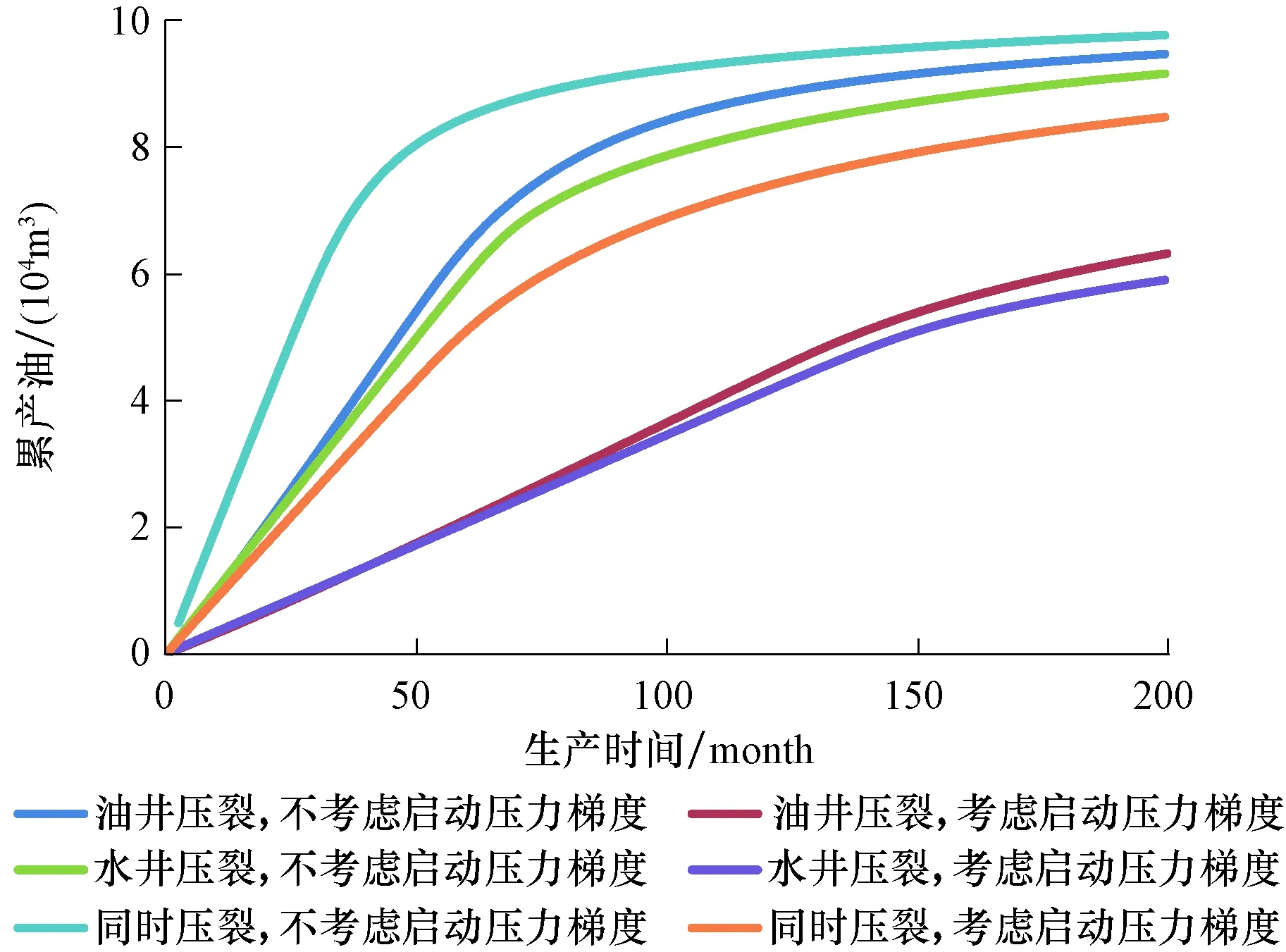
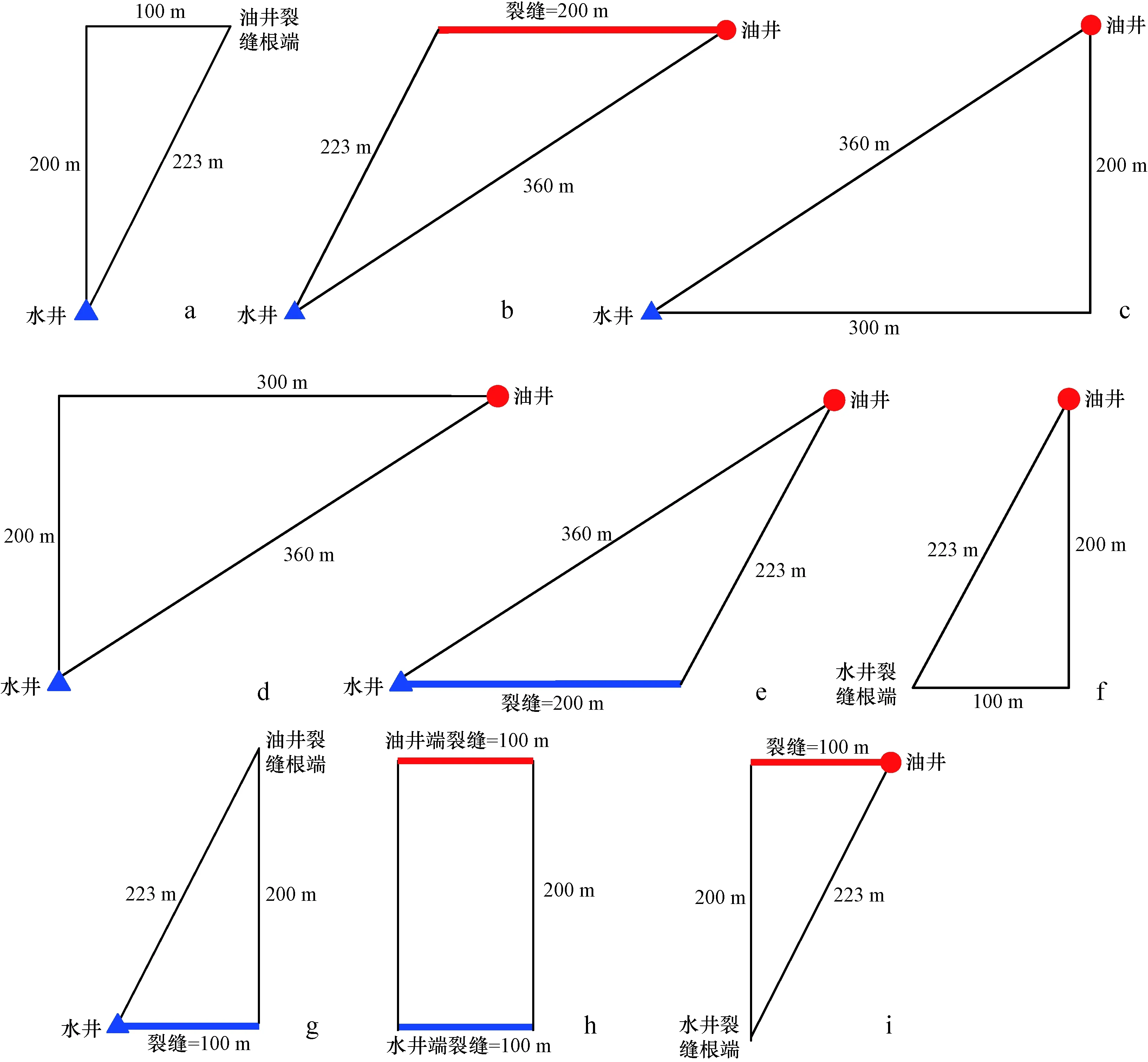
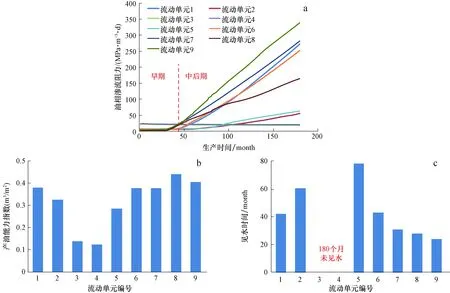
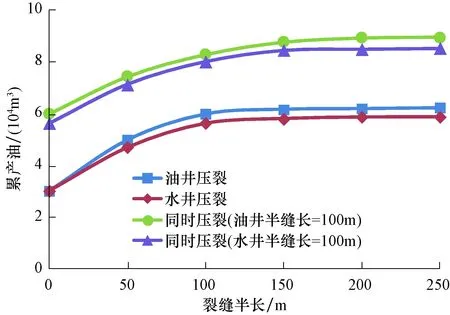
4 结论
