裂缝性储层分级评价中的卷积神经网络算法研究与应用
2018-08-01吴正阳莫修文柳建华胡国山
吴正阳,莫修文,柳建华,胡国山
(1.吉林大学地球探测科学与技术学院,吉林长春130026;2.中国石油化工股份有限公司西北油气分公司,新疆乌鲁木齐830011)
裂缝性碳酸盐岩和火成岩储层是油气勘探的重要目标之一,而裂缝则是其主要储集空间和渗流通道,有的还伴有溶蚀孔洞。因此,此类储层测井解释的主要任务之一是有效地识别裂缝并对其进行准确评价。裂缝性储层的解释分为定性和定量两个层次,定性解释是识别裂缝并对裂缝储层做出分级评价;定量解释则是对裂缝的长度、宽度、裂缝孔隙度[1]等进行定量计算。由于裂缝性储层的非均质性非常强,测井响应特征受各种因素的影响而变得极为复杂,导致有些裂缝性储层的异常特征不明显。因此,裂缝的识别和分级评价是此类储层测井解释的一个难点。
前人从不同角度对裂缝识别问题进行了大量探究,如韩磊等[2]利用综合密度法、判别分析法、改进的BP神经网络法对裂缝存在与否进行评价;瞿子易等[3]利用粒子群和支持向量机的方法对裂缝进行了识别;ZHANG等[4]引入小波变换的方法建立了裂缝指示曲线;TAN等[5]利用三维有限元数值模拟法模拟双侧向测井的裂缝响应特征。在裂缝发育程度及其分级评价方面,汤小燕等[6]利用综合概率法对火山岩裂缝发育程度进行了评价;郭秀娟等[7]利用分维方法描述了裂缝的发育程度;张立松等[8]等根据Griffith准则和Hoek-Brown准则确定了定量表征裂缝发育等级的参数;徐平等[9]在克深地区利用裂缝孔隙度、裂缝渗透率等参数建立了裂缝发育等级评判表。
可以发现,裂缝性储层的分级评价仍然以常规测井资料为主。近年来,成像测井资料的应用越来越广泛,为判别裂缝发育程度提供了具有很高参考价值的井眼图像资料。但无论是利用常规测井资料还是成像测井资料,目前的解释方法仍然需要人工选取或求解多种参数,而且普遍存在效率低、受经验性和主观性影响容易导致误判等问题。因此有必要寻求一种受参数不确定性影响小、裂缝评价的准确性更高且更具识别效率的判别裂缝发育等级的方法。
卷积神经网络算法是一种用于图像辨别和语音研究的高效深度学习方法[10]。该算法无需建立测井解释模型或计算各类反映裂缝特征的参数,网络会自动寻找不同等级的裂缝与测井响应数据之间隐含的、甚至难以用数学公式表达的关系。因卷积神经网络具有局部连接与权值共享等特点,可以更高效、更全面地提取输入信息的特征去寻找最优解,而且能够避免普通神经网络算法容易过拟合和陷入局部最优解的缺陷,所以本文引入卷积神经网络技术对不同发育程度的裂缝进行识别。
1 裂缝发育等级判别标准及方法
1.1 裂缝发育等级判别标准
裂缝性储层的基质孔隙度极低或不发育,其油气的储集空间和渗流通道主要是裂缝,故裂缝的发育程度直接影响到储层的品质和产能。但裂缝系统本身的复杂性会导致储层强烈的非均质性,因此基于常规测井的传统解释方法难以对其进行准确识别和评价。经过大量实践,前人对裂缝性储层的测井响应特征有了较全面的认识,提出了利用电阻率测井、孔隙度测井以及成像测井的某些特征判别储层的裂缝发育程度的方法[11-13],并据此将裂缝分为4类[14-15]。其判别标准大致可以总结为:Ⅰ类储集层,裂缝极发育,裂缝密度大、张开度好,具有全井段相对最好的渗透性,为主要的储、渗空间,测井曲线上,裂缝响应特征明显;Ⅱ类储集层,裂缝发育中等或一般,裂缝密度较大,具有全井段相对较好的渗透性,在测井曲线上有较明显响应;Ⅲ类储集层,裂缝发育一般,裂缝密度较小,具有全井段相对较差的渗透性,测井曲线上裂缝特征不明显;Ⅳ类储集层,为裂缝不发育的致密层,测井曲线上无裂缝显示[16]。这种分类已经在我国多个探区的碳酸盐岩储层勘探生产中得到应用。
1.2 裂缝发育等级判别方法
要得到更准确的裂缝分级评价结果,往往需要综合常规测井资料、成像资料和钻井现场资料等多种资料[17]。但实际生产中,很多情况下只能依赖于常规测井资料,在此基础上发展的综合概率模型是判断裂缝发育程度的主要方法。该方法综合利用多种测井资料判别裂缝,依据各条测井曲线反映的裂缝特征,提取测井裂缝指标并计算其指示裂缝存在的概率,最后通过加权计算建立综合概率模型划分裂缝带[18]。
用以指示裂缝的指标主要有裂缝孔隙度Φ、裂缝开度ε、孔隙胶结指数m、次生孔隙度指数Φ2、井径指标DCAL、自然放射性铀异常PU、井温指标DMP等。将裂缝指标进行正态转换之后,利用指数函数建立裂缝概率函数,并根据加权平均的思想得到综合概率模型:
(1)
式中:P为综合概率;Pj为第j种测井方法的裂缝概率;Wj为对应的权值。
裂缝孔隙度指标主要利用深、浅侧向测井曲线的幅度差计算得到,如果有微电阻率成像测井资料,则计算效果更好。因泥浆侵入与裂缝孔隙度有较大相关性,而双侧向测井可以指示泥浆的侵入情况,故可以利用双侧向测井曲线的幅度差来估算裂缝孔隙度[19]。在泥浆侵入时,侵入带裂缝中的流体会先于基质中的流体被泥浆滤液替代,此时深、浅侧向电阻率可表示为:
式中:φm,φf分别为基质孔隙度和裂缝孔隙度;Swf,Swm分别为原状地层裂缝的含水饱和度和基质部分的含水饱和度;m,mf分别为基质和裂缝的胶结指数;n,nf分别为基质和裂缝的饱和度指数;Sxof为冲洗带裂缝含水饱和度。
据此可计算出含油层及含水层的裂缝孔隙度:
式中:Rmf为泥浆滤液电阻率;C浅,C深分别为浅侧向和深侧向测得的电导率;Cmf,Cw分别为泥浆滤液和地层水的电导率。
用微电阻率成像资料也可以计算井壁孔隙度,其原理是根据阿尔奇公式将电阻率图像转为孔隙度图像。首先,将该方法测得的电阻率视为冲洗带电阻率,其含水饱和度Sxo=1,设阿尔奇公式中的参数m=n=2,a=1,则孔隙度可以用电阻率表示为:
(6)
式中:Rxo为冲洗带电阻率。根据孔隙度图像,可进一步给出孔隙的分布和大小。如果孔隙度频率图出现单峰,说明此深度段只有原生孔隙;若显示双峰或多峰,表明存在次生孔隙,如裂缝等。
可以看出,判别裂缝储层的等级不仅需要人工综合分析多种测井资料,还需要计算多个与裂缝相关的参数,工作量大、效率低,而且如果参数或模型选择不当,会使结果产生偏差或增加不确定性。而卷积神经网络技术只需输入多条测井曲线,无需很多的中间环节和人为干预,不仅能同时利用多种测井方法,还可优势互补,找到比较全面的各个裂缝等级特征,实现裂缝准确分级的目的。
2 卷积神经网络算法及其实现过程
卷积神经网络(CNN)是多层感知器(MLP)的生物启发式变体[20]。根据生物神经网络的特点,提出了具有稀疏连接和权值共享特质的卷积神经网络。作为目前最流行的深度学习算法之一,卷积神经网络在图像特征提取领域已经得到广泛应用,王秀席等[21]利用改进的卷积神经网络LeNet-5进行车型识别,GOLOVKO等[22]将卷积神经网络应用于手写数字分类问题,都取得了较好的结果。但是目前还未见到应用于裂缝识别的文献。
2.1 基本原理
卷积神经网络是一种特殊的深层神经网络模型,它的建立基于3个重要的架构概念:局部连接、权重共享和子采样。局部连接是指隐层的每个神经元不必感受全部的输入信息,只提取局部区域的信息,如图1所示,每个神经元只与对应图像位置的感受野相连接。这种结构将学习到的信息限定在局部空间里,降低了毗邻层神经元之间的连接数量,亦即减少了需要训练的参数个数。经过多层堆叠之后,卷积神经网络就可以得到全局的信息[23]。权重共享指的是隐层的所有神经元共用权值参数和偏置参数,也就是使用同一个卷积核提取输入层的一种特征,进一步降低参数数量。为获取输入层的多种细节信息,我们可以使用多个卷积核去卷积图像。子采样是对提取的信息进行简化,保留有用信息的同时减少数据处理量。

图1 局部连接示意
2.1.1 卷积神经网络的结构
卷积神经网络通常由输入层、卷积层、子采样层、全连接层和输出层组成,其结构如图2所示,3个卷积核分别与输入图像进行卷积得到卷积层C1的3个特征图,然后对卷积层C1进行子采样,得到3个子采样层S1的特征图。同理,子采样层S1与8个卷积核分别再进行卷积,然后经过子采样,得到卷积层C2和子采样层S2。最后,将提取的特征铺开连接成一个向量送入全连接层进行处理,得到最终输出。
2.1.2 卷积层
卷积操作具备局部连接和权值共享的特征。卷积过程如图3所示,卷积核的每个元素与输入图像的对应位置相乘再求和,然后将卷积核向右移动一个单位,再次进行卷积,直到完成对整张图的卷积操作。
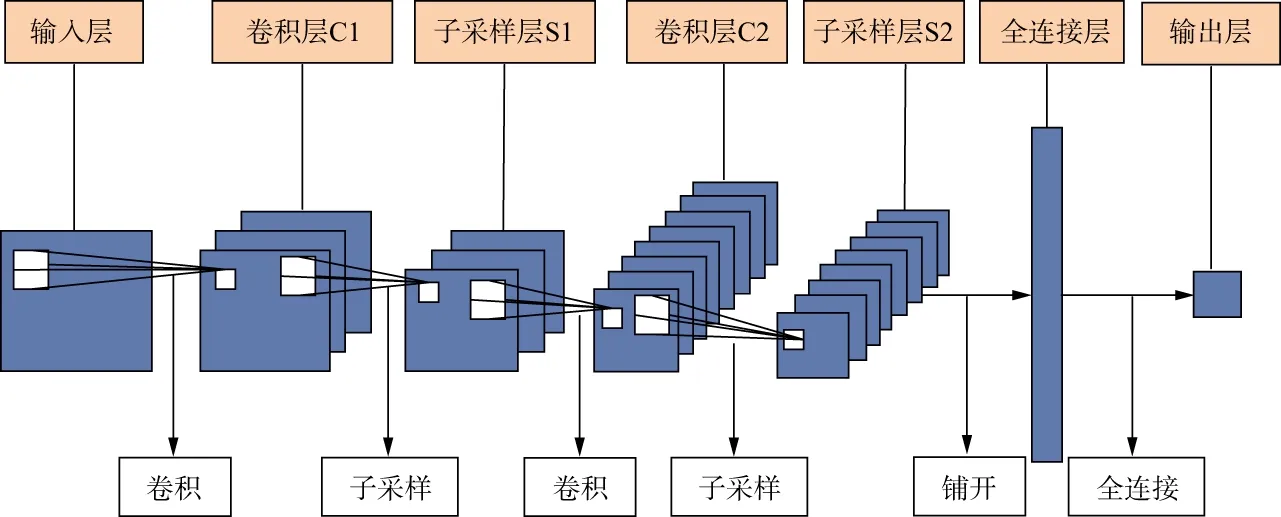
图2 卷积神经网络结构示意
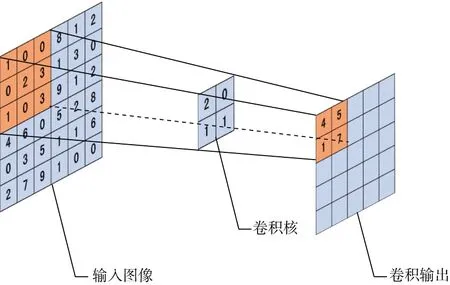
图3卷积过程示意
卷积完成后,在其结果上加一个可以训练的参数即偏置(bias)。因之前都为线性操作,为使卷积神经网络模型具备拟合非线性特征的能力,需要引入一个非线性的激活函数对得到的结果进行处理,本文采用ReLU函数。
经该函数映射后得到卷积层的输出特征图。具体卷积过程如公式(7)所述。
(7)
式中:outputi为第i个卷积核的输出;inputk为卷积层的第k个输入;ωi为第i个卷积核的权重;bi为第i个卷积核对应的偏置;f[·]为激活函数;conv(·)为卷积操作。
2.1.3 子采样层
子采样层通常在卷积层之后,根据输入信息局部相关性,对特征图进行子抽样,减少特征图和网络中超参数的个数。常用的子采样方法有:最大值子采样和均值子采样。如图4所示,将卷积层的每个特征图划分成几个不重叠的小区域,分别求取各个区域的最大值或平均值,将这些最大值或平均值投入到后续的训练。除此之外还有运用高斯模糊方法的高斯子采样和可训练子采样。
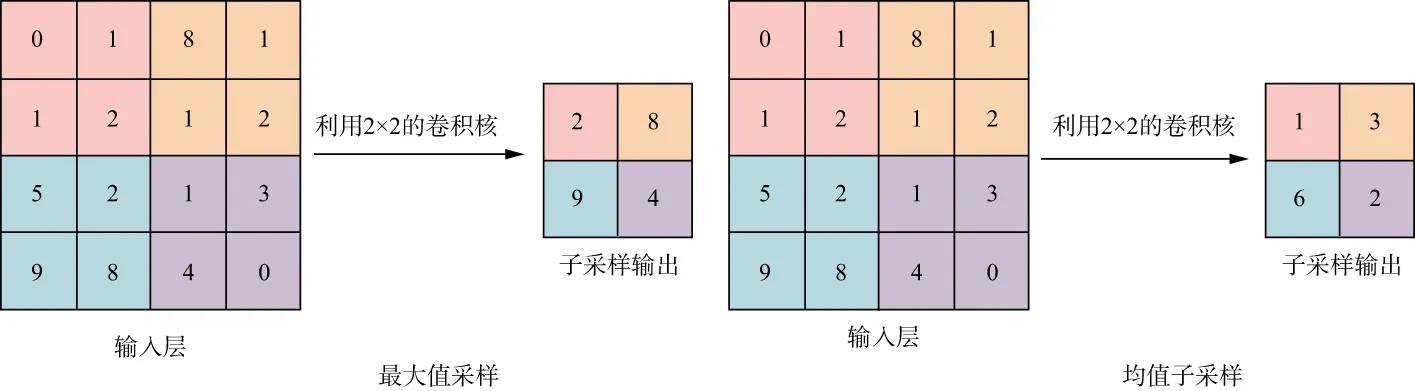
图4 子采样过程示意
2.2 卷积神经网络的实现过程
用于裂缝发育程度识别的卷积神经网络模型由输入层、卷积层、全连接层和输出层组成。针对所选研究区域地质和测井概况,选取与裂缝具有较大相关性的测井曲线资料以及裂缝判别资料。对其进行预处理之后,选取不同发育等级的裂缝和与之对应的测井数据构成学习样本和检验样本。
训练网络时输入层为一列测井数据,之后排布3个卷积层。第1个卷积层通过15个1×2×1的卷积核,分别提取测井数据与裂缝之间隐含的关系特征。第2个卷积层由20个1×2×15的卷积核组成,第3个卷积层由25个1×2×20个卷积核组成,分别抽取上层提取的特征的组合特征。然后将提取的组合特征变为一个向量输入全连接层,最终输出网络预测的裂缝发育等级。
采用小批量梯度下降法,batch-size为40,当输入的训练样本数达到40时,批量求取预测结果与已知的裂缝发育等级之间的误差。并将此误差在网络中进行反向传播,依次得到全连接层、卷积层的权值和偏置的梯度,并据此更新每个参数。反向传播结束后进行下一批次的训练。当训练次数达到设定的最大迭代次数10000时,训练结束并得到确定的网络模型。将本井与邻井的测井数据依次输入该模型,得到裂缝发育程度的预测结果并与综合概率法或成像测井结果进行对比和解释。模型的实现流程如图5所示。
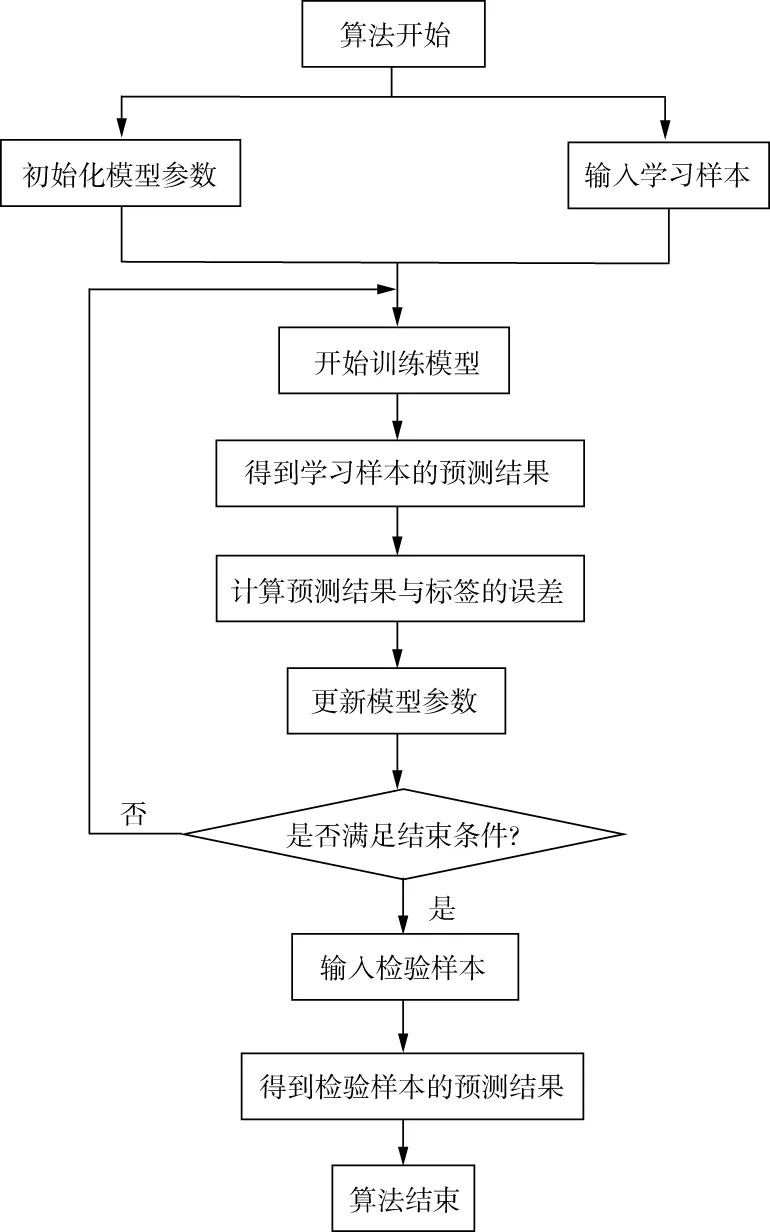
图5 卷积神经网络模型应用流程
3 实际应用与效果分析
利用本方法,对塔里木盆地北部某含油气构造单元裂缝性储层进行了储层评价。该区域地层形成时代为震旦系—新生界,油气储层以裂缝性碳酸盐岩地层为主,岩性多为白云岩以及石灰岩[24]。研究区地层致密,在构造运动等地质作用的影响下发育了大量的裂缝、溶洞等次生储集空间。
3.1 数据准备
研究区测井资料以常规测井资料为主,且对部分井裂缝发育情况的研究程度已经比较深入。因此,以某些有代表性的关键井和重点层段作为裂缝分级评价的标准样本,经过优选敏感曲线,提取了不同发育程度的裂缝响应特征。
3.1.1 输入测井曲线类型的选择
选取了对裂缝较为敏感的井径、声波、中子、密度、自然伽马、浅侧向、深侧向测井曲线作为网络模型的输入。
1) 井径曲线。
裂缝有时会使得井径扩大或产生椭圆井眼;若钻井过程中使用了堵漏材料,还可能造成井径因堵漏材料的堆积而减小。
2) 声波测井曲线。
一般认为声波速度反映的是基质孔隙度,但也可能与裂缝产状有关。水平裂缝发育时,纵波的能量会因反射和折射而有所衰减,时差会增大,声波曲线上有时会出现周期“跳跃”现象;横波在遇到裂缝时速度下降更加明显。
3) 中子测井曲线。
中子测井反映的是地层的含氢指数,在裂缝地层会有泥浆侵入,含氢指数上升,使中子孔隙度有所增加。
4) 密度测井曲线。
密度测井输出的泥饼校正曲线Δρ有时可用于指示裂缝的存在。当井眼规则,裂缝岩石边缘被钻头削落时,Δρ曲线会显示出比正常情况更高的校正值,而密度测井仪会显示明显的低密度值。
5) 自然伽马测井曲线。
在裂缝发育层段,地下水的流动可能会伴随一定量的铀沉积,导致自然伽马曲线出现明显高值。
6) 双侧向测井曲线。
侧向测井发出的电流在地层中呈水平辐射状,探测深度不同的两条双侧向曲线受裂缝影响程度不同。高角度裂缝发育时,深浅侧向测井曲线会出现正幅度差;而在低角度裂缝发育段深浅侧向测井曲线会产生负幅度差或重合[25]。
3.1.2 训练数据和检验数据的选择
对研究区多口井的测井数据、地质录井和取心资料进行综合分析可知,裂缝和溶洞主要发育在奥陶系地层,从中选取训练数据和测试数据。训练数据来自于多口井,共897组,其中Ⅰ类储集层(裂缝发育)数据158组,Ⅱ类储集层(裂缝较发育)数据430组,Ⅲ类储集层(裂缝欠发育)数据35组,Ⅳ类储集层(致密层)数据274组。为了检验方法的有效性,选择STK69,STK311等数口井进行了测试,即测试数据集与训练数据集不重合。
3.1.3 数据预处理
将测井数据输入网络之前需要进行预处理,首先对数据进行归一化处理:
(11)
式中:B*为归一化后的各类测井曲线;B为各类原始
输入曲线;Bmax为输入的各类测井曲线的最大值;Bmin为输入的各类测井曲线的最小值。
然后对裂缝等级数据进行量化处理,定义为Ⅰ类储集层为1,Ⅱ类储集层为2,Ⅲ类储集层为3,Ⅳ类储集层为4。
3.2 裂缝发育等级识别结果对比与分析
图6显示了STK69井5507.0~5559.5m裂缝发育等级判别结果,可以看出:在5507~5518m井段,自然伽马值明显升高,井径较大,中子孔隙度和声波时差高于其它层段,出现低密度值,深、浅侧向电阻率值很低,为小幅度的正幅度差或重合,具有Ⅰ类储集层即裂缝发育的特征,卷积神经网络和人工解释结论都给出了正确的判断结果;在5518~5530m,自然伽马值较大,井径较小,中子孔隙度和声波时差较高,密度没有明显降低,深、浅侧向电阻率较低,略高于裂缝发育层段,两类方法都判断为Ⅱ类储集层;在5530~5546m井段,自然伽马值较低,井径较大,中子孔隙度与声波时差都很小,密度没有减小的趋势,深、浅侧向虽有较大幅度差但电阻率测量值都很高,综合判断为Ⅳ类储集层即致密层;5546~5547m处,深、浅侧向测井值在高电阻率的背景下明显下降且有较大幅度差,判断为Ⅰ类储集层,但两种方法判断的层厚略有不同;5558~5560m,双侧向测井电阻率值明显下降呈较小幅度差,判断为Ⅲ类储集层。
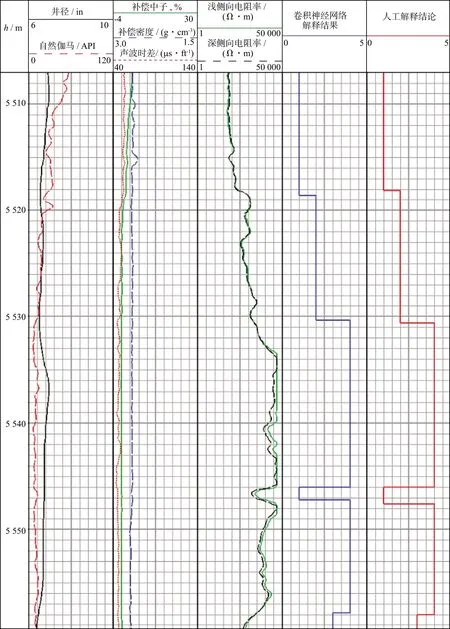
图6 STK69井5507.0~5559.5m裂缝发育等级判别结果(1in≈2.54cm,1ft≈0.3048m)
图7为邻井STK311井的判别结果,卷积神经网络算法和人工解释的结论很相近,判断的不同类别的储集层的厚度略有不同。5450~5470m深度段,自然伽马值稍有增高,井径值整体较小,声波时差稍有增大,密度值略微减小,深浅侧向电阻率值较低,略有幅度差,仅在5462~5463m,井径较大、声波时差略有减小、密度值稍有增大,且电阻率值明显增高,因此人工解释将5461.8~5463.0m判断为Ⅳ类储集层,卷积神经网络判断的致密层厚度略薄,5450~5470m其余深度段,两种方法都判别为Ⅱ类储集层;在5486~5498m深度范围内,自然伽马值较大,声波时差明显升高,双侧向测井电阻率值降低且有较大的正幅度差,两种方法都判断为Ⅰ类储集层。
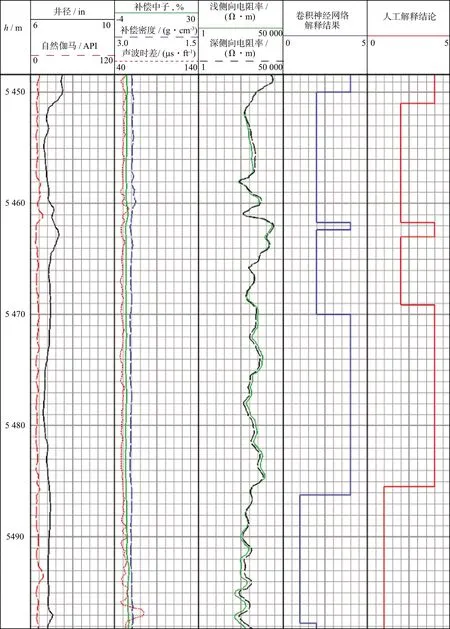
图7 STK311井5448.375~5498.375m裂缝发育等级判别结果(1in≈2.54cm,1ft≈0.3048m)
对比两种方法对STK69井、STK311井的裂缝分级结果,可以看到,卷积神经网络算法的解释结果与人工解释结论的符合率很高,除个别裂缝段的边界稍有差异,对各层段裂缝发育级别的判断结论基本一致,且卷积神经网络算法减少了很多中间环节,避免了更多人为因素的干扰,运行效率更高效便捷。
4 结论与认识
1) 卷积神经网络的多层网络多个卷积核、权重共享、非全连接等特性,使网络运行速度较快且不易陷入局部最优值。
2) 利用卷积神经网络算法对裂缝性储层进行分级评价时,可以充分利用测井曲线中有关裂缝特征的信息,且提取过程是客观的,不受人为因素的干扰,减小了人工造成的判断误差和计算误差。
3) 卷积神经网络算法对裂缝发育程度的判断与其它方法得到的结果相比,具有很好的一致性,但效率更高,使用更方便,它可以作为现有方法的有效补充,提高测井解释的效率,具有一定的推广价值。
4) 学习样本的选取对于裂缝的分级结果有较大影响,需要挑选与测试井相关性较强的已知井,并从中提取训练数据。
