AR模型的谱分辨率及小信噪比下的性能分析∗

刘晞远 胡昊颖 吴 珊 郭万里

（西安电子科技大学通信工程学院 西安 710126）

1 引言

谱估计的主要方法有非参数化法和参数化法，或称经典谱估计方法和现代谱估计方法。经典谱估计方法是以傅立叶变换为基础的，虽然具有计算效率高的优点，但它没有将信号的可用信息结合到估计过程中，有着频率分辨率低和旁瓣泄漏严重的固有缺点［1］。现代谱估计的一个重要方法就是将被观测过程表示为一个AR过程，通过对过程参数的估计，可以直接计算其功率谱密度。该方法可以获得更精确，频率分辨率更高的谱估计［2］。

2 AR模型现代谱估计

2.1 AR模型的建立［3］

现代谱估计的方法一般按照以下三个步骤进行：1）为被估计的随机过程确定或选择一个合理的模型，这种选择可能是基于有关信号是如何产生的先验知识；2）根据已知观测数据估计模型的参数；3）用估计得到的参数代入模型参数估算功率谱。

一个AR过程x(N)可以表示为单位方差白噪声驱动的全极点滤波器的输出。p阶AR过程的功率谱是［4］

在实际应用中，常需根据信号的有限个取样值来估计AR模型的参数，求其参数的方法主要有：Yule-Walker法或自相关法；协方差法；Burg法；修正的协方差法。以上方法都可以用由时间平均代替集合平均的最小平方准则推导得到。

2.2 AR模型参数估计的典型算法

2.2.1 自相关法［5］

自相关法是直接估计AR参数。用最小平方时间平均代替集合平均准则，有

自相关法的计算效率高，且能保证预测误差是最小相位的，但数据两端要附加零取样值，实际上等效于数据加窗，这将使参数估计的精度下降。特别是当数据段很短的时候，加窗效应就更为严重。

2.2.2 Burg算法［6］

Burg法与自相关法不同，它不直接估计AR参数，而是先估计反射系数，然后利用Levinson递推算法由反射系数求得AR参数。Burg法在希望利用已知数据段两端以外的未知数据的同时，又设法保证了使预测误差滤波器是最小相位的［7］。因此，Burg算法是基于 Levinson-Durbin［8］递推公式，对误差序列的最小化准则进行修正的AR模型参数估计法。

Burg法首先要估计反射系数，使用的准则是前项和后项预测误差功率估计的平均值最小准则（预测误差功率估计用时间平均代替集合平均）。因此，Burg法估计反射系数的准则表示

该式的前项和后项预测误差滤波器的工作都是在数据段上进行的（数据段两端不需要补充零）。

2.3 AR谱估计的异常现象

1）虚假谱峰［7］

如果自相关函数的取样值或反射系数值的估计没有误差，那么AR（p）模型参数的估计值在理论上应该为

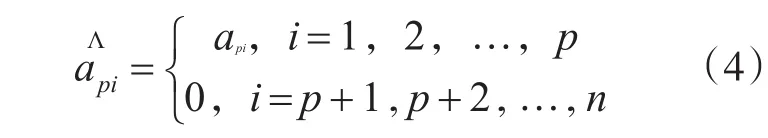
式中，api是AR（p）模型的精确参数值，是其估计值。但是实际上自相关函数或反射系数的估计是有误差的，一般来说，这就有可能使得对于大于p的i值有≠0，相应的将会产生n-p个额外的极点。若这些额外的极点出现在单位圆附近，就会形成虚假的谱峰。

2）谱线分裂［8］

如果要估计的随机过程是由一个正弦信号叠加噪声所构成，那么AR谱估计中谱峰出现的位置与正弦信号的初相位有着密切关系。而对于某些算法，还会观察到AR谱估计中存在两个靠的很近的谱峰，似乎在随机过程中还存在着另一个正弦信号。这一现象称为谱线分裂。

其中，Burg算法可以观察到AR谱估计出现谱线分裂现象。由经验总结出，在以下几种情况下最容易发生谱线分裂现象［9］：（1）高信噪比；（2）正弦分量的初始相位为45°的奇数倍；（3）数据序列长度为正弦分量1/4周期的奇数倍；（4）估计的AR参数的数目与数据的个数相比占有较大的百分比；（5）虚假谱峰常伴随产生谱线分裂现象，这与数据记录长度太短有关。因此，增加数据记录长度，这种现象便随即消失。

2.4 模型阶数的选择［10］

在AR谱估计中，模型阶次的选择是一个关键问题。阶次太低将会导致过于平滑的谱估计结果，频率分辨率过低；而阶次太高，将会产生虚假谱峰，并且估计的方差也会增大。文中采用最终预测误差准则（FPE）判断最优阶次。该准则的计算公式为［11］

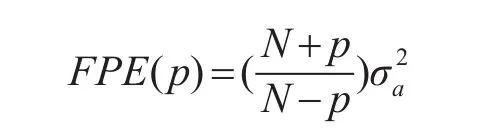
其中：N为数据点数；p为待估计参数，对AR（n）模 型 ，p=n；σa2为模型残差。

文献指出，估计阶次的上界L与样本长度N之间的关系为［12］，但文中既没有给出理论推导，也没有给出实际验证。通过实验研究表明，将样本长度的均方根值作为滚动轴承AR模型的定阶上界，可以得出满意的AR模型分析结果。

3 Levinson算法和Burg算法下的AR模型的谱分辨率性能分析

AR模型功率谱估计性能，可以用Matlab仿真实现。本文仿真选取采样点数为256（中等长度的数据），采样频率为100的信号。为了深入研究两种算法的谱分辨率性能，采用下列自编程序代替Matlab内置函数在Matlab上进行了仿真，如下：

3.1 预测阶次p对两种算法谱分辨率的影响

1）预测阶次p对Levinson算法仿真结果的影响

使用Matlab仿真了F1=20Hz；F2=21Hz条件下不同频率对应的功率谱图，如图1～图5所示。

图1 p=5时

图2 p=10时

图3 p=20时

图4 p=56（N/4）时

图5 p=128（N/2）时

仿真结果显示：Levinson算法的分辨率较低，在p=20时分辨率才能达到1Hz；阶次越大，谱线的虚假谱峰现象越严重，图5中最大虚假谱峰已经达到-50dB；Levinson算法的仿真没有出现谱裂现象。

2）预测阶次p对Burg算法的影响

使用Matlab仿真了F1=20Hz；F2=21Hz条件下不同频率对应的功率谱图，如图6～图10所示。

图6 p=5时

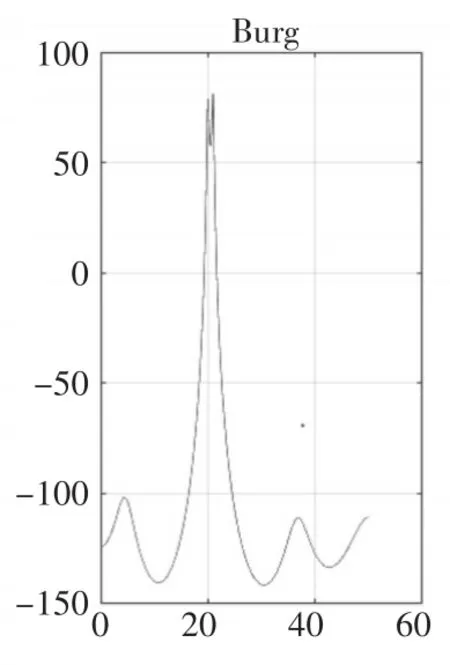
图7 p=10时

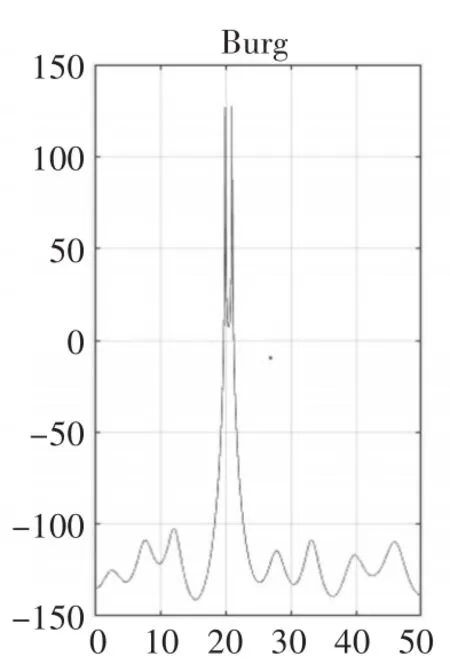
图8 p=20时

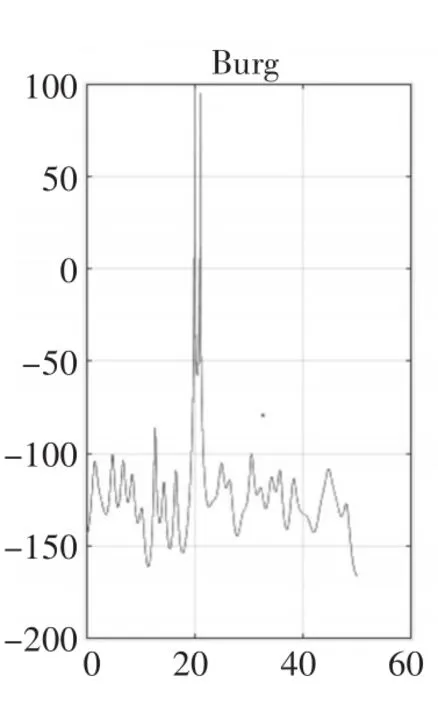
图9 p=56（N/4）时

图10 p=128（N/2）时

仿真结果显示：阶次较低时，Burg法与Levinson法性能相似，如图1与图7所示，但是随着阶次的提高，Burg法的谱峰比Levinson法更加尖锐，准确度更高，如图10和图11比图4和图5尖锐很多，但是虚假谱峰现象更加严重，谱线更加不稳定，毛刺较多，图11中p=N/2时出现谱裂现象，严重影响了Burg法的性能。

3.2 在不同的频率差下，两种算法谱分辨率的比较

图11（a）、（b）、（c）的信号是两个单频信号的叠加加上一个高斯白噪声（信噪比为10dB）的功率谱估计图。x=sin（2*pi*F1*n）+sin（2*pi*F2*n）+（1/20）*randn（size（n））

采样点数：256，采样频率：100。

图 11（a）、（b）、（c）分别为频率差为 3Hz、5Hz、1Hz时，两种方法在FPE最佳阶次准则下的AR模型功率谱图。

分析：

1）图11（a）所示，在相同的信号情况下，用FPE准则算出的Levinson最佳阶次比Burg算法的低。（不论俩个信号频差多少），在最佳阶次下，Burg算法的结果毛刺较多，功率谱的方差较大，而Levinson法的谱线相对平滑。

2）Levinson算法的分辨率比Burg低，在图（c）中两个信号频率差为1Hz，Levinson已经不能分辨。

3）图11（b）所示，Burg算法有谱裂现象，特别是当阶次较高时。所以FPE准则对于Burg算法预测的阶次偏高，应稍微降低阶次来减少谱裂，而对Levinson算法来说阶次偏低，应增加阶次来提高分辨率。

3.3 信号频率差与最佳阶次的关系

图12（a）、图12（b）分别是Levinson算法、Burg算法最佳阶次随频率差的变化图。

图11 两种方法在FPE最佳阶次准则下的AR模型功率谱图

分析：1）实验数据表明用FPE准则计算出的最佳阶次确实随着频率差的变换而变换。

2）对于Levinson算法，最佳阶次随頩差的变换曲线呈现单峰性质，在3Hz最有出现最大的阶次。而对于Burg算法，最佳阶次普遍偏高，且最佳阶次随頩差的变换呈现双峰特征。

3.4 信号频率差对AR模型预测误差的影响

分析：1）Levinson算法的误差较大，Burg算法的误差较小，这主要是由于Burg算法FPE最佳阶次准则中阶次较高引起的。2）与Levinson相比，Burg法的误差变化相对较小，预测精度比较稳定。

图12 两种算法最佳阶次随频率差的变化图

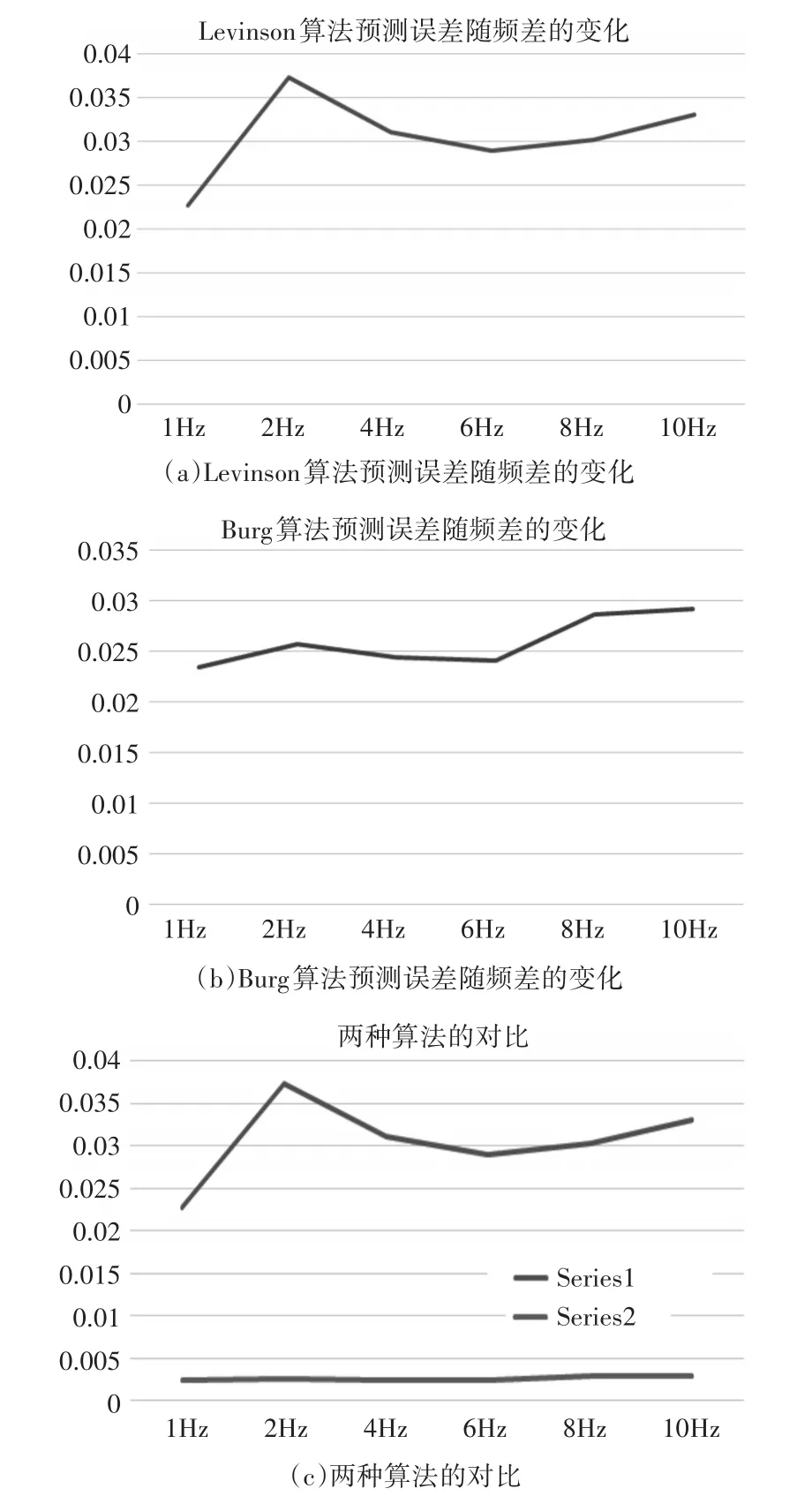
图13 两种算法预测误差随频差的变化图

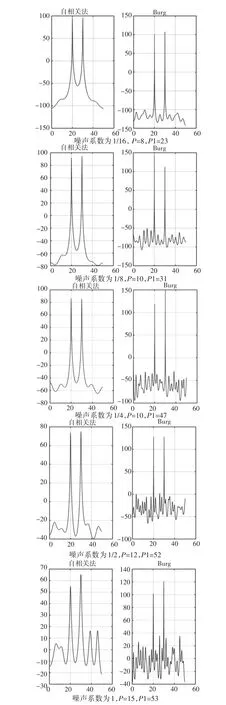
图14 信噪比变化下两种方法的性能比较

图15 最佳阶次随信噪比变化的趋势

4 小信噪比性能分析

本文采用了以下方法进行了仿真：x=sin（2*pi*F1*n）+sin（2*pi*F2*n）+m*randn（size（n））

m为噪声系数，可知，m越大，信噪比越小。采样点数：256，采样频率：100，信号频率：20Hz、30Hz。

4.1 信噪比变化下两种方法的性能

输出阶数P，输出阶数P1（p为自相关法，p1为Burg法）

由此发现，在信噪比逐渐减小的过程中，自相关法的最佳阶次变化不大且缓步上升，而Burg法的最佳阶次却有了明显的增加，并且虚假谱峰现象更加严重，这表明了Burg法在较小的信噪比的情况下性能会下降，而自相关法却没有较为明显的变化。

4.2 相同阶数下改变噪声系数对两种方法的影响

x=sin（2*pi*F1*n）+sin（2*pi*F2*n）+m*randn（size（n）），m为噪声系数，可知，m越大，信噪比越小。采样点数：256，采样频率：100，信号频率：20Hz、30Hz。本次选取一个较大的阶数p=p1=61，改变噪声系数，观测两种方法预测的功率谱，见图16。

由这些图进行比对后发现，相同的阶次情况下，在噪声系数较小时（信噪比较大），Levinson算法分辨率较低，主瓣宽度较大，尖峰处没有Burg法尖锐，尽管Burg法虚假谱峰现象比Levinson法严重，但总体而言，Levinson法性能相较于Burg法较差。

5 结语

本文通过Matlab仿真分析，对比研究了Lenvinson（自相关）算法和Burg算法下的AR模型的谱分辨率，分析了小信噪比情况下的AR模型的性能，主要结论如下：

1）预测阶次较低时，Burg法与Levinson法性能相似，但是随着阶次的提高，Burg法的谱峰比Levinson法更加尖锐，准确度更高，但虚假谱峰现象更加严重。

图16 改变噪声系数，Levinson算法和Burg法预测的功率谱比较

2）在最佳阶次下，Burg算法功率谱的方差较大，而Levinson法的谱线相对平滑。FPE准则对于Burg算法预测的阶次偏高，应稍微降低阶次来减少谱裂，而对Levinson算法来说阶次偏低，应增加阶次来提高分辨率。

3）与Levinson相比，Burg法的预测误差随频差的变化相对较小，预测精度比较稳定。

4）Burg法在较小的信噪比的情况下性能会下降，而自相关法却没有较为明显的变化。

5）相同的阶次情况下，在噪声系数较小时（信噪比较大），Levinson算法分辨率较低，主瓣宽度较大，尖峰处没有Burg法尖锐，尽管Burg法虚假谱峰现象比Levinson法严重，但总体而言，Levinson法性能相较于Burg法较差。