基于多元退化的航空机电系统的剩余寿命预测∗

孟 蕾 许爱强董 超

（1.海军航空工程学院飞行器工程系 烟台 264001）（2.海军航空工程学院飞行器科研部 烟台 264001）（3.海军航空工程学院飞行器基础部 烟台 264001）

1 引言

航空机电系统的状态评估与预测还有剩余寿命的预测对保证飞行安全具有重大意义，愈来愈受到人们的重视。国内外一些先进的理论，如预测与健康管理、基于状态的维修等方法正逐步被采用，这种通过状态监测信息进行寿命预测的方法，是当前理论界关注的热点问题之一。

当前国内外的航空机电系统寿命预测往往着重于从单边退化角度展开论述，是退化量、突发故障单一化的集中体现，退化量的多元化始终未能在学界占主导。针对航空机电系统运行过程中存在的多种退化故障和突发故障并存的竞争故障甚少提及。针对这个问题，本文研究了基于多个退化模式引起的航空机电系统竞争故障问题。首先根据工程经验选取剩余寿命预测所需的监测的有效状态特征参数，基于性能退化故障模式建立了一种改进的新的模型预测性能退化的参数，然后通过建立混合威布尔模型分析退化故障对突发故障产生的影响，在这个基础上预测出突发故障，最后基于多元退化故障和突发故障的竞争故障构建了航空机电系统剩余寿命预测模型，预测了航空机电系统的剩余寿命。立足案例，在比较研究之后，认为本文在方法论上具有优势，满足精度要求。

2 获取监测数据信息

从航空机电系统监测数据中提取大量有效的监测参数进行寿命预测，是当前航空机电系统状态评估与预测的热点问题。航空机电系统的数据主要包括：性能退化数据和突发数据，航空机电系统的性能退化的数据主要来源于状态监测参数，所以性能退化通常反映在监测参数的变化。航空机电系统监测数据具有小样本、维度高的特点，为充分利用这些状态监测参数，需对状态参数进行处理：一是筛选，降低数据利用难度。二是对这些状态监测参数进行融合，本文运用贝叶斯计算工具融合从多个角度全面反映航空机电系统的性能退化情况。突发故障数据信息比较少，一般选取几个经常发生突发故障的主要关键参数。

3 构建航空机电系统的剩余寿命预测框架

为了更有效地对航空机电系统进行剩余寿命预测，首先基于航空机电系统性能退化故障数据和突发故障数据的竞争故障构建了剩余寿命预测框架，如下图1所示。

图1 基于竞争故障的航空机电系统剩余寿命预测框架

4 基于贝叶斯线性模型的航空机电系统性能退化预测模型

假设航空机电系统的性能退化监测参数已知，构建一个航空机电系统监测参数与性能退化程度的关系矩阵 θ ；矩阵表示为：U=(U1，U2，…，vUk)。公式中：k表示个数，Vk是n行列矢量，n表示观测次数。那么航空机电系统性能退化参数与状态监测参数之间的关系，可以用下式表示：

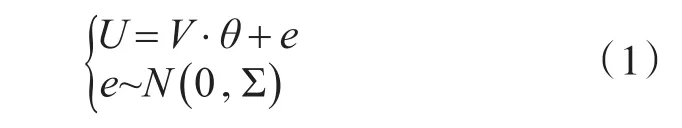
针对航空机电系统的状态监测数据不确定性、随机性的特点，本文采用贝叶斯线性模型处理监测参数，解决了监测数据不确定性的问题，提高了预测精度。根据工程经验，首先假设航空机电系统监测参数服从逆高斯分布［2］，值和协方差可表示为

通过式（2）～（3），可得航空机电系统状态监测数据的期望和方差值；接着计算后验期望，使贝叶斯矩阵Mθ̑最小，表达式为

针对航空机电系统的性能退化数据一般为平稳退化的特点，本文主要采用线性退化模型加以描述航空机电系统各状态特征参数性能退化率［3］。通过航空机电系统状态特征监测参数退化率的变化趋势预测剩余寿命。航空机电系统线性退化率模型可表示为

S(ti)表示ti时刻的累积退化量。ε(ti)可以看作是噪音函数，用来度量ti时刻测量的噪声数据。

根据工程经验，假设航空机电系统监测参数服从正态分布，其均值和方差可表示为μβ和σβ2。通过贝叶斯方法可以不断融合新监测到的参数。假定剩余寿命可表示为TD，性能退化阈值用D表示，则第l个观测点预测剩余寿命为

输入新的监测数据后，代入式（1）可得航空机电系统性能退化程度。估算航空机电系统的退化率之后，采用贝叶斯方法预测航空机电系统未来的退化率。

根据工程经验，假设航空机电系统退化率服从正态分布N(μβ，σβ2)，可证明其先验和后验分布都符合正态分布［3］，其后验期望均值、方差及区间如下式所示：

利用预测的航空机电系统性能退化率期望值，按照S(TD+tl)=D，采用蒙特卡洛仿真方法计算航空机电系统性能退化故障剩余寿命。

5 基于混合威布尔模型的航空机电系统突发故障预测

5.1 混合威布尔模型

针对航空机电系统的不同的多种性能退化故障数据和少量的突发故障数据，我们采用威布尔分布［4］用于航空机电寿命试验的数据处理。当威布尔分布形状参数γ＞1时，就可以得出航空机电系统性能退化与寿命分布变化的关系。针对航空机电系统性能退化有多种不同的性能退化过程，本文采用混合威布尔分布模型描述航空机电系统可靠性［5］。假设航空机电系统由两个威布尔分布组成的，其中一个模型的权重概率为p，那么航空机电系统突发故障的可靠度用式（10）所示

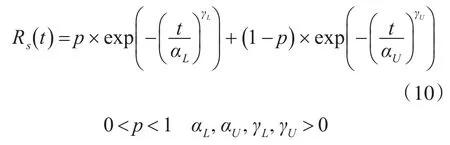
式中，αL，αU为尺度参数；γL，γU为形状参数。

结合航空机电系统的特点，本文对性能退化率的上下限分别建立威布尔模型，航空机电系统可靠度计算如下［6］：

尺度参数α的先验分布：

威布尔分部联合先验分布：

混合威布尔分布联合先验分布：

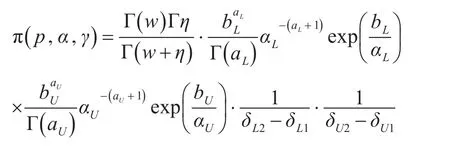
航空机电系统提取的试验数据，针对m次数据，假设k次和第一种威布尔分布吻合，m-k次和第二种威布尔分布吻合，那么构建威布尔分布的似然函数：

分别对 γL，γU和 αL，αU积分，然后采用 Monte-Carlo方 法 仿 真 计 算 ：代入得出对应时刻可靠度。

代入式（11）计算的航空机电系统性能退化率的上下限，采用蒙特卡洛方法［7］分别计算其对应的威布尔分布形状参数，进一步建立混合威布尔分布模型，权重分别为 p和1-p。为计算混合威布尔分布中各参数的期望值，需要计算先验分布逆Ga(a，b)、Beta(w，η)的超参数［8］。

5.2 逆Ga(a，b)超参数先验和后验参数学习

已知参数α的均值和方差，尺度参数可表示为

则超参数a和b可得：

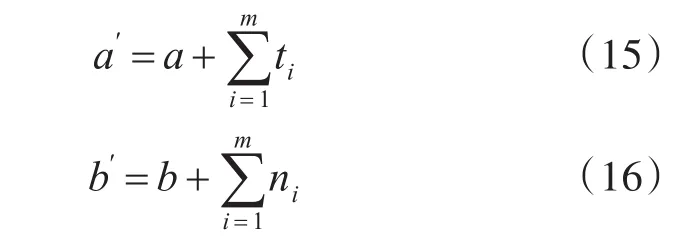
5.3 Beta(w，η)超参数先验和后验参数学习

分布参数的先验分布为 π(p)=B(p ，w，η )，一般假设p0=0.5，先验信息和超参数的关系为

先验分布、后验分布超参数之间的关系可表示为

6 基于退化数据和故障数据的航空机电系统的剩余寿命预测

将第5节求得参数代入图1和式（10），得到航空机电系统突发可靠度，然后采用蒙特卡洛方法计算 剩 余 寿 命。 航 空 机 电 系 统 剩 余 寿 命，取剩余寿命较小值是出于风险控制的考虑。

7 实例分析

我们选取航空机电系统中最典型的复杂系统航空发动机为例，根据发动机系统主要的状态监测参数，依据监测时刻起的飞行时间，以提取的10个监测点作为样本，假设其复合伽马随机过程，采用蒙特卡洛仿真方法计算得到航空发动机的性能退化程度。

表1可得10个监测点可求得各监测参数之间的关系。利用4.1的算法，融合各性能监测参数后的性能退化值与实际退化值误差极低。利用（5）可得性能退化率，利用（15）、（16）更新不同时刻的性能退化率，代入式（6）预测航空发动机系统性能退化剩余寿命。代入式（17）计算退化率的上下限，构建混合威布尔分布。

表1 某机电系统采集到的性能监测参数

根据表1给出的某发动机进行的3次检测与维修，可确定突发故障的先验值为E(R3000)=0.97，σ2(R3000)=3.76×10-4，p0=0.5，代入式（19）计算相关超参数。根据式（10），采用蒙特卡洛方法，预测航空发动机系统突发故障寿命。

表2 某航空发动机系统采集到的监测参数的预测

本文实验分别对以上3个监测点预测航空发动机系统寿命，以R=0.90作为可靠度阈值，该发动机系统的性能退化故障剩余寿命TD、突发故障剩余寿命TS，取两者的最小值，计算结果如表2所示。某航空系统发动机系统实际剩余寿命是在第3次监测后，求得实际可靠运行2187飞行小时，预测结果整体误差率低于5%。为说明本文方法的有效性，选择了两种不同方法进行对比，对比结果如表3所示。

表3 不同方法的对比结果

通过对比分析可得，第二种方法误差虽小，但风险大。第三种方法风险小，但是误差大。因此，本文方法兼顾了误差和风险，优于这两种方法。

8 结语

针对性能退化故障和突发故障同时并存的情况建立航空机电系统剩余寿命预测模型，该方法能充分利用状态监测数据，分析性能退化故障与突发故障的相关度，准确地描述航空机电系统寿命变化趋势，提高了航空机电系统剩余寿命预测的准确度，并为航空机电系统复杂装备的理论支撑奠定了基础。