基于TDOA的自适应扩展卡尔曼滤波跟踪算法研究∗
2018-08-01周恭谦杨露菁
周恭谦 杨露菁 刘 忠
(海军工程大学电子工程学院 武汉 430033)
1 引言
UWB无线定位技术是目前定位领域研究的热点之一,无论是在军事领域还是商业领域都有广泛的应用价值。高精度、低功耗的特点使UWB无线定位技术成为未来定位技术的首选。UWB脉冲由于具有极高的带宽,持续时间短至ns级,因而具有很强的时间分辨能力[1]。为了充分利用UWB时间分辨能力强这个特点,使用基于信号到达时间估计(TOA)的测距技术是最适合于以UWB无线定位的。UWB脉冲的TOA估计算法近几年得到了较为充分的研究,包括采用高采样速率、高精度的匹配滤波技术(Match Filter,MF)来实现的基于相干检测的TOA 估计算法[2~4],以及采用较低采样率、降低了复杂度的基于非相干能量检测的TOA估计算法[5~8]。在国外,UWB 定位上的研究主要有:Win和Scholtz提出多径UWB环境下的最大似然(ML)检测方法[9];Cramer等基于CLEAN算法提出了一种包 含 TOA、AOA 参 数 的 UWB 信 道 模 型[10];Joon-Yong Lee等提出了在UWB无线链路上基于TOA的范围测量方法[2]。而TOA方法是利用信号的传播时延进行测距,由于UWB信号具有良好的时间分辨率,信道环境的变化对信号的传播时间也没有影响,因此基于时间的定位具有相对较高的精度。但目标节点和基站之间时钟的严格同步存在困难,如果不完全同步将造成很大的定位误差。TDOA在实际中实现该技术的可能性与TOA相比要高的多,这是因为它不要求基站与待测目标之间时钟同步,只需要每个基站之间时钟同步就能得到TDOA值,并且在对到达时间做差的过程中会减小部分误差,定位精度能相对提高。而针对TDOA动态目标跟踪定位问题张丽[11]提出了一种基于TDOA定位的扩展卡尔曼滤波算法(EKF)并将其应用到UWB系统中,通过仿真结果和Taylor算法,Chan式算法对比表明该算法能够降低定位误差,实现良好的跟踪定位,但该算法当TDOA测量误差较大时定位精度降低而且容易发散,针对这种情况,本文提出了一种自适应迭代扩展卡尔曼滤波算法(AIEKF),并通过仿真对比证明了该算法在测距误差增大时,仍能保持良好的定位精度和收敛速度。
2 基于UWB的TDOA跟踪算法研究
在无线定位中,一旦取得TDOA测量值,就可以得到待测目标到两个定位基站之间的距离差,多个TDOA测量值就可以构成一组关于待测目标位置的双曲线方程组,求解该双曲线方程组就可得到待测目标的估计位置。设(x,y)为待测目标的待估计位置,(xi,yi)为第i个定位基站的已知位置,则待测目标和第i个定位基站之间的距离ri可以表示为

对式(1)求解即可得到待测节点坐标(x,y)。
2.1 基于TDOA定位的扩展卡尔曼滤波算法
卡尔曼滤波算法适用于解决噪声为高斯噪声的线性问题,但由于实际中经常会碰到非线性问题,因此研究者对卡尔曼滤波算法进行改进,将卡尔曼滤波方法推广到非线性问题,提出了处理非线性问题的扩展卡尔曼滤波(EKF)算法。非线性系统的状态方程和观测方程分别为[12]

对于TDOA二维定位,设参与定位的基站数为M(M ≥3),可以得到M-1个TDOA数据,系统的状态方程是线性的,观测方程是非线性的,系统的观测方程如式(4)所示。

ri为待测目标和第i个定位基站之间的距离其表达式可见式(1),vi1表示观测噪声。
对应观测方程Y=h(X)+V的矩阵形式的各个参数可表示为

移动待测目标的状态方程如式(5)所示

其中Sk=[xk, yk, vxk, vyk]T是tk时刻的状态向量,(xk,yk)是目标节点在tk时刻的二维坐标信息,vxk,vyk分别代表目标节点在x方向和y方向的分速度。

噪声向量Wˉk-1的协方差矩阵为Qk-1,状态转移矩阵为φ',它们的定义如下:
其对应的观测过程如式(7)所示

其中Zk是测量数据向量,h(Sk)为非线性变换,Vˉk是测量噪声,则协方差矩阵R'可表示为

其中
由于h(Sk)是非线性变换,对h(Sk)利用高等数学中的Taylor级数展开,为k时刻 h(Sk)在处的Jacoby矩阵。
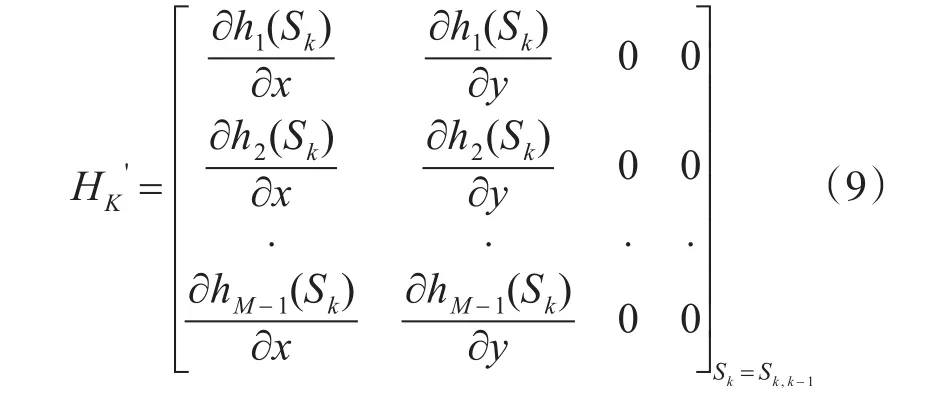
扩展卡尔曼滤波的运算与卡尔曼滤波方法相似,同样由两个递归过程完成。
不同的是,在扩展卡尔曼滤波过程中函数h(Sk)需要进行线性近似,通过非线性函数的局部线性化特性来近似描述其非线性。扩展卡尔曼的算法过程如下:

2.2 自适应迭代扩展卡尔曼滤波
EKF系统中,测量误差增大时Vk=h(Sk)-Zk会增大,而增益矩阵因离线计算的原因,未能根据实时的状态在线调整增益矩阵,仍将趋于极小值,不会随测量误差Vk的增大而变大,导致EKF滤波精度下降,甚至发散。传统传统FEKF[13]在式(21)中引入 λk
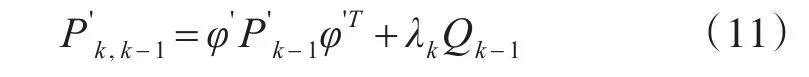

欲使状态估计值接近于真实值此时满足[14]:
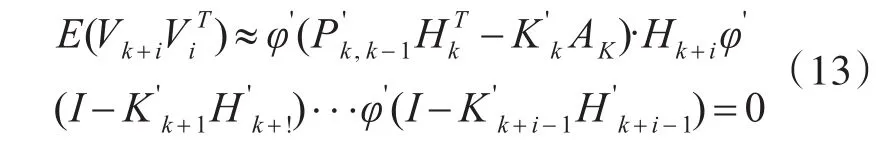
其中AK表示误差方差矩阵,此时
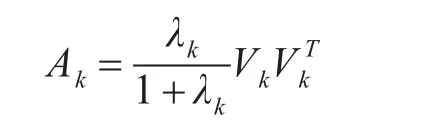
欲使式(14)右边满足等式则有

将式(10)代入式(14)化简可得:
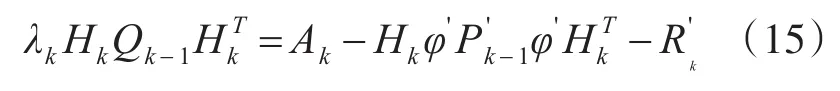
对式(15)求解 λk可得

当 λk<1时,系统噪声不进行迭代,而当 λk≥1时,系统噪声进行迭代,此时随着λk增大系统噪声增大,能够实时调整增益矩阵,从而提高测量精度。
2.3 仿真实验
假设目标作匀速直线运动,初始位置坐标为(1000m,1000m),航向角 KW=π/4,速度 vx=10m/s,vy=10m/s。采用3个基站,其坐标依次为(0,0),(2400,0),(0,2200),采样时间为0.1s,信道采用IEEE802.15.4a标准中的室内居住环境CM1(LOS)信道。
当测距误差服从均值为0,均方差为1m的高斯白噪声,其跟踪曲线和速度估计如图1、2。当测距误差服从均值为0,均方差为100m的高斯白噪声,其跟踪曲线和速度估计如图3、4所示。其算法性能比较如图8所示,其中均方根误差RMSE(Root-Mean-Square error)可由式(17)计算:

从图1和图3对比可知当测距误差改变时自适应迭代卡尔曼滤波定位精度明显上升,这是因为当测量误差增大时,渐消因子也随之改变从而系统噪声也随之变化,最后导致增益矩阵的改变,定位精度随之提高,图2和图4对比显示出在对目标跟踪定位上自适应迭代卡尔曼滤波具有更高的定位精度,这也是和渐消因子的引入相关的。从图5对比两种算法的RMSE可以看出,自适应迭代滤波在保持高定位精度的同时能够更快速的收敛,从而验证了其比扩展卡尔曼滤波具有更高的定位精度和更快的收敛性。

图1 测距误差较小时跟踪曲线
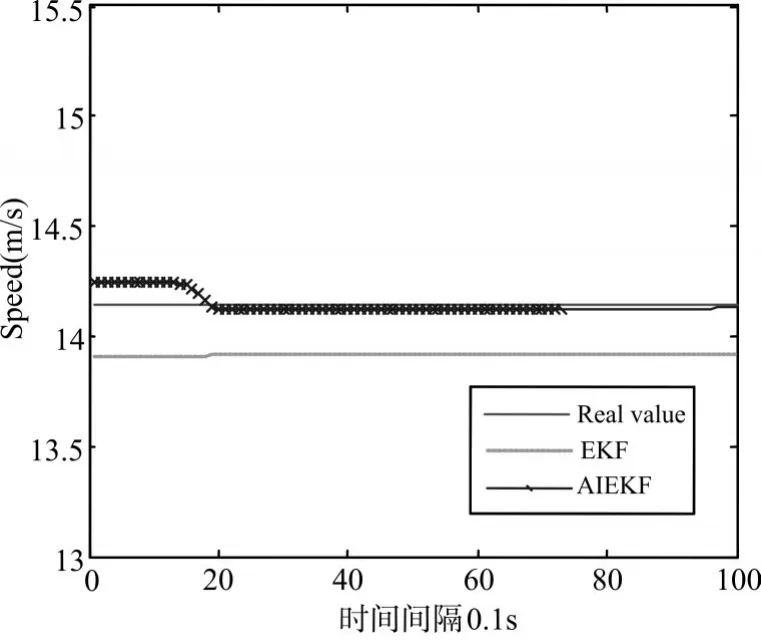
图2 测距误差较小时目标速度估计
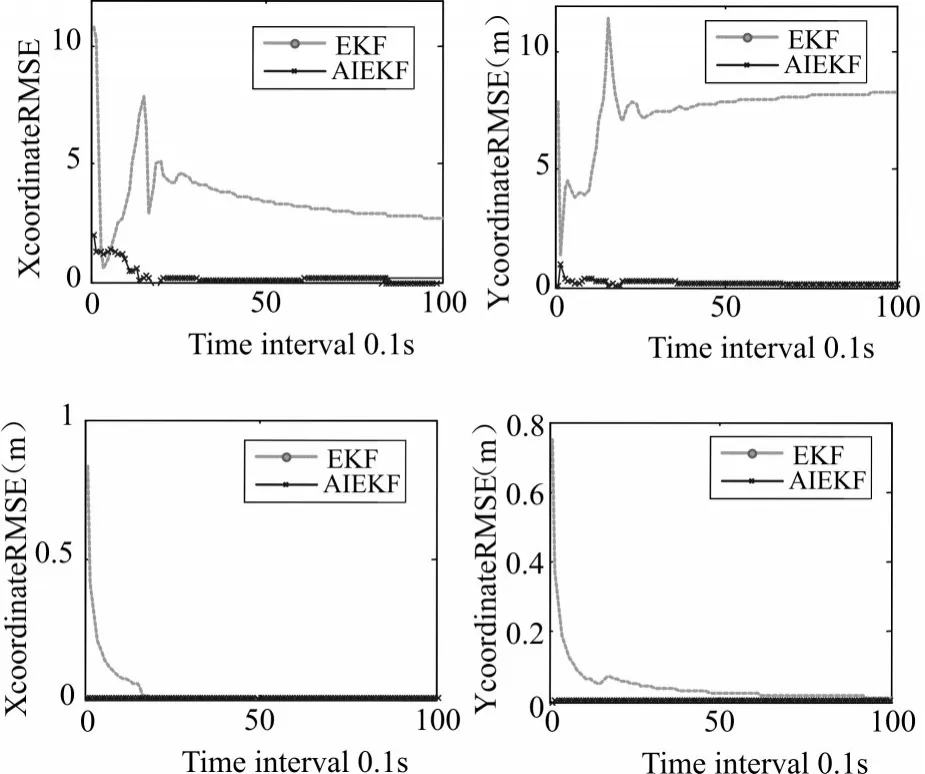
图3 测距误差较大时跟踪曲线

图5 测距误差较大时EKF与AIEKF算法性能比较

图4 测距误差较大时目标速度估计
3 结语
本文对UWB中基于卡尔曼滤波的TDOA跟踪定位算法研究。针对EKF算法会随着测量误差增大定位精度降低这一缺点,提出了一种自适应迭代扩展卡尔曼滤波算法(AIEKF),通过仿真对比表明该算法在测距误差增大时,该算法能保持良好的定位精度和收敛速度。
