基于GA优化BP神经网络小电流接地系统故障选线方法

薛太林， 侯隽朗， 张建新

(山西大学，山西 太原 030013)

0 引 言

在我国，10 kV～35 kV配电网一般采用小电流接地系统，随着电网结构的复杂与馈线数量的增加，此类配电网发生单相接地故障的几率非常大，而小电流接地系统单相接地故障选线问题一直是工程实际和现场运行中的难点[1]。目前，较为成熟故障选线方法可分为外加信号法[2-3]与故障信号法[4-5]，故障信号法又可分为故障稳态信号法[6-7]与故障暂态信号[8-10]。但是，只基于单一判据的选线方法往往会出现选线误判，所以基于多种判据融合的选线方法是解决误判的有效途径[11]56。

文献[11]60提出了一种基于综合评判的多判据融合选线方法，但只构造了单一判据的隶属度函数，进行综合评判时各判据的权重系数是固定的，对各种复杂故障情况的适应性较差。文献[12]提出了基于蚁群算法的神经网络故障选线方法，该方法加入了BP神经网络，对多种故障情况有一定的适应性，但面对实际复杂故障情况可能会出现两个判断结果,导致选线失败。文献[13]提出了应用遗传算法(GA)优化学习量量化(LVQ)神经网络的配电网单相接地故障选线方法，利用了LVQ网络的分类功能，将故障选线问题看成一类特殊的分类问题，但该方法只判断了故障线路与非故障线路暂态特征量的差别，没有做到多判据融合的判断，无法适应各种复杂故障情况。文献[14]提出基于量子神经网络和证据融合的小电流接地选线方法，也达到多判据融合选线的目的，但其网络结构复杂庞大，对权值阈值的整定较为复杂。

针对以上问题，本文提出基于遗传算法GA(Genetic Algorithm)[15-16]优化BP(Back Propagation)神经网络选线方法，利用BP神经网络自身的泛化能力，达到多判据融合的目的，提高了对复杂故障情况的适应性，同时加入遗传算法，克服了BP神经网络对初始权值阈值的敏感，提高网络的精度与收敛速度，有效地解决了选线方法存在的问题，提高了选线的精度与速度。

1 基于GA优化BP神经网络模型

1.1 BP神经网络

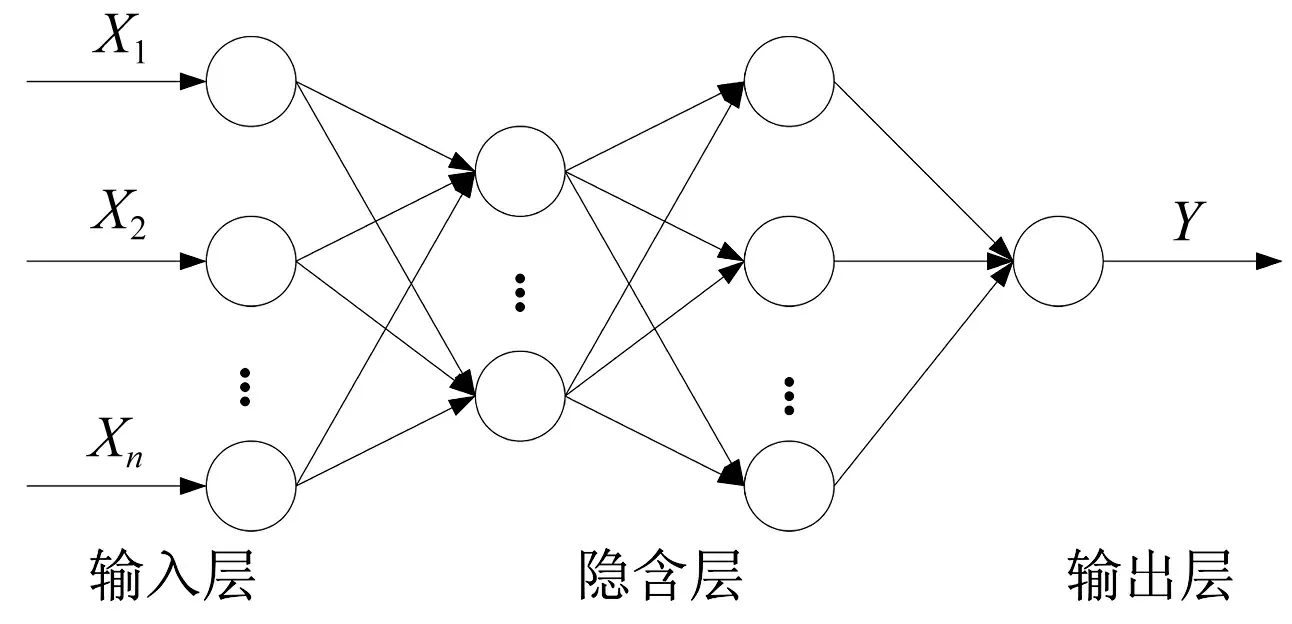
图1 神经网络模型

BP神经网络，即反向传播神经网络，这种传统的多层前馈神经网络，包含输入层、隐含层和输出层(如图1所示)，是当前在各个领域都有很多运用人工神经网络模型之一。

1.2 GA-BP神经网络

遗传算法(Genetic Algorithm)是通过迭代计算寻找相应问题最适应解集的算法，具有全局搜索，不受每次迭代的梯度值的影响，不会陷入局部死区等优点。使用遗传算法对BP神经网络的初始权值阈值进行优化，可提高网络的精度与收敛速度。

图2 GA优化神经网络流程图

遗传算法对神经网络初始值进行优化的基本步骤(流程如图2所示)：

(1)编码：本文对网络初始值进行二进制编码。确定网络拓扑结构，输入层神经元有n个，隐含层神经元有s个，输出层神经元有m个，则需要编码的初始值个数为：

N=n×s+s×m+s+m

(1)

(2)初始种群：经过编码后的N个网络初始值数据即构成了初始种群。

(3)适应度评估：适应度为个体与最适应解集的相似程度，BP神经网络的误差一般选取各层实际输出与期望输出的平方作判定，本文针对遗传算法的特点将适应度函数定义为各层平方误差的倒数：

(2)

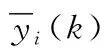
(4)选择：运用比例选择算子，结合轮盘赌法，进行选择操作。

(3)

式中：Fiti为第i个个体的适应度；Pi为第i个个体被选中的概率。

(5)交叉：交叉运算指交换不同个体对应部分的数据。本文采用单点交叉运算，交叉概率Pc取0.2。

(6)变异：变异指设置变异概率选择某一个体，将此个体进行修改。GA中对变异概率的取值一般都很小，本文变异概率Pm取0.05。

(7)产生新种群，判断是否满足迭代终止条件，对最终种群进行解码即可得到网络初始值的优化值。终止代数T是指GA完成整个运行过程所需总的迭代次数。本文终止代数T取100。

最终，即可得到GA-BP神经网络模型。

2 基于GA优化BP神经网络故障选线原理

2.1 选线原理

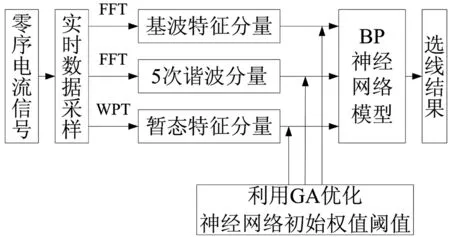
图3 故障选线原理框图

为实现故障选线的多判据融合，分析故障零序电流提取故障特征分量，采用快速傅里叶变换(FFT，Fast Fourier Transform)算法提取零序电流稳态特征分量，包括基波、5次谐波特征分量；小波包变换(WPT，Wavelet Packet Transform)算法提取零序电流的暂态特征分量。将各个特征分量输入训练完成的GA-BP神经网络模型，即可输出选线结果,如图3所示。

2.2 零序电流故障特征提取

(1)基波幅值特征分量提取。在小电流接地系统中，当中性点不接地，发生单相接地短路故障时，流过故障线路的零序电流比流过其他各条线路的电流幅值都要大。因此，可通过比较零序电流基波幅值的大小来确定故障线路。

基波幅值特征分量定义如下：

(4)

式中:I1k为第k条线路的零序电流基波幅值;I1Σ为所有线路的零序电流基波幅值之和。

(2)5次谐波特征分量提取。在经消弧线圈接地的小电流接地系统当中，由于消弧线圈值针对零序电流基波的电容电流进行补偿，各次谐波中5次谐波的特征最为明显，可利用5次谐波特征分量来选择故障线路。

5次谐波特征分量定义如下：

(5)

式中:S5k为第k条线路零序电流5次谐波分量的视在功率;S5Σ为所有线路零序电流5次谐波分量的视在功率之和。

(3)暂态特征分量提取。对暂态故障信号进行处理时，传统的时域分析与频域分析都无法准确提取其暂态特征，需要运用信号的时频分析法——小波包分析，可以很好地对信号的高频部分进行分解并作分析。小电流接地系统发生单相接地故障时，暂态信号的频率很高，其幅值和能量可达稳态信号的数倍，选用小波包变换的小波基为db2小波，将流经各条线路的零序电流按最适应的频带宽度进行分解，为了使信号的高频暂态特征更加明显，应剔除工频基波所在的频带，其余高频能量集中频带的总能量定义如下：

(6)

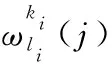
暂态特征定义如下：

(7)

式中:εk为第k条线路零序电流的暂态能量;εΣ为所有线路零序电流的暂态能量之和。

2.3 GA-BP神经网络结构

GA-BP神经网络模型设置为含有两个隐含层的四层前馈神经网络(如图1所示)，网络的输入为零序电流的故障特征分量X1、X2、X3，三个输入节点，根据经验，第一隐含层设置8个节点，第二隐含层设置3个节点，输出层有1个节点，形成3-8-3-1型结构的GA-BP神经网络。最终，定义误差范围，判断网络输出与1的接近程度来判别该线路是否为故障线路。定义网络输出误差为：

δ=|output-1|×100%

(8)

式中:output为神经网络的输出值。当网络输出误差δ超出所定义的误差范围，则该条线路即为故障线路，反之为正常线路。

3 仿真分析

3.1 仿真模型的建立

图4 仿真模型

神经网络的训练需要大量的数据作为支持，经过训练的神经网络模型在输入相关参数后才能获得有意义的选线结果。本文在MATLAB/Simulink中搭建小电流接地系统仿真模型，其中电源选择三相电源，线路采用π型等效线路，负载采用相同的三相负载，仿真模型如图4所示，模型参数见表1[17]。进行仿真分析时，运用MATLAB/Simulink中的Powergui模块，选择离散算法(discrete模式)，设置采样时间为1×10-5s。

表1 仿真模型参数表

3.2 训练集与测试集的生成

在MATLAB/Simulink搭建的模型中，通过设置不同的故障线路、故障位置、故障初始角、故障点过渡电阻以及电源中性点接地方式与消弧线圈补偿度，运用排列组合的方式，就可以得到若干组不同的故障零序电流波形。其中，根据采样定律，将模型中零序电流的采样频率设置为3 kHz，并取故障前一个周波和故障后一个周波的电流信号，对每个电流信号运用FFT和WPT算法，计算每个零序电流信号的故障分量，得到若干组故障特征分量作为训练样本输入，即可输出该线路是否故障。其中，利用FFT算法，根据式(4)、式(5)，可以分别提取到故障零序电流的基波幅值特征分量和5次谐波特征分量；利用db2小波包对故障零序电流进行4层小波包分解，得到剔除工频所在频带的小波包分解系数，根据式(6)、式(7)，可以提取到故障零序电流的暂态特征分量。

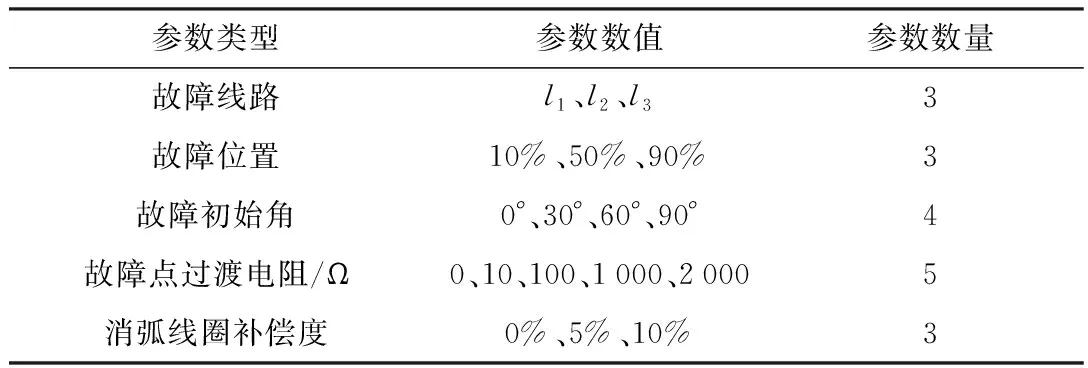
表2 训练样本参数设置

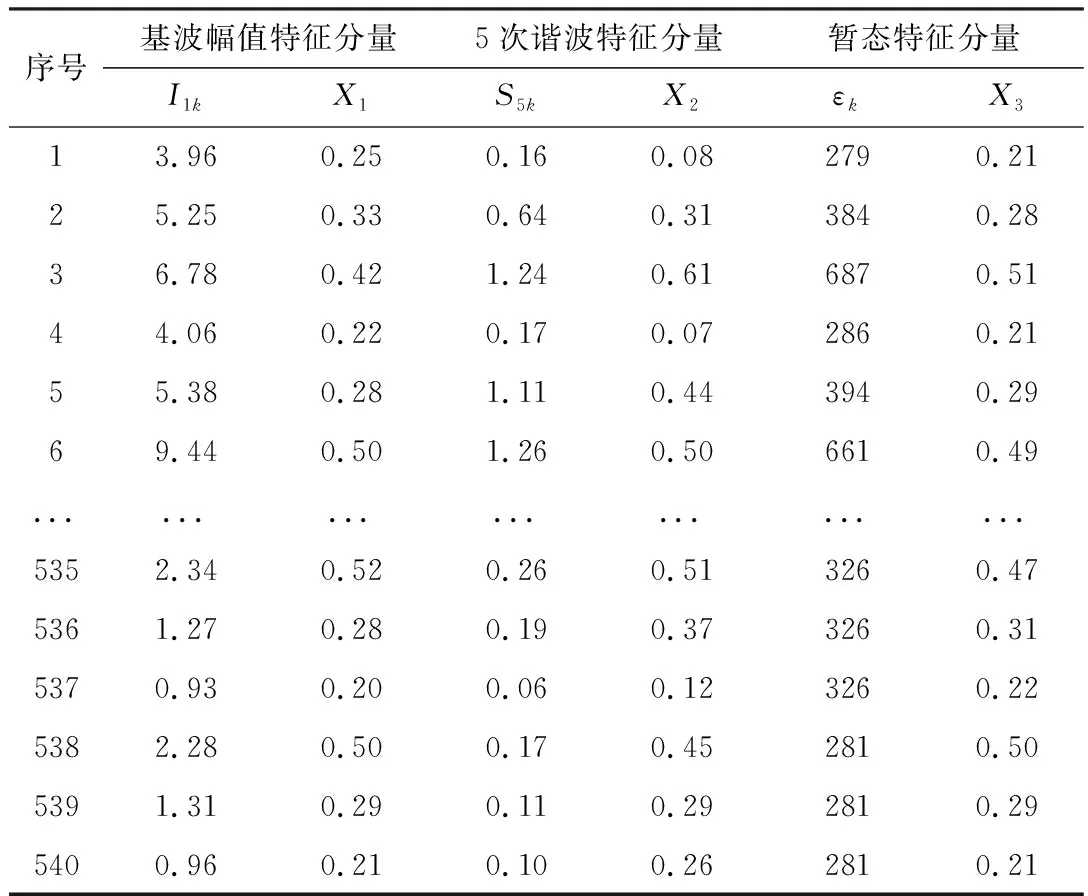
表3 原始数据

3.3 仿真测试结果与分析

本文对GA-BP神经网络与传统BP神经网络训练时的迭代收敛速度进行对比，分别输入训练集490组数据，两种网络的收敛速度如图5所示。从图中可知，网络迭代终止的条件是期望均方误差为0.1，GA-BP神经网络仅需经过5次迭代即可达到稳定，而传统BP神经网络需要经过12次迭代方能达到迭代终止条件。由此可见，经遗传算法优化网络初始值可使网络迅速收敛，大大缩短了网络训练的时间。将这种优化方法运用到现场实际当中处理更加庞大的数据时就具有更加明显的现实意义。

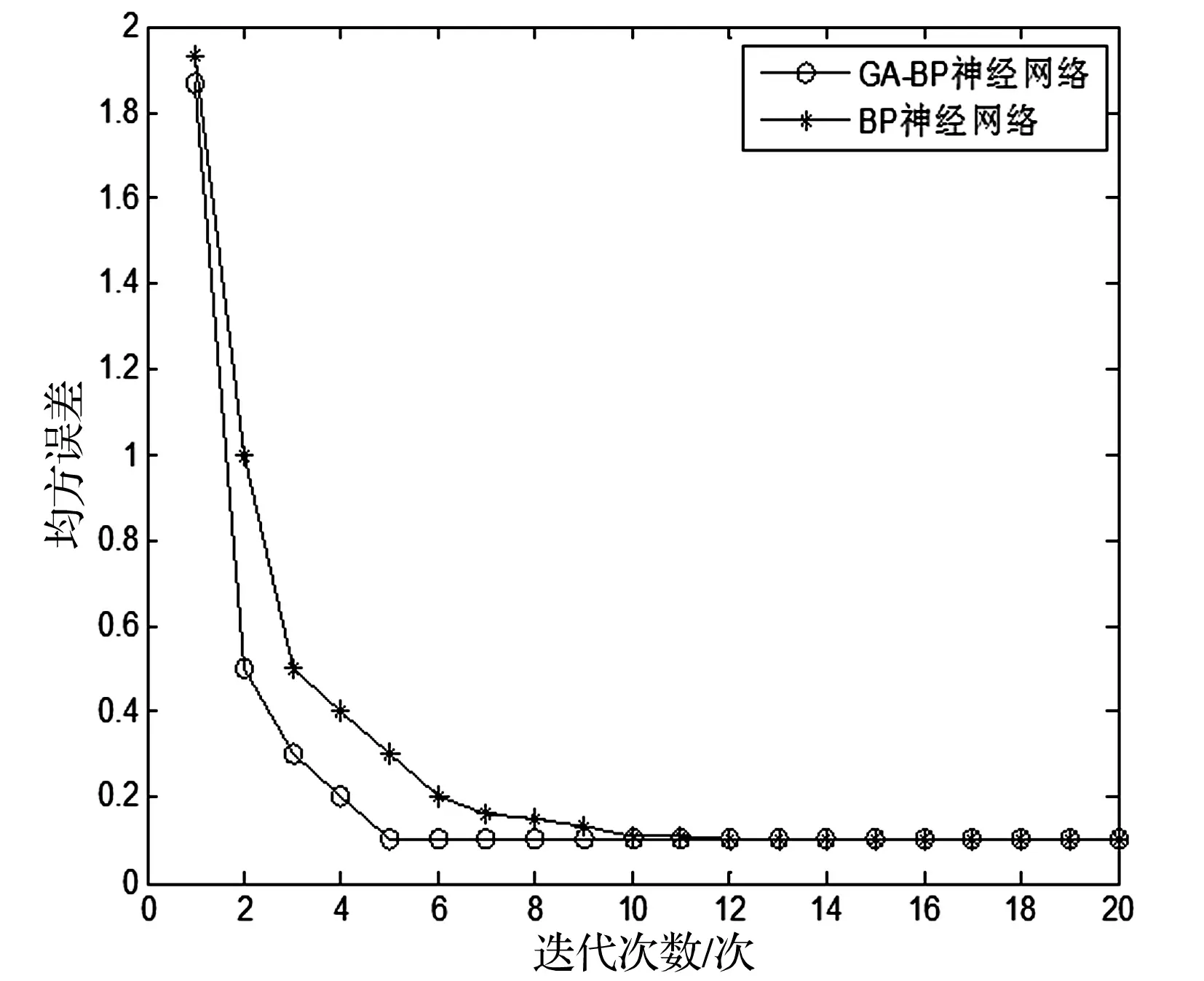
图5 网络收敛速度对比

对比GA-BP神经网络与BP神经网络选线的测试结果，分别输入测试集50组数据，两种网络的输出如表4所示。

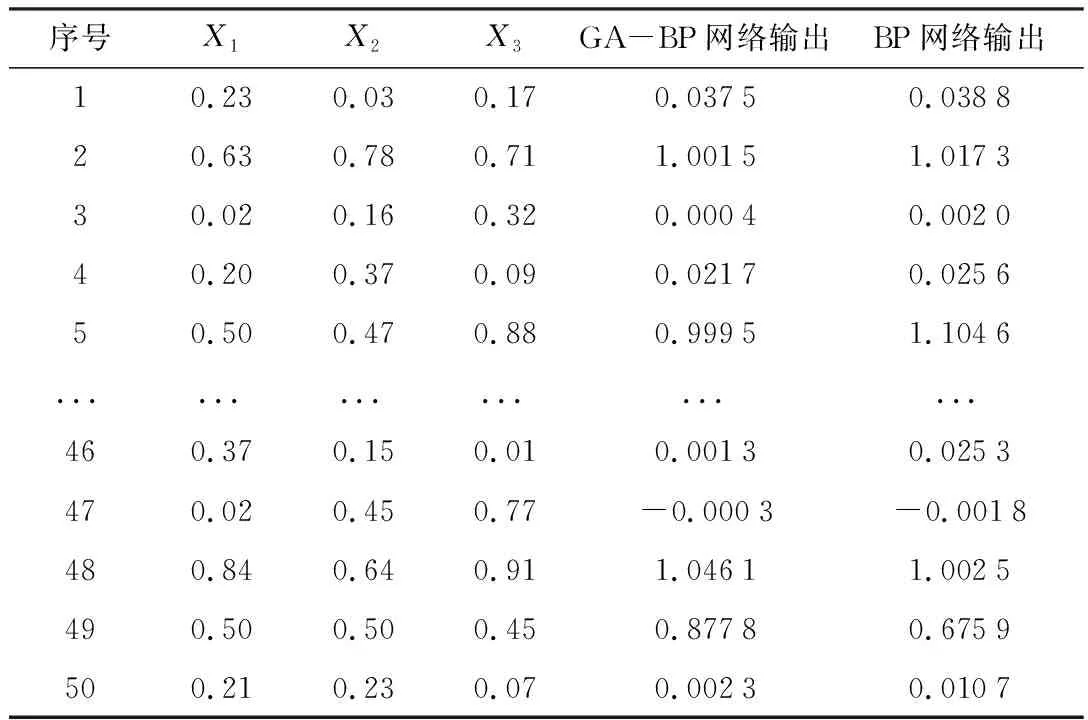
表4 测试集故障分量与模型输出

经过数据分析，比较网络输出值与1的接近程度，设置网络输出误差δ大于1%即为误判，根据式(8)计算误差δ，经统计，传统BP网络在处理第5、16、23、25、35、37、43、44、49组数据时发生了误判，判断精度为82%，而GA-BP网络在第9、13、49组发生误判，判断精度为94%，可看出GA-BP神经网络的判断精度显著提高。

4 结束语

本文针对小电流接地系统故障选线运用单一判据易产生误判，引入BP神经网络进行多判据融合；针对BP神经网络对网络初始值的敏感，运用遗传算法对网络初始值进行优化，过程中针对BP神经网络的特点，着重对算法适应度函数进行选择，交叉、变异概率等参数进行整定，提出基于遗传算法优化BP神经网络选线方法。提取零序电流的三个故障分量，构成网络的输入，运用遗传算法对网络初始权值进行优化，然后对网络进行训练，构成故障选线模型。仿真结果表明，遗传算法可大大提高神经网络的收敛速度，且GA-BP神经网络判断精度高，不受故障位置、故障初始角、过渡电阻及消弧线圈补偿度等因素的影响，具有较高的可靠性。