双端柔直输电系统的改进无差拍控制策略研究
2018-07-31张汀荃张汀荟张海龙顾佳易
张汀荃, 张汀荟, 张海龙,顾佳易
( 1. 南京师范大学南瑞电气与自动化学院, 江苏 南京 210042;2. 南京工程学院电力工程学院, 江苏 南京 211167)
0 引言
随着环境污染的日益加重,风能、太阳能等分布式能源以环保、可再生、运行灵活等优点成为研究的热点,然而其缺点也非常突出,比如存在间歇性功率波动、远离用电中心、规模小比较分散。另外,我国人口在不断增长,城市用电量在不断上升,城区供电网络的改造扩容也变得日益重要[1-2]。柔性直流输电技术(voltage source converter-high voltage direct current, VSC-HVDC)的出现很好地解决了上述难题。VSC-HVDC被大规模运用于实际工程,主要由电压源型换流器(voltage source converter, VSC)、PWM调制技术等为基础组成,在分布式能源并网、无源网络供电和城区供电改造等场合拥有不可替代的优势[3-5]。
本文以两端柔直输电系统为研究对象,建立两端柔直数学模型,研究系统基本运行方式以及VSC控制策略。考虑传统无差拍控制运用于VSC换流器时具有控制延时以及电流闭环控制响应性差等问题,因此提出一种改进无差拍控制策略,通过预测k+2时刻采样电流,解决上述缺陷。最后通过联合仿真,验证所提方法的正确性与可靠性。
1 两端柔直数学模型
如图1所示,两端柔直由换流站1、直流侧电容、换流站2依次连接构成,直流侧电容为系统提供稳定直流电压,保证有功、无功潮流流动,电抗器XLi用以滤除整流端和逆变端输入、输出电流谐波。本文对系统进行分析时,为便于数学模型推导,忽略换流器并联损耗,换流器串联及其他损耗用等效电阻Ri表示[12-16]。
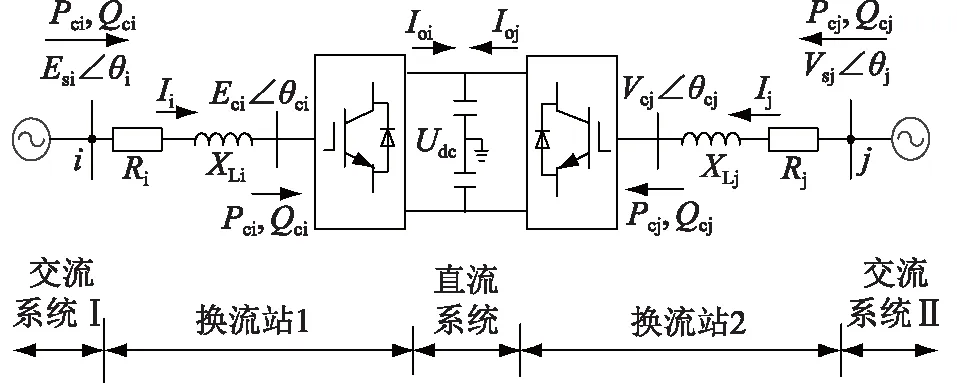
图1 两端柔直主电路结构Fig.1 VSC-HVDC main circuit structure
1.1 三相坐标系下两端柔直数学模型
根据图1,对柔性背靠背直流输电系统列KCL方程,可得其在三相静止坐标系下的动态微分方程:
(1)
式中:ij1,ij2分别为交流系统输入、输出电流;Esj,Vsj分别为交流系统输入、输出电压;Ej,Vj分别为换流器1、换流器2交流侧输入、输出电压。
由于换流器1和换流器2结构参数对称,故只对换流器1三相桥臂开关函数进行定义:
(2)
将式(2)代入式(1)得:
当今时代,计算机软件发展的主流趋势就是智能化,实现计算机软件的智能化有助于对计算机的进一步应用和开发。人工智能技术在各个领域的应用越来越成熟,也越来越广泛,对于相关计算机产品的需求也越来越智能化,这就使得计算机软件相关开发过程在未来也会朝着智能化的方向发展,这也是未来软件开发相关人员的工作重点和课题攻关的方向。
(3)
图1可得直流侧电压方程为:
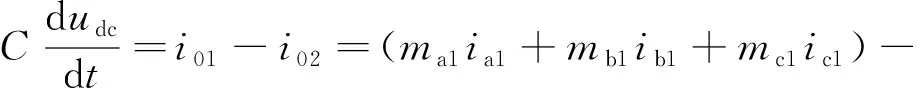
(4)
式中:udc为直流侧电压;i01,i02为直流侧输入或输出电流。假设忽略换流器开关损耗,可得:
(5)
式中:Pc1,Pc2分别为换流器1、换流器2交流输出或输入有功功率。当直流侧udc保持恒定时,系统处于稳定运行状态,i01=i02,则Pc1=Pc2,即流入功率等于流出功率。可得结论:要实现柔性背靠背两侧功率的平衡,需保证直流侧电压的稳定。
式(3)构成了两端柔直系统数学模型,式(4)构成了直流侧电压的数学模型,式(3)与式(4)构成两端柔直系统在三相静止坐标系下的数学模型。
由于三相静止坐标系下参数均为变交流量,不利于系统控制与设计,所以需将两端柔直数学模型转化到同步旋转的dq坐标系下,将三相静止坐标系下的正弦变量转化为同步坐标下的直流量。
1.2 dq坐标系下两端柔直数学模型
根据式(3)、(4)建立两端柔直在dq同步旋转坐标系下的数学模型:
(6)
(7)
直流侧电压在dq旋转坐标下的方程为:
(8)
式中:ω1,ω2为交流系统相电压的角频率;id1,id2,iq1,iq2为交流系统三相交流电流在dq轴上的分量;Esd,Vsd为两端交流系统三相电压在d轴上的分量;md1,md2,mq1,mq2为换流器开关函数在dq轴上的分量。式(6—8)共同构成两端柔直系统在dq旋转坐标系下的数学模型。
2 基于改进无差拍系统运行分析
2.1 传统无差拍控制策略
无差拍控制综合了系统状态方程、系统输出反馈方程以及所要求的下一时刻参考输出方程最终计算出系统所需的开关脉冲。与其他VSC控制策略相比,具有开关频率固定、动态响应快和高带宽特性等优点,在实际中得到了广泛的应用[17]。
在数字系统中,为实现无差拍的控制效果,需将系统下一时刻参考输出量表示为系统状态变量与输出反馈变量之间的相互关系。根据式(6)、(7),由于αβ轴上方程对称,仅以α轴为例,可得α轴无差拍控制框图,见图2。图中Gpwm(z)是PWM调制环节传递函数,Gp(z)是被控对象传递函数。

图2 α轴无差拍电流控制框图Fig.2 Block diagram of current loop with deadbead control
由图2可知,传统无差拍电流控制实际上已经成为了差一拍控制,无法实现无静差跟踪。且受限于系统硬件及控制器容量,系统采样率不能过高。同时考虑系统运用环境,需要更高的控制精度及响应速率。因此,传统无差拍控制已不能满足实际工程应用要求,需进行改进,提高控制效果[18]。
2.2 改进无差拍控制策略
由于实际控制器存在采样率、计算能力等限制,传统无差拍无法实现采样、计算、占空比输出在同一时刻完成,总会存在采样点超前占空比输出点的情况。图3是控制延时示意图,图中在第k时刻开始,系统仍执行的是k-1时刻PWM占空比Dk-1,而上一时刻的占空比Dk延时td才输出。为进一步提高无差拍控制精度,修正由以上原因造成的周期性偏差,改进算法通过预测第k+2时刻的电流,这样PWM占空比Dk+1可以在第k+1时刻提前执行,实现电流无静差跟踪。由于αβ轴上方程是对称的,仅以α轴为例,可得α轴改进无差拍控制框图,如图4所示,其中S为补偿器,用于被控对象相位补偿。

图3 控制延时示意图Fig.3 Sketch map of control delay

图4 α轴改进无差拍控制框图Fig.4 Block diagram of current loop with improvement deadbead control
由式(6)、(7)推算下一时刻电流值,忽略系统电容的影响,默认电流iik1=isk1=i,则第k+2时刻的α轴电流采样值为:

(9)
根据式(6)、(7)及式(9)可得第k时刻和第k+1时刻α轴的电流偏差值:
(10)
(11)
令第k+1时刻α轴的电流误差等价于2个相邻时刻电流误差的平均值,表达式为:
(12)
将式(12)代入式(11),可得系统交流侧输出电压表达式:
(13)
相对于电网基频而言,如果采样周期较小,可以认为在α轴上网侧电压在连续3个采样时刻采样偏差相等,表达式为:
Ugα(k+1)-Ugα(k)=Ugα(k)-Ugα(k-1)
(14)
由式(14)可知,在第k+1时刻的电网电压平均值可由前几个采样值的线性外推得到,表达式为:
Ugα(k+1)=Ugα(k)+[Ugα(k+1)-Ugα(k)]=
2Ugα(k)-Ugα(k-1)
(15)
假如网侧电压在连续4个采样时刻采样间隔也相等,即:
Ugα(k+2)-Ugα(k+1)=Ugα(k+1)-Ugα(k)=
Ugα(k)-Ugα(k-1)
(16)
由式(15)、(16)可得第k+1时刻网侧电压为:
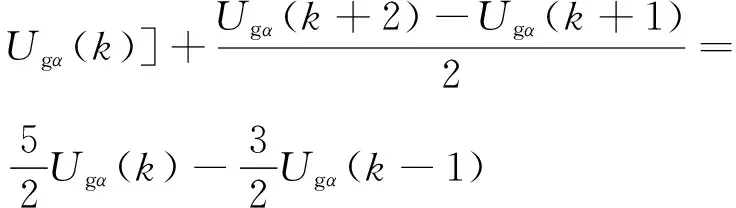
(17)
式(13)中第k+2时刻采样电流为k采样时刻的给定值,表达式为:
iα(k+2)=i*
(18)
根据以上分析,利用式(15)、(17)和式(18)可得Ugα(k+1)和iα(k+2),将以上两个结果代入式(13),得到第k+1时刻两端柔直系统交流测输出电压uα(k+1),最后通过计算uα(k+1)与逆变器高压侧电压Udc的比值,得到逆变器所需的PWM占空比Dk+1。
本节所提改进无差拍控制策略优点在于:(1) 式(13)与式(6)、(7)相比,电流不会突变,同时电流偏差减少1/2,有限改善电流波形质量;(2) 无需计算k+2电流,将k时刻电流值与k+1时刻电流值直接关联;(3) 改善系统输出电流波形,减少电流总谐波失真(total harmonic distortion,THD)[19]。但改进算法默认连续采样时间间隔一致,因此一般适用于稳态环境,对于暂态环境还有待于进一步改善。
3 仿真验证及分析
为验证上文所提方法,搭建仿真系统,检验上述所提算法的正确性与有效性。系统主电路参数选取可参考文献[20],其中各器件具体参数如表1所示。

表1 系统主电路参数Tab.1 Parameters of main circuit system
3.1 仿真平台构建
本节所采用联合仿真平台将由NI Labview 2014 sp1与Starsim软件共同构成。其工作原理如下,Labview 2014 sp1负责数据采集、改进无差拍控制策略、两端并网控制器、向无源网络供电控制器等程序的编写;Starsim负责搭建背靠背柔性直流输电系统主电路包括2个电压源型换流器、2个变压器、2个电感以及2个交流配电网。在上位机中,通过桌面执行节点控件以及Starsim Design调用仿真程序、系统主电路,最终形成一个完整的仿真平台。
3.2 仿真结果分析
如图5所示,采用传统VSC三角波控制策略,利用NI控制器中高斯白噪声模块,在指令电流中加入指定谐波信号以模拟复杂的电网环境,在采用上述策略时,可以看出网侧电流发生明显畸变,图6利用快速傅里叶变换对此时网侧电流分析,图中3至7次谐波含量明显高于其余各次谐波之和,系统产生大量谐波,严重危害配电网运行。

图5 采用三角波控制时网侧电流波形Fig.5 The grid side current waveform of untaken measures

图6 采用三角波控制时网侧电流THDFig.6 The grid side current waveform THD of untaken measures
如图7所示,采用了传统无差拍控制策略,相比于图5,网侧电流波形趋于正弦,图8是此时网侧电流THD,图中3至7次谐波含量降低,3至7次谐波补偿率为60%,但仍较高,配电网运行仍受到危害。
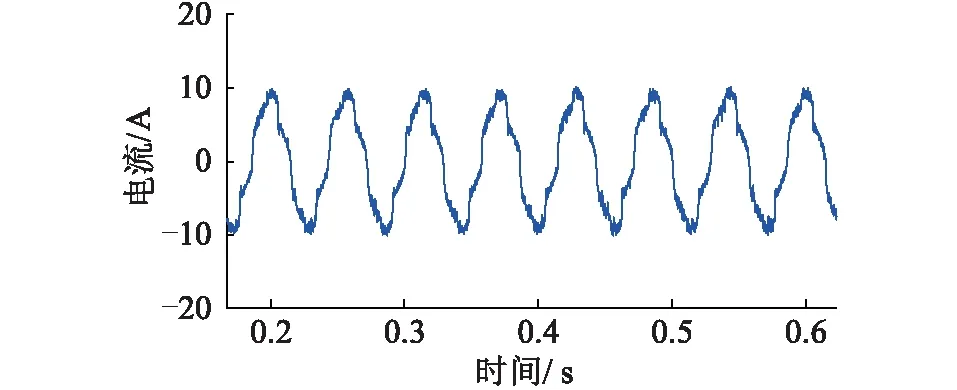
图7 采用传统无差拍后网侧电流波形Fig.7 The grid side current waveform of adopt tradition deadbead
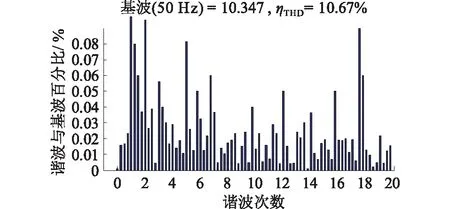
图8 采用传统无差拍后网侧电流THDFig.8 The grid side current waveform THD of adopt tradition deadbead
如图9、10所示,采用改进无差拍控制策略,从图10中看出,此时网侧电流THD为3.69%,图中3至7次谐波都得到有效抑制,3至7次谐波补偿率达到95%,系统运行安全性得到大大改善。
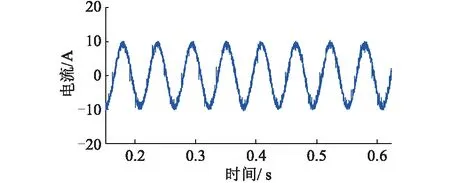
图9 采用改进无差拍后网侧电流波形Fig.9 The grid side current waveform of adopt improvement deadbead
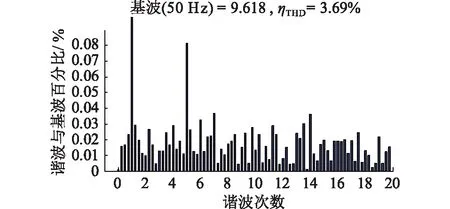
图10 采用改进无差拍后网侧电流THDFig.10 The grid side current waveform THD of adopt improvement deadbead
4 结语
文中以两端柔直输电系统为研究对象,建立两端柔直数学模型,研究系统基本运行方式以及电压源型换流器控制策略。考虑传统无差拍控制运用于VSC换流器时具有控制延时以及电流闭环控制响应性差等问题,提出一种改进无差拍控制策略,通过预测k+2时刻采样电流,解决上述缺陷。最后通过联合仿真,验证了所提方法的正确性与可靠性。未来可将文中所提改进方法与其他电能质量治理策略相结合,不仅拓宽了上述方法适用范围,而且可以进一步提高系统稳定性。
