北斗导航终端测试转台的非线性建模
2018-07-31李家斌谢璐璐宋丹玫
李家斌,谢璐璐,宋丹玫
(工业和信息化部电子第五研究所质量安全检测中心,广东 广州 510610)
0 引 言
随着北斗导航产品的应用及普及,其性能测试的需求也愈来愈多。北斗导航终端测试转台是导航产品测试系统的重要组成部分,可依据不同的测试需要做方位、滚动、俯仰旋转,检测北斗导航终端产品在不同方向的收发性能[1]6。北斗导航终端测试转台运行速度较低,其低速性能直接影响导航终端产品测试结果的正确度和精密度[2]101[5]11。本文主要对实验室专用北斗导航终端测试转台(以下简称测试转台)进行了建模仿真分析,得出摩擦力矩是影响导航性能测试转台低速性能的主要因素。同以往的转台建模不同,本文对测试转台的非线性摩擦力矩进行分析和补偿,采用工程实用的Stribeck模型进行线性化处理,转台建模更全面地考虑了实际非线性的影响,具有较好的工程实用意义。
1 导航终端测试转台理想建模分析
测试转台在低速条件下,三轴的耦合作用较小,对测试的影响可以忽略。三个轴的控制系统独立而且类似,可以选择其中一轴建模分析。本文以方位轴为例,对测试转台的方位轴框架进行建模分析。在理想情况下,对其建模也就是对执行元件——方位轴直流力矩电机的建模。

图1 转台方位轴直流力矩电机电枢回路电路图
方位轴直流力矩电机的电枢回路如图1所示。列出该电枢回路的电压平衡方程和感应电势方程式如下:
(1)
Ea=CeΦn=Keω
(2)
式中:Ua为输入的直流电压;Ia为电枢电流;Ra为电枢电阻;La为电枢电感;Ce为反电动势系数;Ke为反电动势系数;Φ为励磁磁通;ω为电机角速度;n为电机转速;Ea为反电动势。
列出转台电机电磁转矩方程式如下:
TF=CTΦIa=KTIa
(3)
式中:TF为电磁转矩;CT和KT为电磁转矩系数。
在直流力矩电机轴上,输出有电磁转矩、负载转矩、惯性转矩和电机轴本身存在的各种阻转矩,在这里统称为阻转矩Tf,综合电机轴上各种转矩可以得到电机轴转矩平衡方程如下:
TF=TL+Tf+Ti
(4)
(5)
式中:TL为负载转矩;Tf为综合阻转矩;Ti为电机轴惯性转矩;J为电机轴上转动惯量;β为电机角速度。
将上述各式取拉普拉斯变换,整理各式可得电机模型的状态方程如下:
可以根据上面的状态方程得到转台方位轴直流力矩电机理想的模型结构图,如图2所示。

图2 转台方位轴直流力矩电机理想模型框图
图中:θ为角速度经过积分后的角度。
得到转台方位轴理想的传递函数如下:
(6)
2 导航终端测试转台摩擦非线性分析
转台存在各种非线性环节,不仅仅是力矩电机,还包括驱动元件的死区,饱和非线性,各种干扰,轴系齿轮间的齿隙,各种摩擦因素等。一般的转台非线性环节包括有饱和、死区、间隙、摩擦等。结合本测试转台低速运行特点,忽略那些对转台建模影响较小的非线性因素,重点分析对转台低速性能影响大的因素——摩擦非线性环节。
摩擦非线性环节存在于任何具有相对运动的机械系统中,其对系统的性能有着严重的影响。在低速系统中,由于非线性轴承摩擦力相对较大,会使系统产生低速爬行现象。低速爬行不仅对控制系统低速性能有着严重的影响,还影响了电机轴的使用寿命。摩擦力具有强烈的非线性,它的大小与控制系统机械结构、输出角速度、表面润滑情况、轴系负载大小、运动情况有关,而且会随着运动状态的变化,温湿度的变化而变化。
本文采用工程实用的Stribeck摩擦模型对测试转台的摩擦非线性进行建模补偿[3]577,以寻求最贴近测试转台实际的转台模型。
3 导航终端测试转台摩擦非线性建模
在正常稳态条件,忽略那些环境因素的影响,摩擦力与相对速度的关系呈现一定的函数关系,将两者的函数关系绘制成曲线称为Stribeck曲线。该曲线揭示了两物体在润滑状态下,从接触到发生相对运动时摩擦力的变化过程。曲线示意图如图3所示。

图3 摩擦力与接触面相对速度关系曲线
图中a,b,c,d分别代表在润滑状态下,摩擦力随着接触面相对速度变换的四个阶段,也是摩擦力随着接触面相对静止到相互运动过程中的四个阶段[4]45[5]13。
(1)接触面弹性形变阶段,它随外力的变化而变化,属于静摩擦力。
(2)边界润滑阶段,此阶段对于低速爬行现象的产生有着很大关系。
(3)部分液体润滑阶段,此时接触面情况复杂,是属于最难建模的阶段。
(4)全液体润滑阶段。
由Stribeck曲线可知,摩擦力随相对速度变化是连续的,在克服静摩擦力后,摩擦力在低速下随着速度的增加而减小。Stribeck模型的数学描述[5]15如下:
(7)

Stribeck模型是按照Stribeck曲线实现的,实现了低速条件下摩擦力的连续。试验证明该模型能以90%的精确程度近似拟合真实的摩擦力。
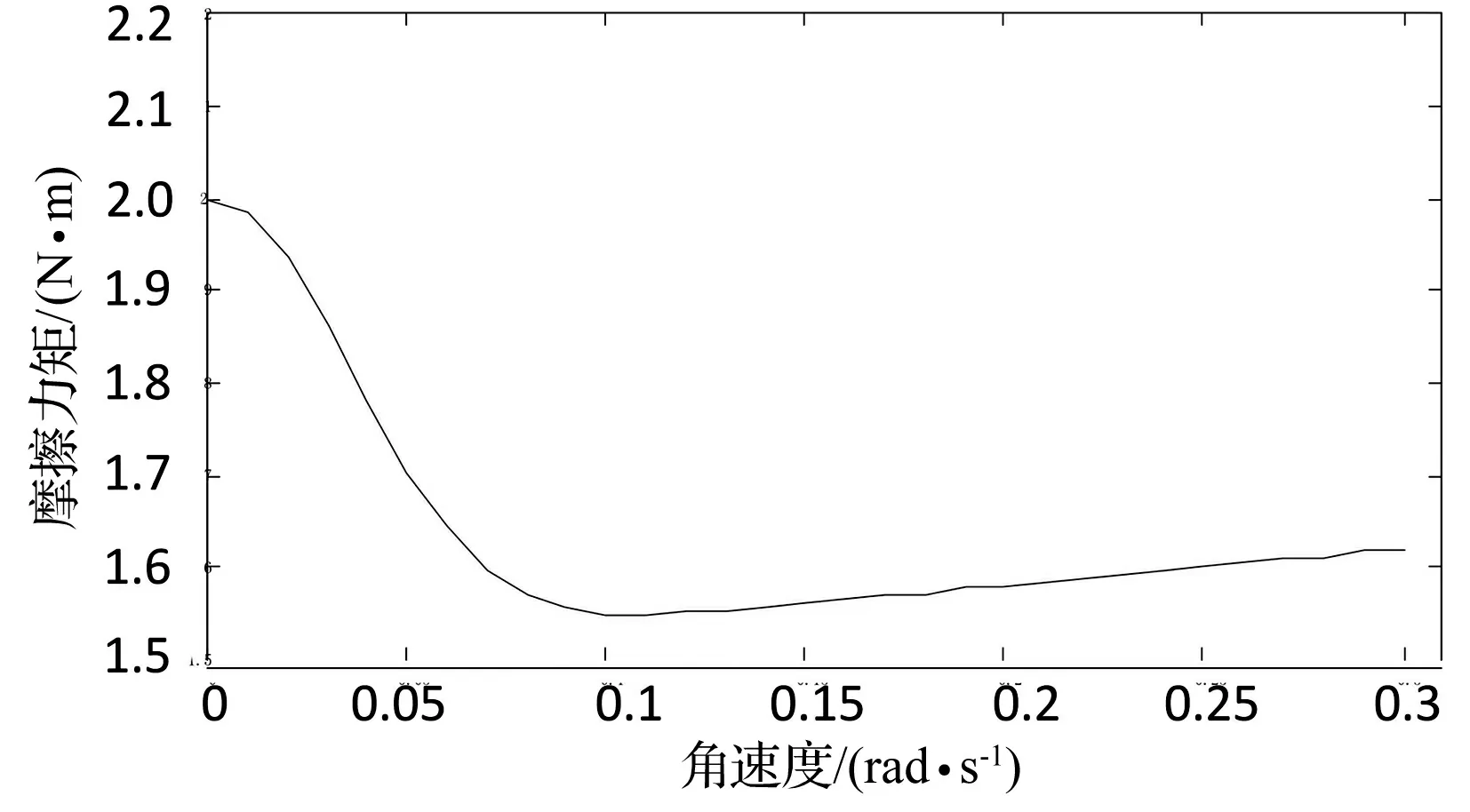
图4 转台摩擦力矩仿真曲线
由图4可知,仿真曲线十分接近Stribeck曲线,符合实际摩擦规律与过程,但曲线有着明显的非线性,可以考虑对其线性化进行分析,便于对测试转台的仿真补偿。将Stribeck模型转化为一种分段函数,实现摩擦曲线的线性化。该分段函数[5]16-17如下:
(8)
利用该线性模型,得到摩擦力矩线性仿真曲线如图5所示。

图5 转台线性摩擦力矩仿真曲线
图5曲线中,曲线1是利用Stribeck模型绘制出的非线性摩擦力矩曲线,曲线2是利用Stribeck模型转化来的分段函数模型绘制出的线性摩擦力矩曲线。由曲线可知,该线性化曲线较好地体现了Stribeck摩擦力矩模型的大致走势与规律,可以代替Stribeck模型曲线来进行建模分析。
将分段线性模型作如下变换:
(9)
(10)
将该线性摩擦模型代入测试转台理想模型,得到模型框图如图6所示。
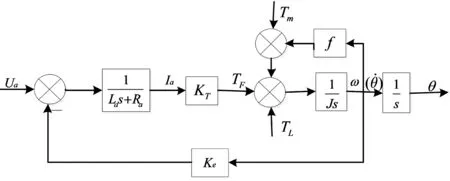
图6 带摩擦补偿的转台电机模型框图
由该模型可以得到加入摩擦环节后的转台直流力矩电机传递函数,如下式:
(11)
4 建模仿真结果分析

(12)
取输入信号为阶跃信号,幅值为5 V,没有摩擦环节,即Tm与f均为0,得到阶跃响应曲线如图7、图8所示。

图7 无摩擦的电机角速度阶跃响应图

图8 无摩擦的电机角度阶跃响应图
阶跃信号输入幅值5 V,代入摩擦环节(Tm=1,f=-1.5),其阶跃响应曲线如图9、图10所示。

图9 带摩擦的电机角速度阶跃响应图

图10 带摩擦的电机角度阶跃响应图
比较图7和图9,当系统加入摩擦模型后,角速度阶跃响应由稳定失去稳定;比较图8和图10,系统加入摩擦模型后,角度阶跃响应由线性变为非线性,而且出现了明显的死区,反应时间变长。总结可知,摩擦力对转台性能有很大的影响,特别是低速性能,会使系统产生死区,增大调节时间,加大稳态误差甚至使系统失去稳定。
5 结束语
本文对北斗导航终端测试转台进行了非线性分析建模,综合考虑了各类非线性因素的影响,并对摩擦模型进行了建模补偿。加入摩擦补偿后,转台模型仿真结果证明了摩擦力矩对转台低速性能有较大的影响,会造成死区,使系统失去稳定。该转台非线性模型对接下来研究北斗导航终端测试转台高精度的控制策略有较好的实际意义。
