MIMO下视阵列SAR倾角误差补偿算法

2018-07-31李葛爽楼良盛

测绘学报 2018年7期

刘辉，李葛爽，徐青，楼良盛

1. 华北水利水电大学资源与环境学院，河南郑州 450046； 2. 郑州市交通规划勘察设计研究院，河南郑州 450001； 3. 信息工程大学，河南郑州 450001； 4. 西安测绘研究所，陕西西安 710054

1996年，文献[1]首次提出了通过跨航向线性阵列天线实现三维成像的概念。这个里程碑式的想法标志着阵列SAR技术的诞生，拓展了SAR系统下视工作能力，有效解决了传统SAR体制机底盲区、几何失真和左右模糊等问题[2-5]。该技术在跨航向上稀疏布置收发分置的阵列天线[6-8]，采用天底观测的方式，分别通过合成孔径、脉冲压缩和波束形成技术实现观测对象方位向、高程向和跨航向的三维分辨。目前阵列SAR技术的研究主要集中在基于平台匀速直线运动假设的成像算法上[9-15]。但实际上，平台运动中不可避免会产生位置偏移和姿态变化，从而造成天线相位中心的偏移，影响高分辨率阵列SAR三维成像质量。因此为了保证成像所需的相位精度，分析平台位移、姿态变化的误差补偿方法具有重要的意义。

在国外，法国ONERA实验室研制了基于BUSARD滑翔机的DRIVE Project，并利用POS系统获取的位置和姿态信息辅助完成侧视和正视成像试验，但没有公布其运动补偿方案和结果[16-17]。德国FGAN-FHR的ARTINO系统分别利用DGPS、IMU组合设备和激光/CCD装置，分析姿态角误差和机翼振动对成像的影响，但前者也未公布补偿方案和结果，后者虽提出了补偿方法但未考虑目标空变性影响[18-21]。2010年后国外学者再无公开发表过阵列SAR相关研究成果，目前公开发表的文献主要来自国内学者。2009年，文献[22]提出了下视聚束三维SAR PGA补偿方法，但相位误差非空变假设不符合下视阵列SAR观测几何；2012年，文献[23]研究了机载三维SAR多通道联合自聚焦补偿方法，但忽略了目标空变性影响；文献[24]分析了相位中心偏差对机载阵列天线下视3D-SAR成像的影响。2015年，文献[25—26]研究了机载三维SAR平动误差、偏航角误差补偿方法。但这些研究都是从信号角度分析的，与测绘关联甚少。

本文从测绘角度切入，引入传统光学摄影测量的外方位元素，建立了外方位元素整体误差模型。发现3个线元素误差导致的相位中心偏移在一个线性阵列的不同阵元之间是一样的，可以借助传统的SAR运动补偿方法来实现[27]。3个角元素误差导致的相位中心偏移在阵元间则不同，偏角误差不会影响天线阵元到地面点的距离历程，对成像误差没有影响[23]；旋角误差会同时引入沿航向和跨航向两个方向的运动误差，补偿较为复杂；倾角误差并不会引入沿航向的运动误差，且在跨航向-高程向平面内的成像结果聚焦正确，仅仅位置发生了旋转。进一步假设除倾角外的其他外方位元素均为0时，推导了倾角误差模型，提出了基于倾角误差的MIMO下视阵列SAR误差补偿方法，最后通过仿真试验验证了方法的有效性。

1 外方位元素整体误差模型

为了保障阵列天线SAR的工程应用，引入POS所能获得的真实数据形式来分析下视阵列SAR误差补偿问题。如图1所示，POS中的IMU(inertial measurement unit，惯性测量单元)坐标系为原点在IMU中心，X轴指向航向，Y轴指向飞机右侧，Z轴向下的右手直角坐标系。输出的POS数据是基于用户定义的参考坐标系，通常IMU坐标系就是默认的参考坐标系。

图1 IMU外形Fig.1 IMU appearance

IMU系统所获得的3个角度(偏航角、俯仰角、横滚角)是参考坐标系(Ob-X′Y′Z′)相对于北东地坐标系(On-XYZ)的旋转角。北东地坐标系先绕Z轴顺时针旋转偏航角κ，再绕已转了κ角的Yκ轴顺时针旋转俯仰角ω，最后绕已转了κ角和ω角Xκω轴顺时针旋转横滚角α，得到的坐标轴方向与参考坐标系完全相同。其中，角度符号定义满足右手规则：右手握住旋转轴，大拇指指向旋转轴正向，其余4指的指向就是旋转角度的正方向。

由上述转换关系可得北东地坐标系与参考坐标系之间的关系

(1)

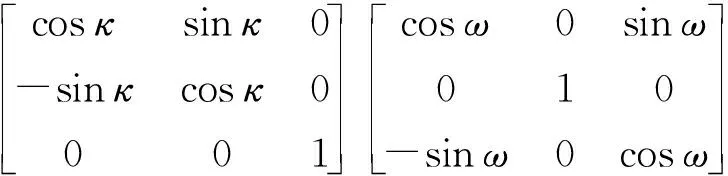
(2)

对等式(1)两边求逆可得

(3)

矩阵Rα、Rω、Rκ是正交阵，因此有

(4)

通过式(4)可发现，该转换关系类似于光学摄影测量中外方位元素“以X轴为主轴的转角系统”。因此，为了能够充分利用POS所获得的数据信息，可以借鉴光学摄影测量中外方位元素的思想，为阵元位置引入3个线元素误差和3个角元素误差。

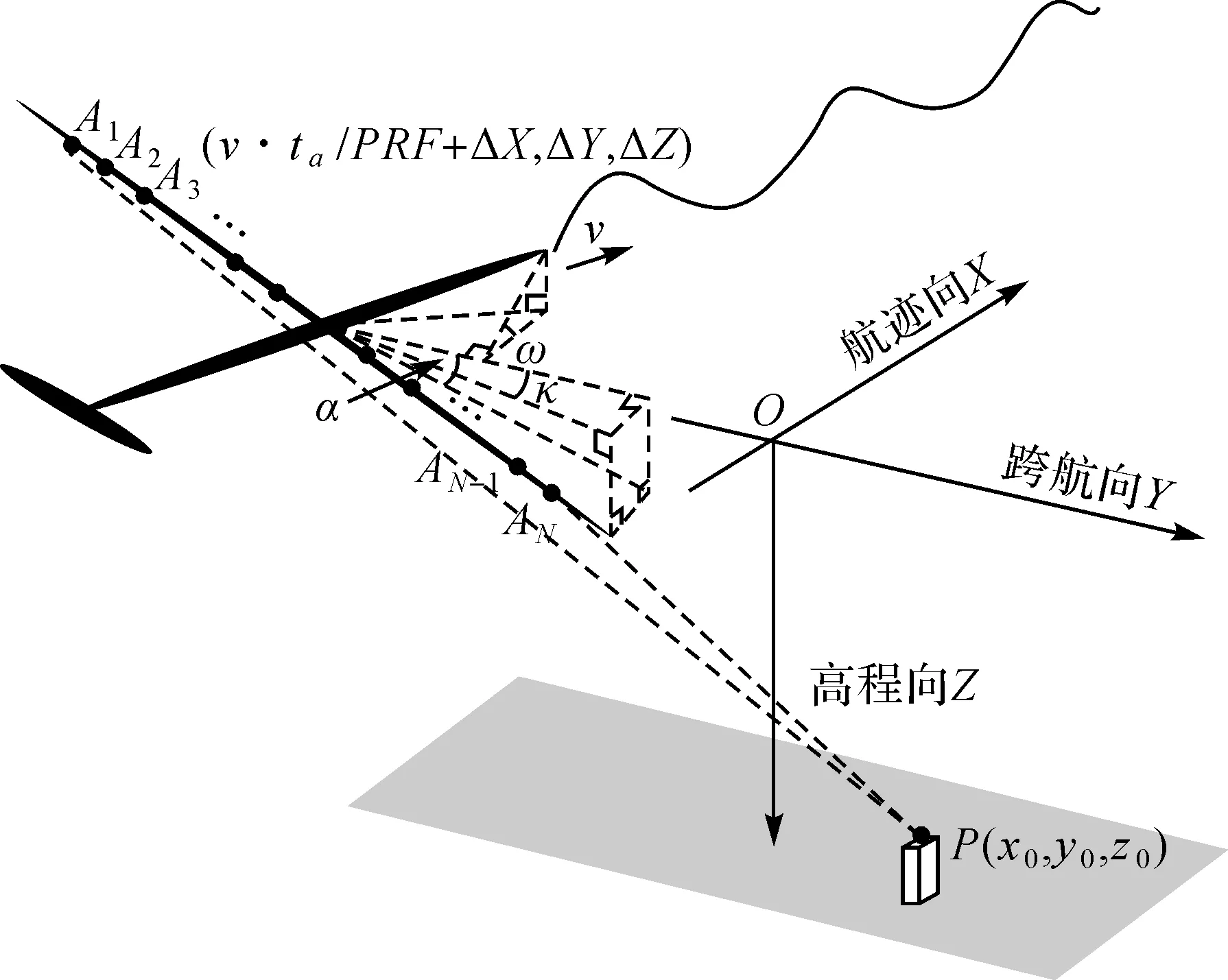
图2 外方位元素误差示意图Fig.2 Sketch map of elements of exterior orientation errors

由IMU系统的旋转角关系可知，3个角元素误差引入的旋转矩阵为

(5)

借鉴光学摄影测量中“空间相似变换公式”，除去比例缩放因子后可得发射阵元的实际坐标

(6)

式中，v为载机速度；ta为方位向慢时刻；PRF为脉冲重复频率；ΔX、ΔY和ΔZ分别为方位向、跨航向和高程向的坐标增量。

同理可得接收阵元的实际坐标

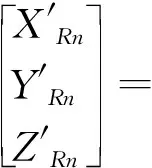
(7)

式中

(8)

理想情况下，等效相位中心对应目标点的距离历程R为

(9)

(10)

根据泰勒近似公式，将两个距离分别在慢时间ta0=x·PRF/v(x为方位向坐标)处展开可得

(11)

(12)

式中

(13)

进一步联立式(11)和式(12)可计算得到回波相位误差ΔΨ为

(14)

式中，λ为波长。

由式(14)可知，回波信号中的相位误差相当复杂，不仅与外方位元素的6个量有关，还具有3个方向的空变性，具有严重的耦合现象，需进行分解，逐个研究单元素误差补偿方法。

2 倾角误差模型

为了方便分析，假设下视阵列SAR系统只存在倾角误差αy，如图3所示。跨航向分布的n个线阵阵元经过等效相位中心误差补偿后可以等效为阵元间隔均匀的等效虚拟阵列，等效相位中心坐标为(x,yn,0)，目标点P的坐标为(x0,y0,z0)，坐标轴向仍然沿用图2表述。

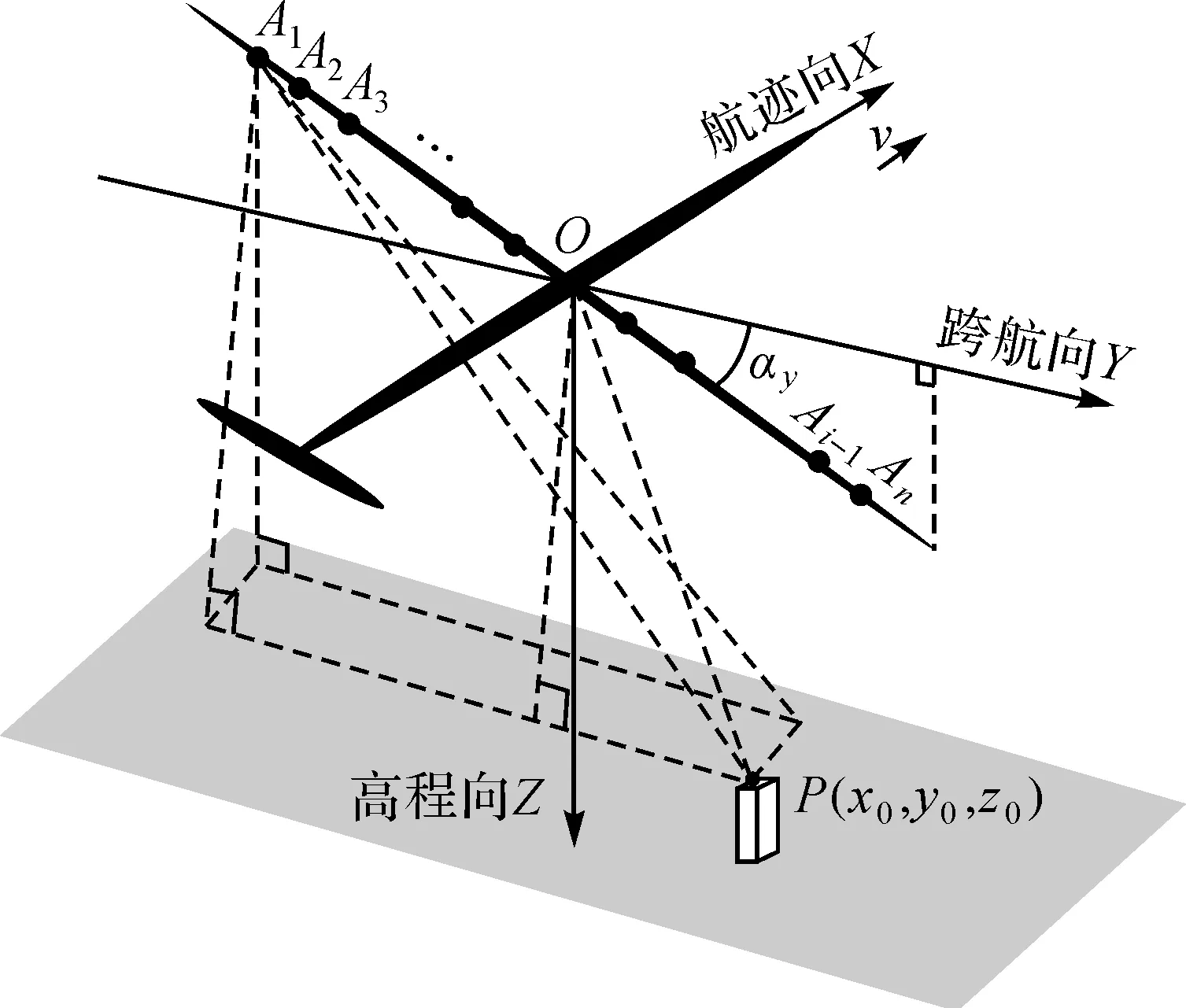
图3 MIMO下视阵列SAR倾角误差模型Fig.3 Inclination angle error model of MIMO downward-looking array SAR

借鉴光学摄影测量外方位角元素旋转矩阵的思想，将平台坐标系绕X轴旋转，则旋转前后等效相位中心的坐标有如下关系

(15)

因此旋转αy角后，等效相位中心的坐标(x′,y′,z′)变为(x,yncosαy,ynsinαy)。理想情况下，等效相位中心到目标点的距离R为

(16)

(17)

则由倾角误差引起的距离误差ΔR为

(18)

式中

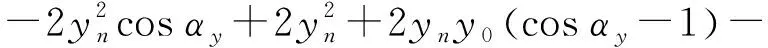
2z0ynsinαy=2y0yn(cosαy-1)+2z0ynsinαy

(19)

代入式(18)可得

(20)

由式(20)可知，距离误差ΔR并未在x方向上引入误差，但受目标坐标y0和z0的空变影响，不能直接对全孔径进行补偿处理，需要考虑子孔径补偿方法。经解调和匹配滤波后，回波Echo(t,x,yn)如式(21)所示。

Echo(t,x,yn)=sinc[t-2(R+ΔR)/c]exp(jΨ)=

sinc[t-2(R+ΔR)/c]

exp(-j4π(R+ΔR)/λ)

(21)

式中，sinc为sinc函数；Ψ为回波相位误差。

3 倾角误差补偿方法

MIMO下视阵列SAR地形重建最直接的方法是利用等效相位中心原理，将多发多收收发分置的回波信号转化为收发共用的情况后，再沿用传统SAR二维成像技术和波束形成技术实现三维成像。当载机平台受外界环境等影响产生运动误差后，成像补偿方法习惯将该误差利用三角函数转换为沿航迹方向和雷达视线方向位置位移来分别处理。沿航迹方向非均匀采样问题通常用时域插值重采样方法解决；雷达视线方向补偿则多忽略目标空变性影响，直接进行全孔径补偿处理。首先采用场景中心线作为参考目标对整个场景进行补偿，然后对参考线以外的其他距离目标回波的残留相位误差进行补偿。但从倾角误差模型来看，距离误差ΔR受目标坐标y0和z0的空变影响，不能直接进行全孔径补偿。

为了消除距离误差的空变影响，将式(21)中的相位分别对x和yn求偏导，得到航迹向波数kx和跨航向波数ky

(22)

(23)

联立式(22)、式(23)和式(17)

(24)

利用菲涅尔定理化简，并忽略阵元长度小值，可得

(25)

代入式(24)可得

(26)

将式(25)和式(26)代入式(20)可得距离误差

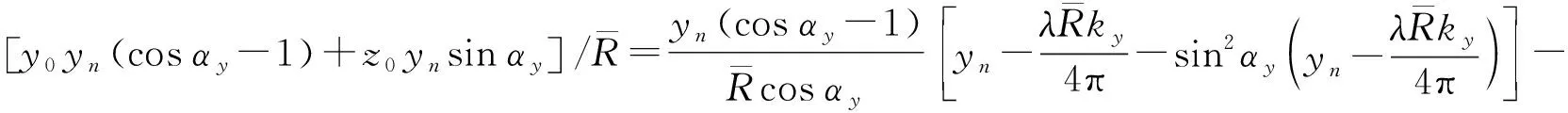
(27)

由式(27)可知，距离误差与目标位置无关，即消除了目标空变影响。将其分为ΔR1和ΔR2两部分，ΔR1与波数无关，可在回波的三维空域中首先对其进行补偿，称为一次补偿。ΔR2与波数相关，可在二维波数域中分块计算，称为二次补偿。

首先由ΔR1构造滤波器Hα1，进行一次补偿。

Hα1=exp(-j4πΔR1/λ)=

(28)

再将补偿完ΔR1的回波数据做航迹向和跨航向傅里叶变换，变换到该二维波数域，并沿航迹向和跨航向均匀分为M和N段，获得M×N个子块，每个子块用中心波数kx-ic和ky-jc代替kx和ky计算距离误差ΔR2-ij为

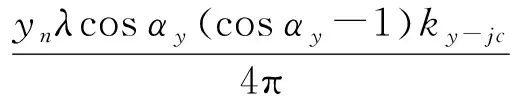
(29)

将每个子块补零并扩展到原尺寸后，再做航迹向和跨航向傅里叶逆变换，以及距离向傅里叶变换，得到航迹向和跨航向二维空域，距离向波数域回波

(30)

式中，kr为距离向波数；krc为中心波数；Br为带宽。

将式(30)乘以滤波器Hα2来补偿ΔR2-ij引起的相位误差，称为二次补偿。再做距离向傅里叶逆变换，转换到三维空域，把每个子块补偿的数据直接相加，得到最终回波。接着使用三维RD算法进行成像即可得到理想的成像结果。倾角误差补偿及成像流程如图4所示。

(31)

图4 倾角误差补偿及成像流程Fig.4 Flow of inclination angle error compensation and imaging

4 试验与分析

4.1 仿真地形试验

本文仿真了一个具有3个山峰、两个山谷的山区地形，采用2发80收的MIMO模式，利用表1中的仿真参数对具有倾角误差的MIMO下视阵列SAR系统进行三维成像试验。图5(a)和5(b)分别给出原始仿真地形的三维图和二维图，最大高程为48.626 0 m，最小高程为-39.297 7 m。

表1 载机系统仿真参数

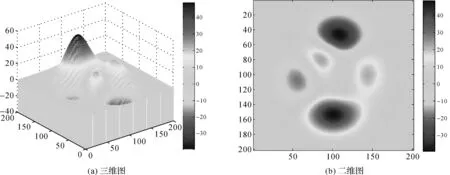
图5 原始仿真地形Fig.5 Original simulation terrain

航测规范中要求倾角一般不大于2°，最大不超过3°，因此仿真试验时若故意把倾角加大来分析，最终结果并没有意义。本文在仿真过程中选取最大倾角为3°，如图6所示。理想情况下，在YOZ平面阵元的位置为(nd,0)(n代表第n个等效虚拟阵元，d代表等效虚拟阵元之间的间隔)，当载机飞行过程中发生了倾角误差时，阵元的位置在Y方向和Z方向则会分别产生分量ndcosαy和ndsinαy。

图6 倾角误差带来阵元位置变化示意Fig.6 Sketch map of array element position change caused by inclination angle error

补偿前，阵列SAR原始回波数据如图7(a)所示。成像处理后实现斜距、方位和角度三维分辨，图7(b)、图7(c)、图7(d)分别给出方位-角度平面、角度-斜距平面和方位-斜距平面的切面图，从目视效果来看，与角度相关的切面图均出现明显的整体位移。将成像结果根据角度、斜距与高度、地距之间的转换关系，按照与原始地形相同的格网间隔插值规划到同一坐标系后，可得到三维成像结果图7(e)，很明显仿真区域整体产生了偏移，且进一步导致观测区域边缘产生较大误差。图7(f)给出了成像结果的二维图，与图5(b)相比，整体效果欠佳，由-39.30至48.63的高程范围增大到-39.00至77.13之间，误差较大。

经等效相位中心相位误差补偿后的回波数据如图8(a)所示，振幅大小有了明显地缩小，有效补偿了相应回波。经过成像处理后，图8(b)、图8(c)、图8(d)分别给出补偿后方位-角度平面、角度-斜距平面、方位-斜距平面的切面图。方位-角度平面由图7(b)中跨航向的15 m～125 m区域校正到25 m～135 m区域，角度-斜距平面由7(c)中沿航向的10 m～120 m区域校正到30 m～140 m区域。将成像结果按相同格网间隔插值规划到地距、方位、高度坐标系后，得到图8(e)所示的三维成像结果，补偿前整幅图像上出现的大量毛刺信息消失了。与图7(f)相比，成像结果二维图8(f)更能明显地展示出改善效果，3个山峰和2个山谷都基本恢复了本来形貌。

图7 仿真地形补偿前结果图Fig.7 Pre-compensation result maps of simulation terrain

图8 仿真地形补偿后结果图Fig.8 Compensated result maps of simulation terrain

为了进一步定量分析补偿效果，将补偿前的成像结果(图7(e))与原始地形(图5(a))作差分处理后可得差分图9(a)，在山峰和山谷地区出现多个明显的细胞状误差区域；统计其直方图10(a)，差值在-31.051 m至25.121 m之间变换，且有大量不在0附近的值，误差较大。将补偿后的成像结果(图8(e))与原始地形(图5(a))作差分处理后可得差分图9(b)，很明显高程误差得到了较好地控制；统计其直方图10(b)，差值缩小至[-4.356 m，4.205 m]区间，且主要集中在-1 m至1 m之间。但从整体上来看，图面信息仍较乱，尤其在几个山峰和山谷地区，有大量绕着山势类似等高线的误差区域。究其原因，除了跨航向分辨率的局限以外，主要还是距离计算不准确所致，后续可考虑借助控制信息校正相应距离值。

图9 仿真地形的成像结果与原始场景差分图Fig.9 Difference map between imaging results and original scene of simulation terrain

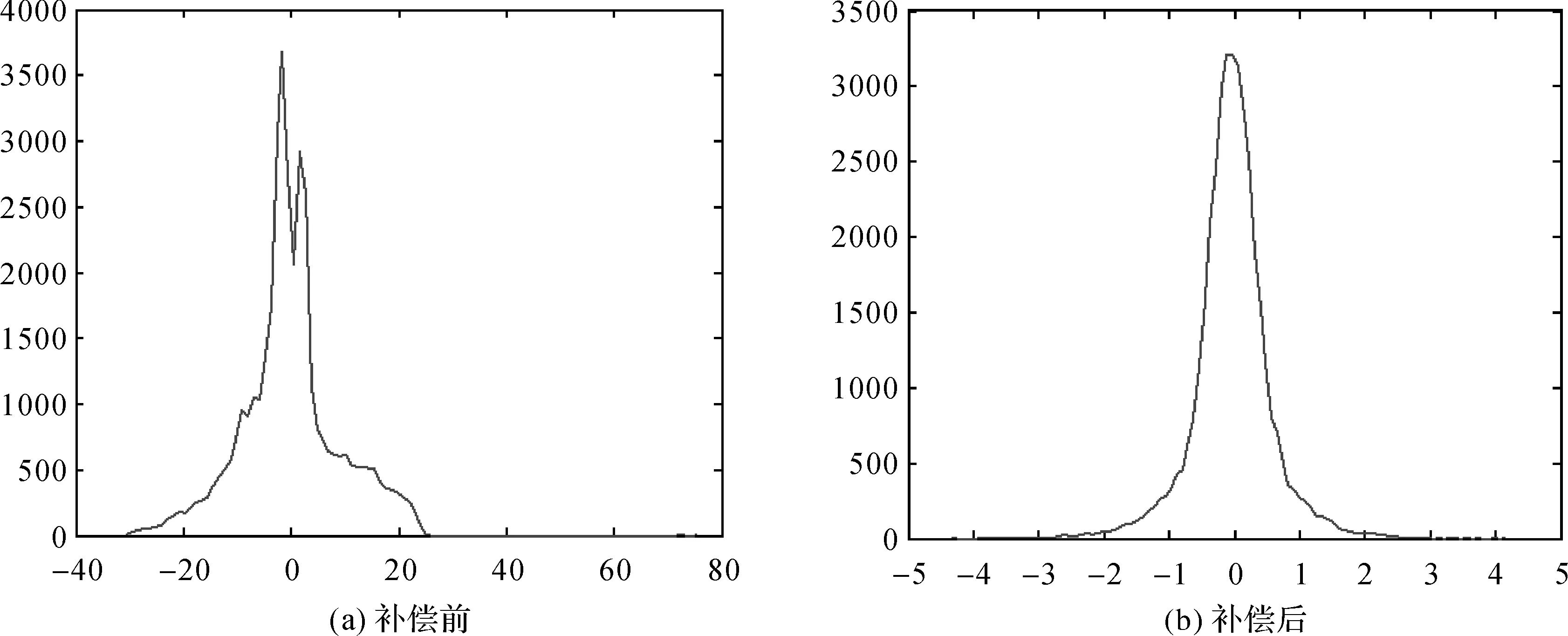
图10 差分结果直方图Fig.10 Differential results histogram

表2定量统计了补偿前后成像结果的高程误差均值、标准差和整个场景高程误差在半个分辨率之内的概率。补偿后，前两个指标有了明显下降，最后一个指标又有大幅提高，这足以说明补偿方法的有效性。

表2 成像结果定量指标统计

4.2 SRTM DEM真实地形试验

为了进一步验证MIMO下视阵列SAR倾角误差补偿方法的有效性，本文选取青藏高原地区30 m分辨率的SRTM DEM为原始场景，仍然采用2发80收的MIMO模式进行试验。图11给出对原始DEM重采样为0.5 m格网间距后截取的200×200 m大小的DEM二维图和三维图。最大高程为4 931.2 m，最小高程为4 712.1 m。由于地形高程的抬高，表1中平台高度也相应调整为5200 m，其他参数不变。

图11 SRTM DEM真实地形Fig.11 SRTM DEM real terrain

补偿前的三维成像结果如图12所示，不仅整体位置发生偏移；大量高程值也不准确，尤其在跨航向上发生偏移的反方向表现明显。利用本文方法补偿后，三维成像结果如图13所示，基本恢复了真实DEM的本来形貌。为了能更加直观地表现补偿效果，分别将补偿前后的成像结果与原始SRTM DEM作差分，可得图14，误差范围从[-151.56，133.15]缩小到[-9.99，9.09]。统计表2中的3项指标，高程误差均值从-24.05降到-0.03；高程误差标准差从49.88降到1.82；整个场景高程误差在半个分辨率之内的概率从2.38%提高到80.28%。无论从目视效果，还是统计量都充分证明了补偿方法的有效性。

5 结束语

阵列天线子阵相位中心高精度测量是MIMO下视阵列SAR系统的重点。系统平台实际运动中产生的位置偏移和姿态变化会造成天线相位中心的偏移，影响高分辨率阵列SAR三维图像质量。本文结合POS真实数据形式，引入传统光学摄影测量的外方位元素，提出了基于倾角误差的MIMO下视阵列SAR误差补偿方法。该方法借助回波相位在沿航向和跨航向的偏导值，以及存在倾角误差时的斜距值联立求解，消除了倾角误差的空变影响，采用二维波数域分块计算距离误差，空域逐块补偿的方式完成了三维成像。通过仿真试验验证了本文方法的有效性。

后续研究中，需进一步评定误差补偿后的精度，通过对阵列SAR数据处理中若干非理想因素进行补偿和影响分析，明确指出对载机POS的要求。