致密储层应力敏感性分析及裂缝参数优化

孙元伟 ，程远方 ，张卫防 ，时凤霞 ，印树明

（1.中国石油大学胜利学院油气工程学院，山东 东营 257061；2.中国石油大学（华东）石油工程学院，山东 青岛 266580；3.中国石化胜利西南钻井分公司，山东 东营 257000）

0 引言

近年来，致密油气资源逐渐成为增储上产的重要阵地［1］。致密储层具有岩性致密、渗透率低并且天然裂缝发育等特征［2-4］，需要体积压裂改造形成多条人工裂缝及次生裂缝才能获得经济性油流。体积压裂改造后，致密储层可分成2个区域：一是人工裂缝及次生裂缝网络发育、渗透率较大的改造区域；另一个是压裂液无法波及、保持储层原有物性特征的未改造区域。微地震监测数据证明了这点。

致密储层未改造区域由于储层较致密、裂缝较少，应力敏感性较小；改造区域在体积压裂后发育复杂次生裂缝网络，应力敏感性较大，导致次生裂缝和渗透率发生变化［5-9］，对裂缝参数优化设计的结果产生较大的影响。

在致密储层压裂优化设计过程中，传统模型认为，随着裂缝长度的增加，近裂缝改造区域面积增加，但是忽略了改造区域内应力敏感性的增强［10-14］，也没有考虑其对产量的影响［15-16］。因此，笔者基于致密储层不同区域应力敏感性对储层渗透率的影响，建立了致密储层水平井体积压裂3D渗流模型，采用有限元的方法对模型进行求解，并耦合分析了体积压裂后储层应力敏感性和裂缝长度对产能以及渗透率分布的影响，进而对应力敏感特性储层进行裂缝长度优化。

1 水平井体积压裂3D渗流模型

1.1 模型基本假设

致密储层水平井体积压裂3D渗流模型如图1所示。其建立过程中进行如下假设：1）水平井位于致密储层中心，储层渗透率各向异性，天然裂缝发育，考虑应力敏感性的影响；2）人工裂缝周围的复杂次生裂缝网络发育，形成物性好、应力敏感性较强的改造区域（改造区域的大小可以根据微地震监测数据、生产井测井资料等进行计算）；3）人工裂缝为有限导流能力裂缝，可设置为不等间距、不等半长；4）流体在储层中流动为三维流动，在裂缝中的流动为二维流动。

图1 致密储层水平井体积压裂3D模型示意

1.2 数学模型

根据以上假设，建立致密储层水平井体积压裂三维渗流数学模型。

未改造区域渗流数学模型：

式中：p为储层压力，105Pa；Kmx为未改造区域x方向渗透率，10-3μm2；Kmy为未改造区域 y 方向渗透率，10-3μm2；Kmz为未改造区域 z方向渗透率，10-3μm2；μ为流体黏度，mPa·s；φm为未改造区域孔隙度；Cm为未改造区域综合压缩系数，10-5Pa-1；t为生产时间，s。

改造区域次生裂缝网络发育，由于裂缝发育分布情况复杂且无法采用数学方法进行定量描述，实际描述中采用等效渗透率的方法进行处理［17］。根据岩心实验等手段获得致密储层次生裂缝网络发育区域的等效渗透率，代入渗流控制方程，可得：

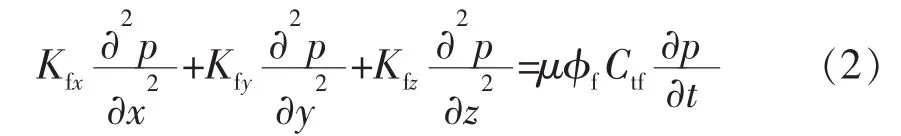
式中：Kfx为改造区域 x 方向渗透率，10-3μm2；Kfy为改造区域y方向渗透率，10-3μm2；Kfz为改造区域 z方向渗透率，10-3μm2；φf为改造区域孔隙度；Ctf为改造区域综合压缩系数，10-5Pa-1。

人工裂缝中渗流数学模型：

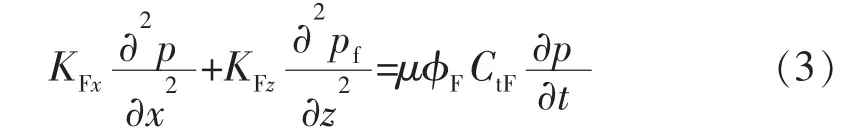
式中：KFx为人工裂缝 x 方向渗透率，10-3μm2；KFz为人工裂缝z方向渗透率，10-3μm2；φF为人工裂缝孔隙度；CtF为人工裂缝综合压缩系数，10-5Pa-1。

改造区域应力敏感性对渗透率的影响为

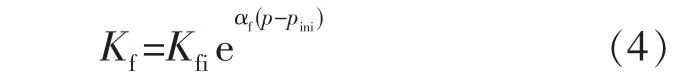
式中：Kf为改造区域渗透率，10-3μm2；Kfi为改造区域初始渗透率，10-3μm2；pini为储层初始压力，105Pa；αf为改造区域应力敏感系数，10-5Pa-1。

未改造区域应力敏感性对渗透率的影响为

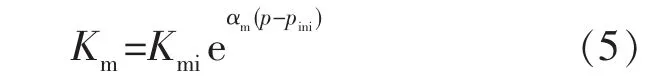
式中：Km为未改造区域渗透率，10-3μm2；Kmi为未改造区域初始渗透率，10-3μm2；αm为未改造区域应力敏感系数，10-5Pa-1。

1.3 模型求解

致密储层水平井体积压裂3D渗流数学模型中包含了3组强非线性偏微分方程组，无法得到解析解或半解析解，因而采用有限元方法对其进行求解。基于Delaunay三角剖分的Watson算法［18］，采用有限元结构化三角形网格生成的自适应技术，根据人工裂缝的尺寸对致密储层进行了网格划分，其中人工裂缝处网格尺寸最小值设置为裂缝宽度的1/3，如图2所示。在网格划分的基础上，将储层未改造区域、改造区域的3D有限元方程和人工裂缝区域的2D方程组合成系统，利用COMSOL有限元求解器进行求解。

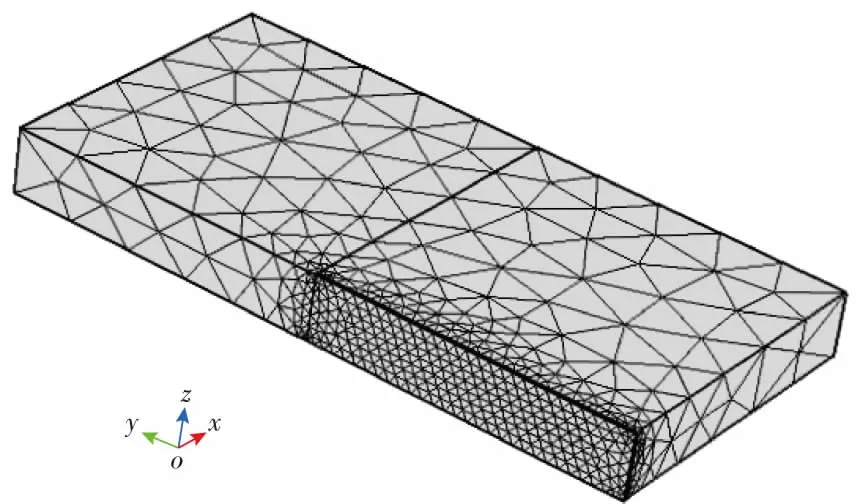
图2 致密储层网格划分示意

2 模型实际应用

针对典型致密储层——长庆鄂尔多斯盆地某区块，通过岩心测试及试井解释等方式获得其基础参数（见表1）。结合本文模型，研究储层应力敏感性、储层裂缝穿透比等因素对产量以及储层区域渗透率的影响，并对应力敏感储层进行裂缝长度优化。

表1 长庆鄂尔多斯盆地某区块基础参数

2.1 储层产量变化规律

2.1.1 应力敏感性的影响

应用岩心实验等手段，改变应力敏感系数的大小，得到改造区域应力敏感性对水平井产量影响的曲线（见图3）。

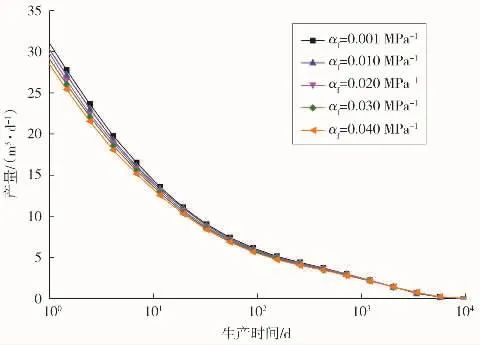
图3 应力敏感性对产量的影响

从图3可以看出，当裂缝穿透比相同时，改造区域应力敏感性对致密储层水平井体积压裂早期产量影响较大，应力敏感系数越大，早期产量越小；当生产时间较长时，改造区域应力敏感性对储层产量的影响逐渐减小，其原因是储层渗透率变化符合指数模型，生产后期渗透率变化速度逐渐减缓，因而改造区域应力敏感性对产量的影响也逐渐减小。

2.1.2 裂缝穿透比的影响

考虑致密储层应力敏感性的影响，改变裂缝穿透比γ的大小，得到裂缝穿透比对应力敏感储层产量的影响曲线（见图4）。

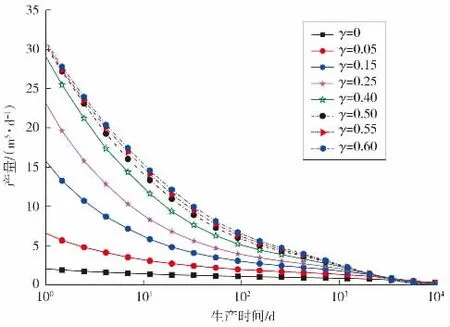
图4 裂缝穿透比对产量的影响

从图4可以看出，当裂缝穿透比较小时，裂缝穿透比对裂缝早中期产量影响较大，增加裂缝穿透比可以大幅度提高裂缝产量。当裂缝穿透比大于0.40时，应力敏感性对产量影响逐渐加大，继续增加裂缝穿透比对裂缝产量影响逐渐减小，甚至造成产量的降低。

2.2 储层渗透率分布规律

分别计算不同改造区域应力敏感系数和裂缝穿透比下的储层渗透率。不同应力敏感系数及裂缝穿透比对储层渗透率分布的影响如图5、图6所示（以单裂缝控制面积的1/4为例进行分析，裂缝延伸方向为竖直方向）。

图5 应力敏感性对储层渗透率分布的影响

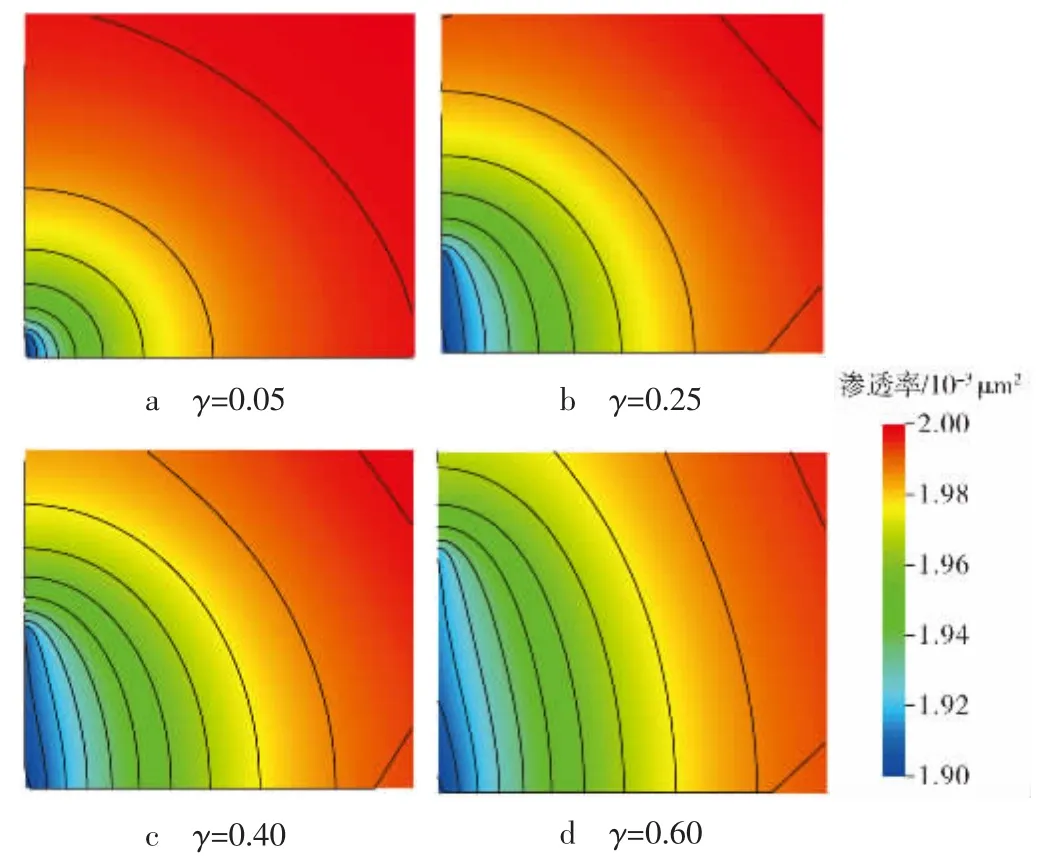
图6 裂缝穿透比对储层渗透率分布的影响

图5中对比了不同应力敏感系数对渗透率分布的影响。由图可以看出：改造区域应力敏感系数主要影响近井地带渗透率的大小，随着应力敏感系数增加，近井地带渗透率下降幅度和下降范围进一步扩大；改造区域应力敏感性对储层渗透率分布形态影响很小，裂缝周围区域渗透率等值线为同轴椭圆形，椭圆轴长基本相同，且沿着裂缝方向渗透率下降幅度远远大于垂直于裂缝方向。

图6对比了不同裂缝穿透比对渗透率分布的影响。由图可以看出：当裂缝穿透比发生变化时，储层渗透率的分布形态也发生了较大的改变，但相对于应力敏感性的影响偏小；裂缝穿透比主要对渗透率椭圆形等值曲线的长轴长度产生较大影响，裂缝穿透比越大，轴长越长，对短轴长度影响较小。综合来说，随着裂缝穿透比增加，近井地带渗透率下降范围进一步扩展，下降幅度增加较小，储层渗透率的变化趋势与压力的变化相同。

2.3 裂缝长度优化

常规储层中裂缝越长产量越高，且随着裂缝长度的增加，增加单位裂缝长度的增产量越小。对于应力敏感储层，增加裂缝长度同时，扩大了改造区域应力敏感性对增产的不利影响，增加单位裂缝长度的增产量要小于不考虑应力敏感性的增产量，因此在裂缝长度优化设计中需要考虑应力敏感性的影响。

图7为改造区域应力敏感系数为0.010 MPa-1时，不同裂缝穿透比情况下10 a的累计产量。

由图7可以看出：在裂缝穿透比较小时，增加裂缝穿透比可以明显提高裂缝产量，此时应力敏感性对产量的影响较小；当裂缝穿透比大于0.40时，继续增加裂缝长度，产量不再增加，因而此时应适当控制裂缝的长度。实例应用表明，当应力敏感系数为0.010 MPa-1，裂缝穿透比为0.40时，可以取得最佳的增产效果。

3 结论

1）裂缝穿透比较小时，裂缝穿透比对裂缝的早中期的产量影响较大。当裂缝穿透比大于0.40时，应力敏感性对产量的影响逐渐加大，继续增加裂缝穿透比对裂缝产量的影响逐渐减小，与常规储层相比，最佳的裂缝穿透比明显减小。

2）随着裂缝穿透比增加，近井地带渗透率下降范围进一步扩展，下降幅度增加较小。

3）利用模型对实际油藏进行压裂优化，当应力敏感系数为0.010 MPa-1，裂缝穿透比为0.40时可以取得最佳增产效果。