致密油藏体积压裂水平井半解析渗流模型

2018-07-30任宗孝王翔崔守凯杨鲜鲜杨强强毕刚

断块油气田 2018年4期

任宗孝，王翔，崔守凯，杨鲜鲜，杨强强，毕刚

（1.西安石油大学石油工程学院，陕西西安 710065；2.西安石油大学陕西省油气井及储层渗流与岩石力学重点实验室，陕西西安 710065；3.中国石油西南油气田分公司勘探事业部，四川成都 610041；4.中国石油青海油田分公司采油二厂，甘肃敦煌 736202；5.中国石油青海油田分公司开发处，甘肃敦煌 736202）

0 引言

国内致密油资源储量丰富，得益于水平井以及大规模压裂技术的发展，使致密油藏成为了一种现实的接替能源［1-2］。致密油藏特殊的地质条件，导致在大规模水力压裂过程中容易形成复杂的裂缝网络［3-4］。裂缝在空间上任意交错导致地层渗流发生了较大的变化，近年来国内外学者建立了大量的数学模型，模拟复杂缝网条件下分段压裂水平井的渗流问题。这些数学模型大致可分为解析模型、半解析模型以及数值模型等3类，每类模型均有其优缺点。

2014 年，W.T.Zhou 等［5］建立了体积压裂水平井产能模型，可将复杂缝网进行线性离散，且能考虑每段裂缝不同的几何及流动属性；但没有考虑裂缝交叉时产量的“劈分”流动。2015 年，W.D.Wang 等［6］在 Ozkan［7］三线性物理模型的基础上，考虑分形流动建立了非常规油藏体积压裂水平井产能模型，并将油藏渗流划分为 5 个流动阶段。2015 年，W.Luo 等［8］基于 Ozkan［9］面源函数建立了封闭板状无限大油藏体积压裂直井渗流模型，应用坐标转换方法考虑了裂缝倾角，但同样没考虑裂缝交叉时产量“劈分”流动的问题。2015年，Z.M.Chen 等［10］基于 Ozkan［9］面源函数建立了主裂缝上含有次生裂缝的纵横垂直复杂缝网渗流模型，其优点是每条裂缝的渗流属性以及尺寸可以不同。2016年，任宗孝等［11］基于体积源函数［12］建立了纵横垂直交错缝网渗流模型，但文中垂直缝网的假设过于理想。

本文基于改进的Ozkan面源函数［13］建立了致密油藏体积压裂水平井渗流模型，该模型既考虑了致密油藏双重介质渗流特点，又考虑了复杂缝网中裂缝倾角对油藏渗流的影响，以及裂缝相交后产量“劈分”流动。应用该模型识别出8种油藏渗流阶段，揭示了致密油藏体积压裂水平井渗流规律，并对关键性参数进行了敏感性分析。

1 物理模型描述

图1为致密油藏体积压裂水平井示意图，复杂缝网中，裂缝任意相交，共有16条裂缝。本文所建模型特征如下：1）致密油藏为上下封闭、无限大板状油藏，油藏渗流满足Warren等［14］提出的双重介质渗流特点。2）水平井在定产条件下开采。3）缝网中裂缝相互交叉形式包括2条裂缝相交（如图1中裂缝1，2）、Y字型裂缝交叉（如图1中裂缝5—7）、十字型裂缝交叉（如图1中裂缝2—5）以及多条裂缝交叉（如图1中裂缝9—14）。4）复杂缝网中所有裂缝均垂直穿透地层，裂缝内流体满足一维达西渗流。5）单相流体微可压缩，生产过程中油藏温度保持不变。6）忽略液体毛细管压力和重力的影响。

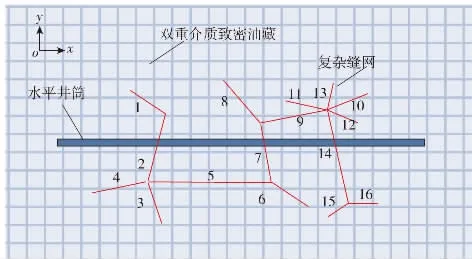
图1 致密油藏体积压裂水平井示意

2 数学模型建立

2.1 油藏渗流模型

致密油藏含有大量的天然裂缝，不能用常规的均质油藏模型进行描述。本文用双重介质模型来描述致密油藏（见图2）［14］，假设双重介质油藏由基质系统和天然裂缝系统组成。基质系统主要提供液体的储集空间，裂缝系统主要提供液体渗流通道。

图2 双重介质油藏示意

1991 年，Ozkan 等［9］在拉氏空间下建立了双重介质油藏面源函数，解决了双重介质油藏中分段压裂水平井的渗流问题。但Ozkan面源函数要求裂缝必须垂直或平行于水平井筒，不能解决复杂缝网中含大量倾斜裂缝的渗流问题。2017年，任宗孝等［13］在Ozkan面源函数基础上，建立了新面源函数，使之能解决倾斜裂缝渗流问题。单条倾斜裂缝渗流的拉氏空间解为

式中：p为压力，Pa；q为产量，m3/s；l为裂缝半长，m；K0为贝塞尔函数；s为拉氏变量；x，y为变量；θ为裂缝倾角，（°）；u为积分变量；下标f表示裂缝；下标D表示无因次变量；下标w表示井筒；“—”表示拉氏空间。

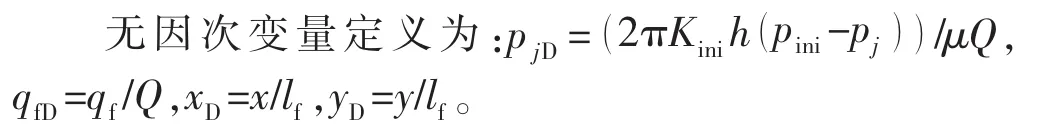
式中：h为地层厚度，m；Kini为渗透率，m2；pini为地层初始压力，Pa；pj为任意裂缝压力，Pa；qf，Q 分别为裂缝、油井产量，m3/s；μ为原油黏度，mPa·s。

考虑体积缝网内裂缝之间的相互干扰，由叠加原理［15］可知，任意一条裂缝的无因次压降fDi为

忽略裂缝的渗流阻力，则：

各裂缝无因次产量之和为1的限制要求为

将式（2）—（4）写成矩阵方程形式为

2.2 复杂缝网内渗流模型

2004 年国外学者 Karimi［16］应用“星-三角形”变换方法建立了复杂缝网内裂缝间传导率计算公式，多裂缝交叉裂缝间传导率计算通式为

式中：T为两裂缝之间的传导率，m3/（Pa·s）；K为人工裂缝渗透率，m2；D为两裂缝面心到交界面的距离，m；A为两裂缝的横截面积，m2；n为裂缝内法线单位向量；m为裂缝面心与交界面面心之间连线的单位向量。

基于裂缝间传导率，在一维达西渗流假设的前提下，首先给出Y字型交叉裂缝每条裂缝的产量公式：

式（9）即为含有3条裂缝的较为简单的复杂缝网渗流模型，同理可以写出Y字型、十字型及图1中复杂缝网渗流矩阵方程。由于图1中复杂缝网渗流矩阵方程太大，在此仅给出其矩阵向量形式：

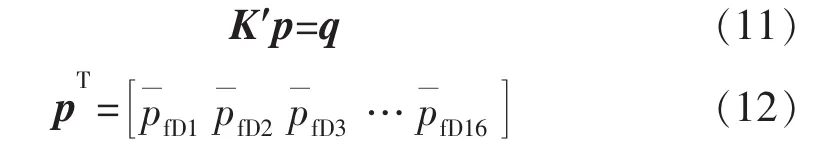
式中：K′为传导率矩阵 16×16阶。

2.3 半解析渗流耦合模型

忽略射孔孔眼压降以及水平井筒变质量管流压降，则裂缝2、裂缝7及裂缝14的压降相等，且等于井底压降。由定产生产的条件知，射孔孔眼流量之和为

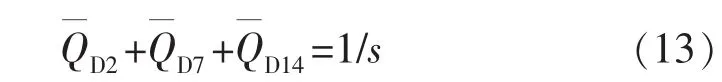
式中：QD2，QD7，QD14分别为裂缝 2、裂缝 7、裂缝 14 对应孔眼处液体流量，m3/s。

联立式（5）、式（11）、式（13），依据连续性条件（裂缝交界面处压力和流量相等），写出图1中致密油藏体积压裂水平井渗流矩阵方程：

式中：A为油藏渗流矩阵16×16阶；I为16×16阶单位矩阵；O为16×1阶0向量；Θ为1×16阶0向量。

其他向量具体表达式为

3 模型计算结果分析

3.1 致密油藏体积压裂水平井渗流阶段划分

为揭示致密油藏体积压裂水平井渗流规律，设计了一口简单的体积压裂水平井，缝网中裂缝纵横垂直交错。致密油藏基础参数见表1。

表1 致密油藏基础数据

在定产条件下求解体积压裂水平井的解。在双对数坐标系中作无因次压降pwD、无因次压降导数p′wD与无因次时间tD的双对数试井曲线（见图3）。

图3 致密油藏体积压裂水平井试井曲线

由图3可知，不同时间段无因次压降导数曲线显示的规律不同。结合前人对试井曲线的认识，可将体积压裂水平井划分为8个渗流阶段。

Ⅰ阶段为复杂裂缝内线性流。该阶段最早出现且持续时间很短，水平井产出的液体主要来自复杂裂缝内部。在双对数坐标系中，流动阶段Ⅰ的压降导数曲线斜率约为0.50。Ⅱ阶段为地层-裂缝双线性流。随着复杂缝网内液体的逐渐产出，压降波及到缝网附近的地层。地层内的液体线性流入裂缝，这时水平井的产液量一部分来自复杂缝网、一部分来自地层。在双对数坐标系中，该流动阶段压降导数曲线斜率约为0.25。Ⅲ阶段为地层线性流。地层中的流体线性流入裂缝，该流动阶段的压降导数曲线斜率约为0.50。Ⅳ阶段为过渡流。该阶段是地层线性流与缝网内裂缝间相互干扰流的过渡阶段。Ⅴ阶段缝网内裂缝间相互干扰流动。随着压降的进一步扩大，复杂缝网中的裂缝发生相互干扰，压降导数曲线出现“驼峰”状凸起。公开发表的文献中尚未有学者对“驼峰”状凸起进行研究。本文分析找出了影响该阶段渗流的主要因素。Ⅵ阶段为天然裂缝系统拟径向流。该阶段出现之前，水平井产出的液体全部来自天然裂缝系统。其主要反映了天然裂缝拟径向渗流特点。Ⅶ为窜流阶段，是双重介质油藏特有的渗流阶段，此阶段代表基质系统开始向天然裂缝系统供给液体。其主要特征是压降导数曲线有一“凹槽”，“凹槽”出现的早晚及持续时间的长短受窜流系数和储容比影响较大。Ⅷ阶段为整个油藏系统拟径向流。随着开采的持续进行，天然裂缝系统和基质系统都达到了拟稳态径向流，对应压降导数曲线为一水平线，且值为0.50［18］。

3.2 参数敏感性分析

3.2.1 缝网间距

致密油藏体积压裂水平井如图4所示，水平井中有2个纵横垂直交错缝网，缝网内共有24条裂缝。当两缝网间间距ΔL分别为200，500，1 000 m时，分析试井曲线的变化。

图4 致密油藏体积压裂水平井缝网示意

缝网间距主要影响流动阶段Ⅴ（复杂缝网间相互干扰），对其他流动阶段没有影响。随着缝网间距的增加，压降曲线以及压降导数曲线逐渐降低，“驼峰”状凸起也随之降低，说明缝网间相互干扰减弱。

3.2.2 体积缝网渗透率

假设复杂缝网中所有裂缝渗透率都相等，当裂缝渗透率分别为 108×10-3，107×10-3，106×10-3，105×10-3，104×10-3μm2时，分析试井曲线的变化。计算可知，缝网渗透率主要对前3个流动阶段影响较大。随着渗透率的逐渐增大，裂缝线性流以及双线性流持续时间越来越短。地层线性流持续时间越来越长，当裂缝渗透率增大到108×10-3μm2时，裂缝线性流以及双线性流消失。说明此时的裂缝渗透率极高，进入裂缝的液体几乎瞬间到达水平井筒。

3.2.3 压裂区体积

在缝网密度一定的情况下，为了分析压裂区体积大小对产能的影响，做了以下3组计算。3组计算中压裂区体积分别为 1.6×106，3.2×106，6.4×106m3。压裂区体积大小对水平井前5个渗流阶段影响较大，对后面的渗流影响较小。压裂区体积越大，无因次压降越小，说明相同产量下地层“能耗”越低；所以，在现场施工过程中应尽可能增加压裂区体积。

3.2.4 体积压裂区缝网形状

为了研究缝网形状对水平井生产的影响，对比了3种缝网（裂缝纵横垂直交错矩形缝网、裂缝纵横垂直交错椭圆形缝网，以及裂缝不规则分布的复杂缝网）的生产情况。在3组算例中人为设定，缝网的体积以及裂缝的总长度相等。计算可知，在压裂区体积和裂缝总长度相同的情况下，不同形状的缝网无因次试井曲线几乎完全重合。这说明在缝网规模一定的情况下，裂缝的形态对水平井生产几乎没有影响。