页岩气藏压裂水平井不稳定渗流模型及试井分析

雷宇 ，曾彦 ，宁正福

（1.北京石油机械有限公司，北京 102206；2.中国石油大学（北京）石油工程教育部重点实验室，北京 102249；3.中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249）

0 引言

我国各个地质历史时期的陆相及海相页岩中都有页岩气发育［1］。2013年，EIA估算我国页岩气可采资源量为31.6×1012m3，仅次于美国。截至2014年底，我国页岩气勘探开发累计投资230亿元，钻井780口（其中，直井 238 口，水平井 345 口）［2］，但我国页岩气开发目前仍处于摸索阶段。由于页岩储层不同于常规储层，具有多重储渗介质和多种流动形式特征，因此，常规的生产特征评价方法无法适应现场解释，需要根据页岩气的储层特征和气体流动特点，建立适应页岩气流动的评价分析方法。

为此，许多学者对页岩气藏压裂水平井的渗流理论开展了相关研究工作。Brown等［3］提出了一种简单的三线性流模型，假设在改造区之外的流动也是线性的且垂直于水平井筒，但该模型没有考虑页岩气的解吸和扩散特性。Moghadam等［4］利用天然裂缝系统的双重介质模型描述水力压裂创造的改造区域（SRV），该模型在SRV区域内能够有效地进行储层的动态分析和评价预测，但模型中并没有耦合微观扩散和吸附作用。Ozkan等［5］利用三线性流双重孔隙模型对比分析了毫达西级的常规砂岩储层和纳微达西级的非常规储层。苏玉亮等［6］针对体积压裂水平井的流动特征，提出了非常规储层体积压裂复合流动模型，依据体积压裂程度划分为4个流动区域，分别采用双重介质和均质介质描述不同区域的流动；但是，模型针对的是非常规油藏，而且没有考虑页岩气的微尺度特性。樊冬艳等［7］在传统的双孔单渗模型上，推导出了耦合吸附解吸的不稳定渗流模型，但该模型在基质分析过程中，只考虑了窜流项，并没有考虑基质中流体的渗流过程。谢维扬等［8］求解了页岩气多级压裂水平井非稳态渗流模型，在无因次产量递减图版上分析了解吸气和游离气对产量的影响。

综上所述，前人模型虽已能表征页岩气藏主要渗流特征，但往往不能综合考虑多重储渗介质和多种流动特征。本文基于非常规页岩气储层多尺度多流动空间的渗流特点，以线性流模型为主要依托，细化描述压裂体积改造区域和非改造区域，全面考虑储层内渗流、吸附和扩散作用，构建五线性流非稳态复合模型；利用Laplace变换和Stehfest数值反演解决数学问题，并通过与解析模型结果对比验证模型。该模型为提高产量和压力预测精度，以及为地质认识和工艺措施优化提供了依据。

1 页岩气藏渗流模型的建立

页岩气储层孔隙结构非常复杂，储层非均质性强，加上体积压裂改造，更加剧了储层的复杂性［9］：宏观尺度上，有水力压裂主裂缝到井筒的黏性流；微观尺度上，存在微裂缝内的黏性流和扩散流；纳观尺度上，存在基质表面吸附气解吸；分子尺度上，存在基质内孔隙扩散过程。由此可见，页岩储层具有很强的多尺度多流动空间的特性［10］。

在页岩气藏整个开发过程中，首先提供产能支持的是游离气，而其在页岩气生产周期的前几年会被大量采出。随着地层能量的损耗，压力的降低，开采出的游离气已不再是原始地层内的游离气，它是由原始游离气和解吸气组成的气流。解吸气通过扩散渗流过程从基质到微裂缝再到水力压裂主裂缝，经历解吸、扩散和达西渗流的过程到达井筒。因此，研究页岩储层多尺度多流动空间特征对产量有着深远的影响。

1.1 物理模型

实际地层中提及压裂改造的地层裂缝网络是十分复杂的。在2条水力压裂主裂缝之间存在由诱导缝和天然裂缝组成的缝网结构，压裂改造区之外是未压裂的致密页岩储层，这部分储层是页岩气长期（25～30 a）产量的保证［11］，不可以忽略。基于体积压裂改造区的构思，建立复合线性流数学模型。

根据页岩气藏渗透能力的大小将储层划分为5个区域［12-15］（见图1。其中，ye为2条人工裂缝间距离的半长，xe为x方向上贡献产量区域长度的半长，xf为双翼人工水力压裂裂缝长度，wf为水力压裂缝宽度，LⅣ为Ⅳ区在y方向上的长度）：Ⅰ区为水力压裂区；Ⅱ区和Ⅲ区为2条人工裂缝间区域，存在天然裂缝和诱导缝；Ⅳ区位于与Ⅱ区相连接的未压裂区域；Ⅴ区为与Ⅲ区相连接的未压裂区域。

图1 复合线性流物理模型

随着地层开始开采，压力首先在水力压裂主裂缝Ⅰ区产生响应，整个地层的产量都是由Ⅰ区供给到井筒的，因地层渗透性差异，Ⅱ区和Ⅲ区内压力响应要早于外围的Ⅳ区和Ⅴ区。Ⅰ区内流体流动方向主要是垂直指向井筒的x方向，Ⅱ区和Ⅲ区流动方向主要是平行井筒指向Ⅰ区方向，并且区域压力沿整个Ⅰ区均匀分布。随着地层压力进一步扩散，外围区域发生压力响应，Ⅳ区和Ⅴ区向Ⅱ区和Ⅲ区提供产量，其内流动方向为垂直指向井筒方向。整个流动区域存在2条设定的封闭边界：一条是2条水力压裂主裂缝中间区域，另一条是Ⅳ区和Ⅴ区外边界。

1.2 数学模型

本文采用双重介质模型来描述压裂后页岩气井渗流过程。针对双重介质，利用常规达西定律来描述裂缝中的流体运移，而基质中的流体运移机理采用解吸和扩散方法来描述［16］。

各类流动参数及无因次参数定义见表1。

表1 参数定义

1.2.1 Ⅴ区中的渗流

假设Ⅴ区为单重介质页岩储层。对达西渗透率进行修正，引入扩散效应和吸附解吸效应［17］，求得基质系统的控制方程：

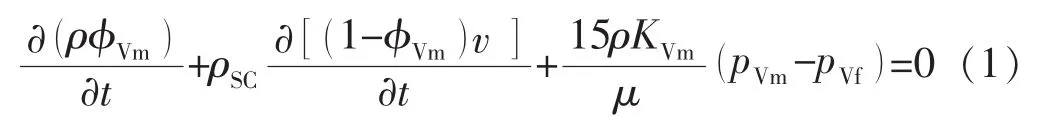
裂缝系统的控制方程为

根据表1，将式（1）和式（2）无因次化，并通过Laplace变换进行化简，可得：

将式（3）与式（4）联立，求得：

结合内边界与外边界条件，区域Ⅴ的数学模型可表示为

模型结果为

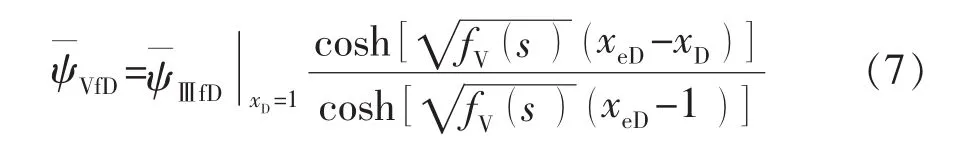
1.2.2 Ⅳ区中的渗流

与1.2.1中Ⅴ区的渗流一致，Ⅳ区的数学模型可表示为

1.2.3 Ⅲ区中的渗流

Ⅲ区的数学模型可表示为

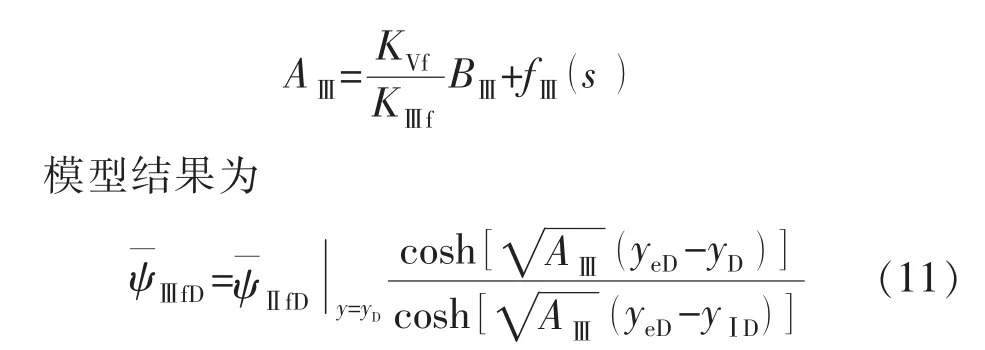
1.2.4 Ⅱ区中的渗流

Ⅱ区的数学模型可表示为

模型结果为

根据式（15），令xD=0，就可求得井筒压力。假设水平井井筒沿程无压降，则可求得井底拟压力：

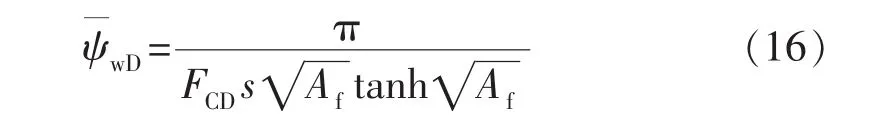
利用Duhamel原理，将井筒积液储集效应和表皮效应引入拟压力表达式：

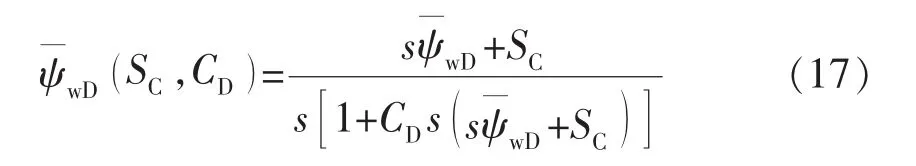
2 压力动态分析

模型结果为

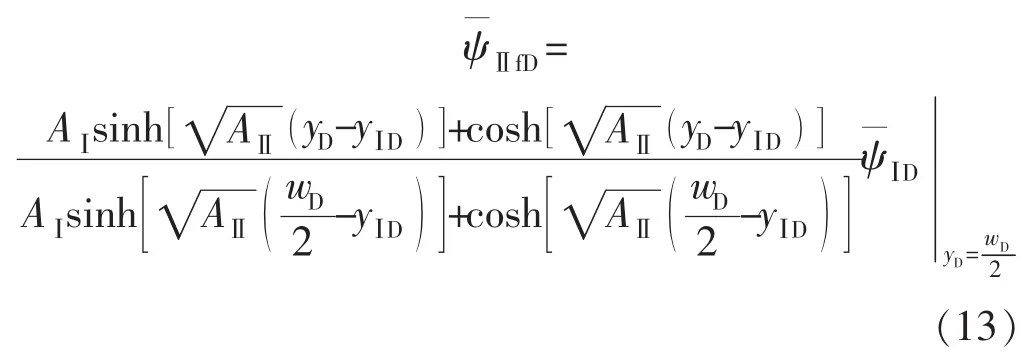
1.2.5 Ⅰ区中的渗流

Ⅰ区为压裂裂缝区域，其数学模型可表示为

2.1 流动区域划分

按照前文推导出的页岩气藏多级压裂水平井非稳态试井模型，结合实际井场数据，可以得到水平井无因次井底拟压力及拟压力导数随无因次时间变化曲线。针对体积压裂改造区非稳态渗流扩散过程，定义参数：ωⅡ=0.10，ωⅢ=0.08，λⅡ=0.50，λⅢ=1.0，xeD=3.0，yeD=2，y1D=1，wD=10-6，CD=10-4，SC=10-3。由压力动态曲线（见图2），可将流动状态划分为7个阶段：1）早期纯井筒储集阶段，压力线和压力导数线重合，并呈现45°，相比整个页岩气生命周期，这一阶段非常短暂［18］；2）过渡段，压力线与压力导数线分开，井筒储集效应影响减弱，表皮效应显著增强；3）水力压裂主裂缝与微裂缝的双线性流段，压力线和压力导数线斜率为0.25；4）微裂缝线性流段，压力导数线斜率为0.50；5）窜流段，体积压裂改造区的基质中，流体向裂缝发生非稳态窜流，鉴于非稳态窜流对压力比较敏感，因此不会出现明显的凹陷段；6）外部区域的综合线性流段，压力导数线斜率为0.50；7）封闭边界，两线重合，斜率为1.00。

2.2 弹性储容比的影响

弹性储容比是双重介质中描述储集能力大小的量，具体含义为裂缝储集与系统储集（裂缝储集能力+基质储集能力）能力的比值。分析Ⅱ区和Ⅲ区的弹性储容比对流态的影响，分别定义 ωⅡD=ωⅢD=0.1，0.3，0.5。从图3可以看出，弹性储容比影响了压力导数曲线凹陷的宽度和深度。弹性储容比与凹陷段持续时间、深度和宽度呈相反关系。当弹性储容比较小时，裂缝储集能力较弱，在相同的渗流能力下，流体在裂缝系统中流动持续时间较短。

图2 压力动态曲线

图3 弹性储容比对压力动态曲线的影响

2.3 窜流系数的影响

窜流系数表征了基质中的流体向裂缝供给的能力。分析Ⅱ区和Ⅲ区的窜流系数对流态的影响，分别定义 λⅡD=λⅢD=0.01，0.10，1.00（见图4）。

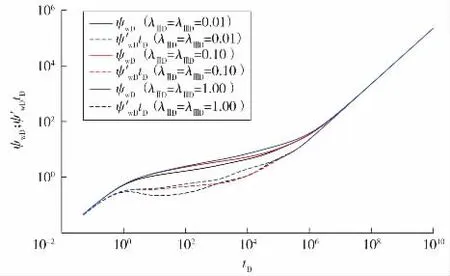
图4 窜流系数对压力动态曲线的影响

从图4可以看出，窜流系数对压力导数曲线凹陷段的深度和宽度影响不大，主要改变凹陷段的相对位置。窜流系数越大，基质流体窜流到裂缝的能力就越强，体现在压力导数线上则是过渡段越靠前，同时裂缝系统流态过程减短；随着窜流系数的增加，发生在裂缝中的流态（线性流，双线性流）类型越来越少，甚至会被下凹段掩盖。

2.4 吸附因子的影响

吸附因子表征的是自由气和解吸气的相对关系。分析储层吸附因子对流态的影响，分别定义αⅡD=αⅢD=αⅣD=αⅤD=0.1，0.3，0.6。从图5 可以看出，改变吸附因子对气井后期流态影响较大。吸附因子越大，解吸量越少。随着吸附因子的增大，压力导数曲线下凹段宽度和深度不断减小，同时系统进入拟稳态流态的时间提前。这是由于，吸附因子越大，说明储层中蕴含的吸附气越多，进而能够从基质中解吸附并扩散至天然裂缝的页岩气也越多。更多的吸附气来补充地层压降，使得压力曲线上升［15］。

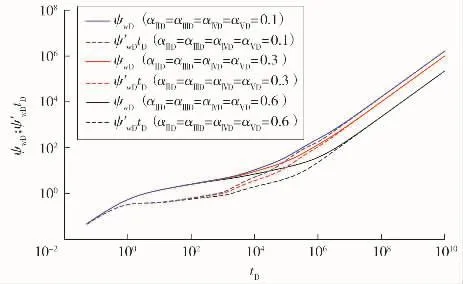
图5 吸附因子对压力动态曲线的影响

3 实例分析

H1页岩气井位于威远构造东翼轴部，威远背斜位于乐山-龙女寺加里东古隆起的西南部，长轴92.0 km，短轴30.8 km。构造北翼地层较缓，目的层位是龙马溪下段，中深1 550 m。该井于2011年1月开钻，设计生产制度为控压生产，设计水平段长度1 080 m，水力造段段数11级，测试产量为1.34×104m3/d。

H1井压力恢复试井：压力计测深约1 300 m，关井进行压力恢复前平均套压2.84 MPa，平均油压0.94 MPa，气量在1.14×104m3/d左右，按照方案回压15 d，进行测试。关井最高套压9.85 MPa，最高油压9.85 MPa。基础参数为：储层厚度70 m，孔隙度3.97%，温度74.34°C，压力 10.98 MPa，压缩因子 0.916，黏度 0.015 3 mPa·s，压缩系数 0.141 MPa-1。

将实际试井数据按照气体的特性处理后，利用本文建立的五线性流非稳态复合模型进行拟合分析（见图6）。从双对数拟合图像上看，采用窗口求导方法得到的数据波动相比两点差分方法有所改善，拟合精度也较高。从该井生产历史看，本次试井解释前，该井经过了很长一段生产时间，压力下降幅度较大，试井分析压力起始点较低，前期的压力导数出现负斜率，反映出了很严重的井底积液情况［19］。由于井筒储集段并不是本研究的重点，所以模型分析从前期的线性流开始。由拟合图形可以看出，经过过渡段后出现了短暂的线性流段，紧接着就是早期的径向流段。

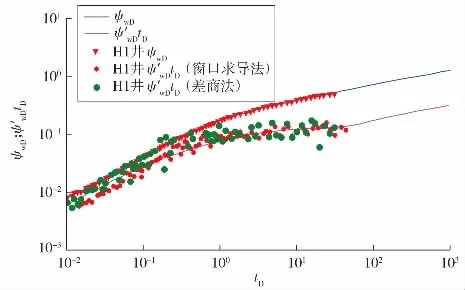
图6 H1井压力双对数拟合

将本文模型解释结果与刘晓旭等［13］的模型解释结果进行对比（见表2）。

表2 模型结果对比

对比结果比较理想，本文模型拟合结果具有一定可靠性。约为10 m的裂缝半长远小于地震监测与施工设计，它反映的是一个有效的裂缝半长概念，受控于水力压裂主裂缝的渗透率，无法反映出微裂缝和诱导缝的影响。同时，可以看出页岩储层在没有经过压裂改造之前，渗透性极差（0.000 87×10-3μm2），水力压裂在一定程度上极大地改善了井筒附近的渗透能力。

4 结论

1）页岩储层微观孔隙、裂缝和水力压裂缝中存在的吸附、扩散和渗流特征使其有别于常规气藏储层。页岩储层开发动态分析必须要综合考虑这些特征，才能较为准确地贴近页岩真实的生产过程。

2）弹性储容比和窜流系数综合作用于基质向裂缝的过渡段形态，且拟稳态模型比非稳态模型更加明显。无因次压缩系数控制自由气和吸附气含量，其值越大，释放吸附气越少，吸附气对产量的贡献越少。

3）模型中，无因次压缩系数是吸附气供给能力的表征，其值越大，吸附气供给就越少，系统到达拟稳态时间就越早；无因次弹性储容比越小，凹陷段存在越久，深度加大，裂缝储集能力相对较弱，流体在裂缝系统流动持续时间就越短；无因次窜流系数增大，过渡段起始点更加靠前，同时裂缝流态存在时间受到影响。

5 符号注释

ψ为拟压力，MPa2/（mPa·s）；μ为气体黏度，mPa·s；Z为气体压缩系数；p为储层压力，MPa（p′同 p，作为积分变量区别于 p）；pini为初始压力，MPa；ωi为第 i区储容比；φif，φim分别为第i区天然裂缝和基质的孔隙度；Cif，Cim分别为第i区天然裂缝和基质的综合压缩系数，MPa-1；λi为第 i区窜流系数；αi为第 i区吸附因子；Kim，Kif分别为第i区基质和天然裂缝的渗透率，10-3μm2；R为基质块半径，m；ηi为第 i区导压系数，m2/h ；ψD为无因次拟压力；hⅡ为Ⅱ区储层厚度，m；qsc为气井产量，m3/d；T为储层温度，K；ψi为初始拟压力，MPa2/（mPa·s）；ρSC，ρ分别为标况和地层条件下的气体密度，kg/m3；VL为 Langmuir体积，m3/kg；pL为 Langmuir压力，MPa；ψD为无因次拟压力；hⅡ为Ⅱ区储层厚度，m；qSC为气井产量，m3/d；t为生产时间，h；ηiD为第 i区无因次导压系数；xD，yD分别为x方向和y方向无因次坐标，m；x，y分别为x方向和y方向坐标，m；Kiam为第i区基质视渗透率，10-3μm2；pim为第 i区基质压力，MPa；pif为第 i区裂缝压力，MPa；s为拉普拉斯变量；imD为第 i区基质无因次拟压力；ifD为第i区裂缝无因次拟压力；v为气体渗流速度，m/s；y1D为压裂裂缝到渗透边界的无因次距离（可表示为y1D=y1/xf）；y1为压裂裂缝到渗透边界的距离，m；wD为无因次压裂裂缝宽度（可表示为 wD=wf/xf）；wf为压裂裂缝宽度，m；CD为无因次井筒储集系数；SC为表皮因子；下标 i=Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ；下标Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ分别代表Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ区；下标D代表无因次；下标f，F，m分别代表天然裂缝、压裂裂缝系统和基质系统；下标w代表井眼；下标e代表裂缝距离储层边界的长度。