朝阳沟油田扶余油层组深度域地质统计学反演

陈旭辉

（中国石油大庆油田有限责任公司勘探开发研究院，黑龙江 大庆 163712）

1 问题的提出

大庆朝阳沟油田位于松辽盆地中央坳陷东部朝阳沟阶地及长春岭的背斜上，其主要开发层系是扶余油层组，该油层组属于白垩系泉头组的泉三段中上部以及泉四段。该套地层的顶界面埋深500～1 500 m，地层厚度210～240 m，发育薄互层砂体，且横向变化快，物性较差，属于典型的低孔隙、低渗透性储层，开采与预测难度都较大。常规时间域地质统计学反演预测方法虽然在纵向上对砂体的识别能力较高，但其一个显著的缺点是与构造匹配能力有限，对砂体空间展布形态及砂体边界的精确描述仍存在一定的缺陷，其预测精度难以满足实际生产的需求，尤其是在指导水平井实施过程中，这一缺陷尤为突出，大大增加了钻井风险。因此，有必要寻找一种更高精度与更强实用性的反演预测方法［1-7］。

2 深度域地质统计学反演方法

深度域地质统计学反演方法，主要包括速度模型的建立、构造模型的建立和深度域地质统计学反演3个部分。

2.1 速度模型的建立

深度域反演一个较为重要的参数模型就是速度模型。由于深度反演所依托的地震剖面仍为时间域剖面，因此速度模型的建立显得尤为重要。在这里仅建立目的层段的速度模型。

2.1.1 速度模型的实现流程

为确保模型的精度，在此采用较为精确的叠前时间偏移均方根速度谱，利用速度约束技术（CVI），结合人工神经网络BP算法，使速度场收敛与平滑；再通过式（1）变换，将均方根速度转为时间域的层速度［8-9］；应用层析迭代技术，建立更高精度的层速度模型；最后在实钻井速度低频趋势模型、地震解释层位与层析速度模型共同约束下，再次采用速度约束技术，对速度谱进行内插平滑。层速度变换公式为

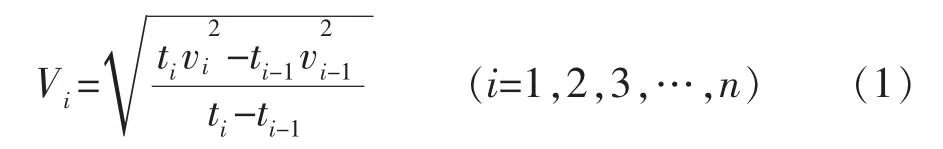
式中：Vi为第i层的速度；vi，vi-1分别为第 i层和第 i-1层的均方根速度；ti，ti-1分别为第i层和i-1层的时间。

通过对时间域的层速度进行时间深度转换，就可得到一个精度较高且较为平滑的速度模型（见图1）。该速度模型较叠加速度谱有着更高的精度与平滑度，其横向趋势变化符合地质构造规律。

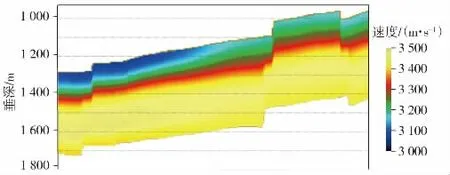
图1 深度域速度模型

2.1.2 人工神经网络BP算法

David等人提出的误差反向传播（BP）算法，由正向传播数据流与反向传播误差数据流2个学习过程组成。在传播过程中，通过调整各个输入参数神经元的权限值系数来控制期望输出模型与实际模型的误差最小，最终达到收敛的模型输出［10-12］。

BP训练算法流程：

1)初始化产生随机的权向量，设定步长参数与结束条件等。2）对输入数据流计算隐含与输入、输出数据数据流。3）由期望输出与上一步的实际输出计算目标函数的误差值总和。4）对计算权值进行修正。5）判断结束条件，满足则记录权值并输出最终模型，不满足则到第2步。

BP神经算法计算公式：

式中：up为输入数据流；p为各神经元；i为样本点；wi为神经元权值；vi为输出数据流。

目标函数为

式中：E为误差总能量值；ys（p）为期望输出模型；yf（p）为实际输出模型。

2.2 构造模型的建立

在构造模型的建立当中，构造图的制作尤为重要，其精度直接影响到储层反演结果与后期井位部署的效果。这里着重介绍构造变化简单与地层厚度横向变化小的高精度构造图制作方法。本工区共解释了T2，F21，F31，Y11共4个层界面。其中：T2相当于扶余油层的顶界面；F21相当于扶二油层组的顶界面，可划分出FⅠ1—FⅠ7共7个小层；F31相当于扶三油层组的顶界面，与上覆层间可划分出FⅡ1—FⅡ5共5个小层；Y11相当于扶余油层的底界面，与上覆层间可划分出FⅢ1—FⅢ5共5个小层。构造模型的建立就是要把所有的17个小层搭建完毕。

2.2.1 构造图制作步骤

以扶余顶界面的构造图制作为例。通过前述的速度模型对等T0图进行时间深度转换，转换前后构造图见图2a，2b。转换后的构造图与实钻井地质分层仍有存在着一定的误差，需要进一步校正。采用实钻井地质分层与预测构造面的误差趋势面法进行校正，校正后误差小于1 m（见图2c），满足后期的反演需求。

图2 构造图制作过程

依照上述方法分别制作出扶二顶、扶三顶与扶余底构造图。

2.2.2 构造模型的制作

在保证构造界面精度较高的情况下，通过上下层间趋势控制与井点分层的外推内插，生成小层构造界面。小层的内插算法采用经验贝叶斯克里金算法薄板样条函数模型（EBK）：

式中：Nugget为块金值；h为距离；b为坡度。

内插得到的各小层界面与实钻井地质分层吻合度高，未见异常值，构造趋势符合界面走势，结合断层的搭、切关系制作构造模型（见图3）。

图3 研究区构造模型

2.3 深度域地质统计学反演

深度域地质统计学算法，采用非线性最小平方目标函数来实现［13-17］。该算法在贝叶斯模糊判别基础上，利用井点输入的全体样本数据，纵向上采用马尔科夫链蒙特卡洛模拟（MCMC），横向上采用多网格蒙特卡洛模拟算法（MGMC），将传统地质统计学的高斯随机空间概率分布与非线性最优化求解的迭代过程进行整合。在稀疏反射系数地质模型的基础上，通过贝叶斯模糊识别进行循环迭代，是一种以误差的平方和为最小准则来估计非线性静态参数的一种参数估计方法［10］。

非线性系统的模型为

式中：y为系统的输出；x为输入；θ为参数。

这里非线性是指对参数θ的非线性模型。则估算参数的目标函数为

非线性最小二乘法就是求使Q达到极小的参数估计值，此时模型停止迭代，输出最终模型参数。

图5为本研究区的反演效果图。其中，暖色调为高概率砂岩发育区，测井曲线为自然伽马，曲线值向右增大。从过井的反演剖面可以看出，反演结果与实钻井吻合很好，可以分辨出2 m以下的薄砂层，横向趋势过渡自然，无“扫帚”状等奇异区出现（见图4）。

图4 深度域过井反演剖面

3 应用效果分析

应用本文研究成果，在FⅠ7号小层，设计了一口水平井，参照FⅠ7小层单砂体厚度预测图（见图5），设计水平段长度1 500 m，实钻1 684 m。图6为过设计井砂岩预测剖面，黑色线段为水平井轨迹，方向为北东—南西。从图6可以看出，预测的砂岩条带性非常明显，边界清晰，结合该区的地质特征以及邻近井地质特征，综合判断该条带应为河道砂岩。

图6 水平井过井剖面

从实钻的效果来看，砂岩钻遇率为94.2%，钻遇砂岩段油气显示段长度为1 434 m，占水平段总长度的85.1%，占钻遇砂岩段的90.3%，吻合精度很高（见图6）。从水平井过井剖面来看，剖面中红色箭头标记出的泥岩区域，与砂岩平面预测图件中对应位置的砂岩不发育区域也是吻合的。整体上看，预测成果与实钻效果吻合程度较高。

4 结论

1）速度模型与构造模型对后期的反演效果影响较大，因此反演成功的关键是保证模型的精度。

2）对构造复杂区域，该方法也同样适用。构造图制作要精细，地震解释要细致，尤其要落实微幅度构造与小断层的展布特征。

3）深度域地质统计学反演方法很好地将反演结果与构造特征进行了整合，相较于时间域反演更适用于地质研究。

4）反演算法异常复杂，针对不同地区、不同地质特征与地质任务，应采用适合的算法，不可一概而论。