基于Kameda模型的爆炸地震动时变功率谱拟合

陈辉国，宋 浩，钟 庭，刘国粹，王苗硕

(1. 陆军勤务学院 军事设施系，重庆 401331; 2. 69056部队，新疆 乌鲁木齐 830000)

0 引 言

在工程中，为了研究爆炸震动对结构的影响，需要将其震动记录作为结构的动力输入来进行计算分析。但由于真实记录的有限以及不能很好的符合所需场地特性，常常需要人工合成爆炸地震波。由于人们对于天然地震波已经有了比较充分的研究，因而根据天然地震波与爆炸地震波之间的联系，可以参照人工合成地震波的方法来研究爆炸地震波的模拟。目前在人工地震波合成领域常用的方法主要有两类[1]：一类是地震学方法，即基于震源过程分析和格林函数计算两个部分进行地面运动研究，考虑断层破裂产生的条件、过程以及非均匀介质的吸收对传播造成的影响；另一类是工程方法，即基于地震动参数统计关系和随机过程理论，注重实际地震动参数诸如幅值、持时、频谱等，使用数学方法对加速度时程的细节进行刻画，其中应用最为广泛的是随机过程方法，通常分为平稳随机过程、强度非平稳的随机过程以及强度和频率都非平稳的随机过程。对于爆炸地震动拟合，目前研究人员提出的非平稳随机过程主要是强度非平稳模型，最为常用的是由一个零均值平稳随机过程与幅值包络线函数的乘积来实现其强度非平稳，如曾德斌等[2]经过研究改进M. SHINOZUKA等[3]得出的双指数包络函数后应用于爆炸地震波的模拟，国胜兵等[4]指出林大超基于阻尼半空间爆炸点源加载模型改进幅值包络和功率谱函数式进而模拟能够考虑装药量和爆距影响的爆炸地震波时程，这些方法虽然在一定程度上体现了爆炸震动的强度非平稳特性，但是频率非平稳特性并没有得以体现。林大超等[5]研究表明，爆炸震动的时频非平稳特性是其一个重要属性，在自然地震研究方面，已有大量学者对地震动的时频非平稳模拟进行了研究，主要有短时傅立叶变换，小波变换，HHT等，其中 H. KAMEDA，M. SUGITO等[6-8]提出采用时变功率谱和随机相位谱来实现地震动的时频非平稳，该方法简便，具有很好的工程适用性，但由于其是基于日本强震记录得出的公式、衰减规律，故需要进一步研究其是否适用于爆炸震动的模拟。笔者根据爆炸地震动时变功率谱的特性变化规律，在H. KAMEDA，M. SUGITO等研究的基础上，采用Kameda时变功率谱进行爆炸地震动拟合，并选取实际爆炸震动记录进行了验证分析，从而通过时变功率谱模型实现时频非平稳爆炸地震动的拟合。

1 Kameda时变功率谱模型

1.1 多重滤波技术计算时变功率谱

Kameda提出采用多重滤波技术计算强地面运动加速度时程的时变功率谱，求出诸多不同频率的单质点振子在给定输入运动下的输出反应。单质点体系受基底x(t)激励下的运动方程为

y″(t)+2ζωy′(t)+ω2y(t)=-x(t)

(1)

式中：y(t)、y′(t)、y″(t)分别为相对位移、相对速度和相对加速度反应时程；ζ为阻尼比，在中小强度的地震时，一般取ζ=5%；ω为振子的圆频率；x(t)为输入加速度时程。

如果用与振子总能量有关的函数R(t,ω)来表示振子的随机反应，则可得

R2(t,ω)=y2(t,ω)+y′2(t,ω)/ω2

(2)

对式(2)取集合平均得

ER2(t,ω)=Ey2(t,ω)+Ey′2(t,ω)/ω2

(3)

因为

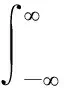
(4)

式中：y(t,ω)为t时刻ω频率点的相对位移反应时程；H(ω)为振子的位移传递函数；Sx(t,ω)为输入加速度时程x(t)为t时刻ω频率点的时变功率谱。

当时变功率谱Sx(t,ω)比传递函数|H(ω)|2平滑时，则可近似得到

(5)

(6)

将式(5)和式(6)代入式(3)，并且Sx(t,ω)=Gx(t,ω)/2，得到时变功率谱的近似公式：

(7)

式中：Gx(t,ω)为输入x(t)的时变功率谱；y(t,ω)、y′(t,ω)分别为t时刻ω频率点的相对位移、速度反应时程。

根据上述公式，首先计算各个频率点的相对位移、相对速度反应时程，再代入式(7)即可得到对应频率点的时变功率谱。但是需要注意的是，由于谱的随机特性的影响，通过上述方法得到的时变功率谱图形波动比较大，故需要对其进行平滑处理。可选用Parzen窗函数[9]对时变功率谱值进行平滑处理：

(8)

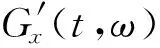
1.2 Kameda时变功率谱模型及参数确定

Kameda使用前述的多重滤波技术计算日本84个地震加速度时程的时变功率谱，通过统计分析研究提出其表达式：

t>ts

(9)

式中：Gx(t,2πf)为该模型的时变功率谱；f=ω/2π；αm(f)为时变功率谱模型峰值的平方根；ts(f)为f频率点时变功率谱起始时间点，通常取Gx(t,2πf)=0.1Gmax(t,2πf)对应的t值，其中Gmax(t,2πf)为实际地震动时变功率谱的峰值；tp(f)为时变功率谱起始时间点ts(f)到峰值的持时。对于各参数的具体含义，详见图1。

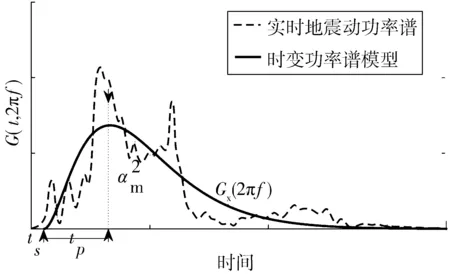
图1 实际地震动功率谱与时变功率谱模型示意Fig. 1 Recorded and simulated evolutionary power spectra

M. SUGITO等[7]通过分析日本118条实际地震动记录的时变功率谱，统计其衰减规律，式(9)中各参数随频率的参数化模型表达式为

lgαm(f)=a1+a2lgf+a3(lgf)2

(10)

lgtp(f)=b1+b2lgf+b3(lgf)2

(11)

(12)

式中：tm为所有离散点处ts(f)的均值，a1、a2、a3、b1、b2、b3、c1、c2、c3为系数。

2 实例分析

2.1 爆炸记录的选用

为分析Kameda时变功率谱模型的有效性，选取重庆市轨道交通一号线工程大坪—石油路区间地下爆破施工时测得的爆炸震动加速度时程曲线进行分析，爆破采用二号岩石硝铵炸药，密度0.85～1.05 g/m3，药卷直径φ32 mm，图2为右线3号测点的爆炸地震动加速度时程曲线。

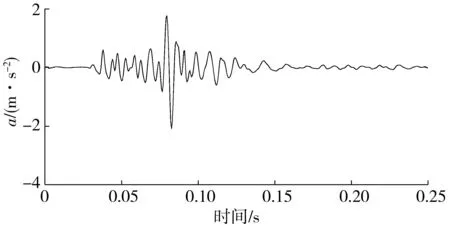
图2 爆炸加速度时程Fig. 2 Time history of explosive acceleration

2.2 Kameda模型参数识别

使用Kameda时变功率谱模型，钟菊芳等[10]提出取低频截止频率为f=0.125 Hz，同时考虑到大多数建筑物的频率范围为0.1～10 Hz，则频率点的范围取定为0.125～10.125 Hz，频率间隔Δf=0.20 Hz；使用Parzen窗函数对时变功率谱进行平滑时，取等效带宽b=0.1π rad/s。使用该模型计算各频率点的时变功率谱，并利用最小二乘法拟合该爆炸记录对应51个频率点αm(f)、ts(f)、tp(f)参数值，其中前9个频率点的时变功率谱拟合结果如图3，从图3中可以看出使用Kameda模型拟合结果能够较好的反映计算值的主体特征，拟合效果良好。

图3 时变功率谱随时间变化图(图中的频率点范围为0.125～1.175 Hz)Fig. 3 Variation of evolutionary power spectra changing with time (the range of frequency points in the figure is 0.125～1.175 Hz)

2.3 模型参数随频率变化拟合

采用式(10)～式(12)对51个频率点进行时变功率谱模型参数拟合之后，得到各个频率点下的参数取值，参数值的表达式中各个系数值如表1，将参数随频率的变化统计并拟合，各参数拟合执行水平情况见表2，拟合结果如图4，从图4中可以看出αm随频率的增加先增大后减小，ts随频率的增加先增大后减小，tp随频率的增加而增大。

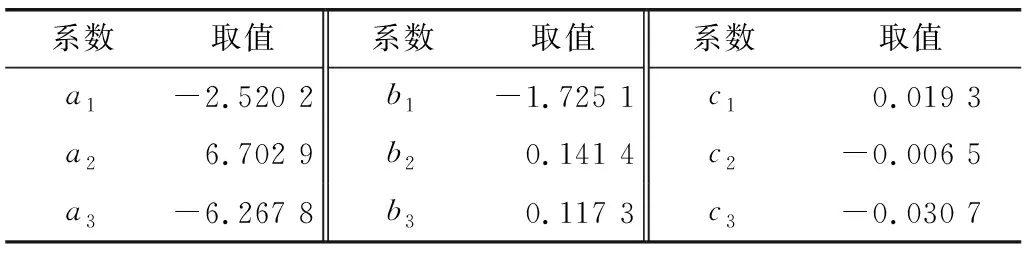
表1 式(10)～式(12)中各系数的取值Table 1 Value of each coefficient of the formula (10) ～ (12)

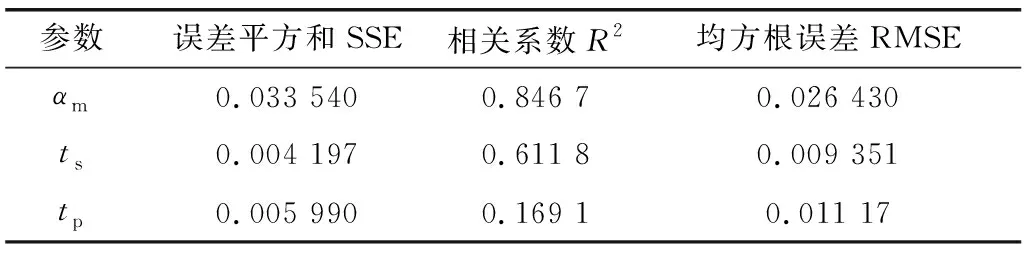
表2 各参数拟合执行水平Table 2 The performance level of the fitting of each parameter

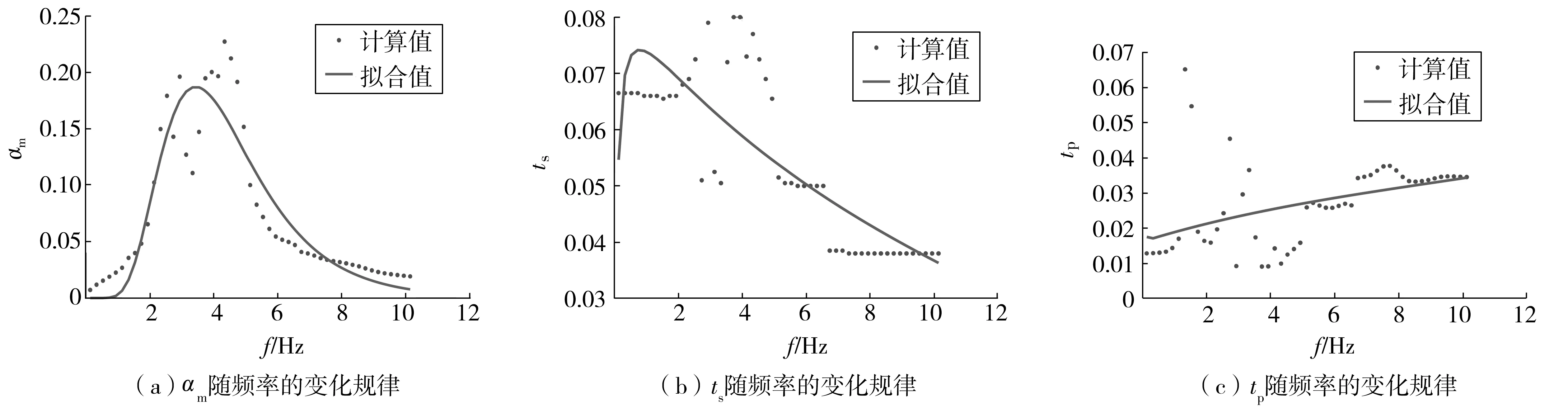
图4 αm、ts、tp随频率的变化规律Fig. 4 The variation rule of αm、ts、tp changing with the frequency

2.4 时变功率谱比较

为比较模型化后的时变功率谱与原始爆炸地震动的时变功率谱的近似程度，图5分析给出了由多重滤波技术得到的真实爆炸记录的近似时变功率谱〔图5(a)〕，根据时变功率谱模型参数计算值得到的拟合时变功率谱〔图5(b)〕，以及根据时变功率谱模型参数拟合值得到的时变功率谱〔图5(c)〕，从图5中可以看出模型化后的时变功率谱与实际的时变功率谱有较高的一致性，由模型参数计算值得到的时变功率谱与实际的时变功率谱有更高的一致性，模型参数拟合值的时变功率谱是平滑后的计算值的时变功率谱，主体特征保留，与实际时变功率谱也有较高的一致性。

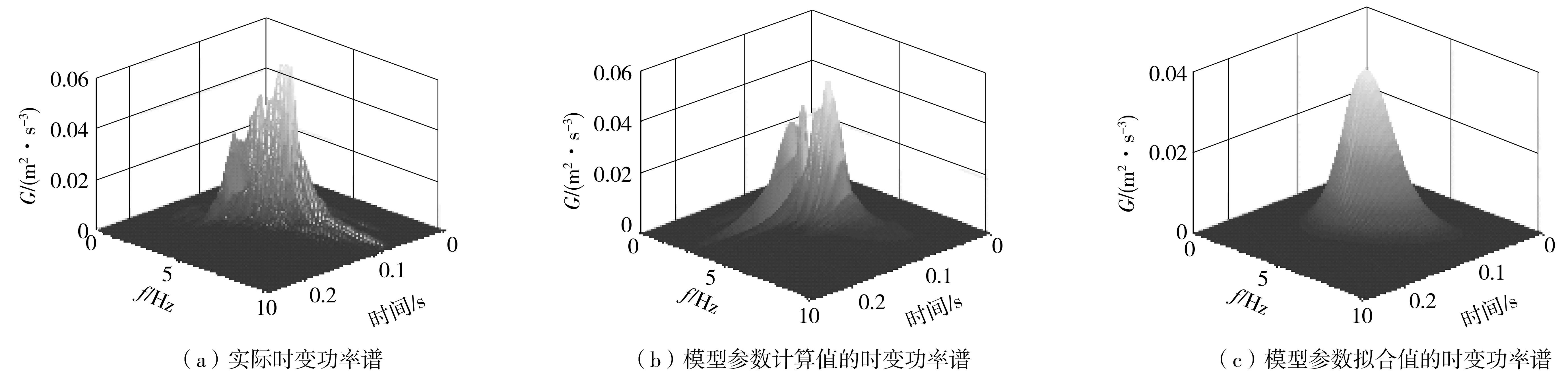
图5 实际与模型时变功率谱比较Fig. 5 Comparison of the recorded and simulated evolutionary power spectra

2.5 爆炸地震动合成

按照M. SHINOZUKA等[3]提出的非平稳时程模拟方法，基于时变功率谱模型可按下式进行爆炸地震动合成：

(13)

式中：x(t)为合成的加速度时程；G(t,2πfk)为t时刻2πfk频率点的时变功率谱值；Δf为频率间隔；φk为(0,2π)内均匀分布的随机相位角。

由时变功率谱合成时程曲线时，考虑两种情况：①根据模型参数计算值得到的时变功率谱〔图5(b)〕合成的爆炸时程曲线〔图6(a)〕；②根据模型参数拟合值得到的时变功率谱(图5(c))合成的爆炸时程曲线〔图6(b)〕，拟合的加速度时程曲线如图6。

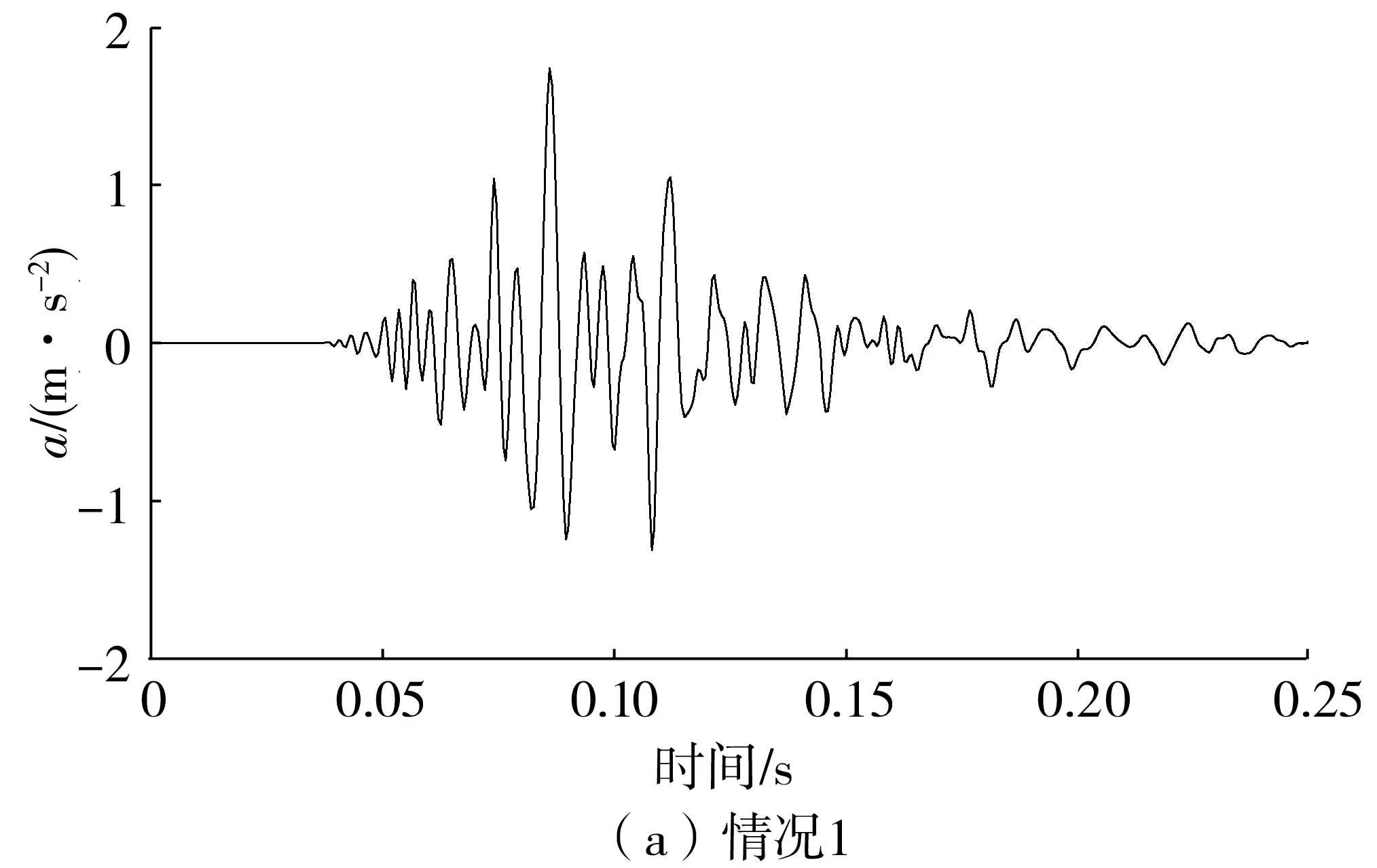
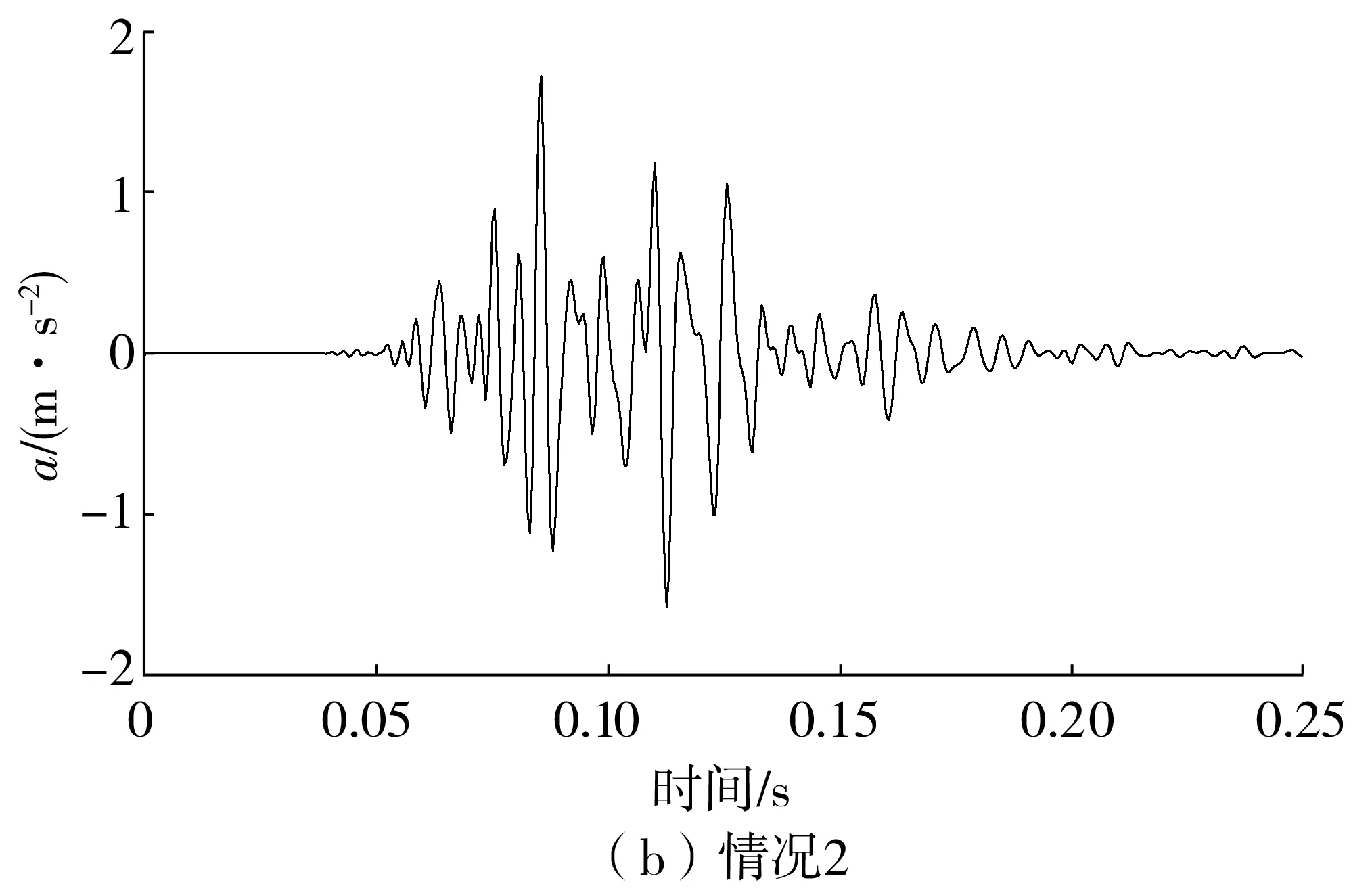
图6 合成的加速度时程曲线Fig. 6 Time history curve of the artificial acceleration

图7分别给出了两种情况下的拟合时程与记录时程的反应谱比较：①图6(a)与记录的加速度时程反应谱比较；②图6(b)与记录的加速度时程反应谱比较，从图7中可以看出拟合与记录的加速度反应谱曲线有较高的一致性，情况2的加速度时程反应谱尽管与实际的出入较大，但大体符合实际的特征，有较好的一致性。

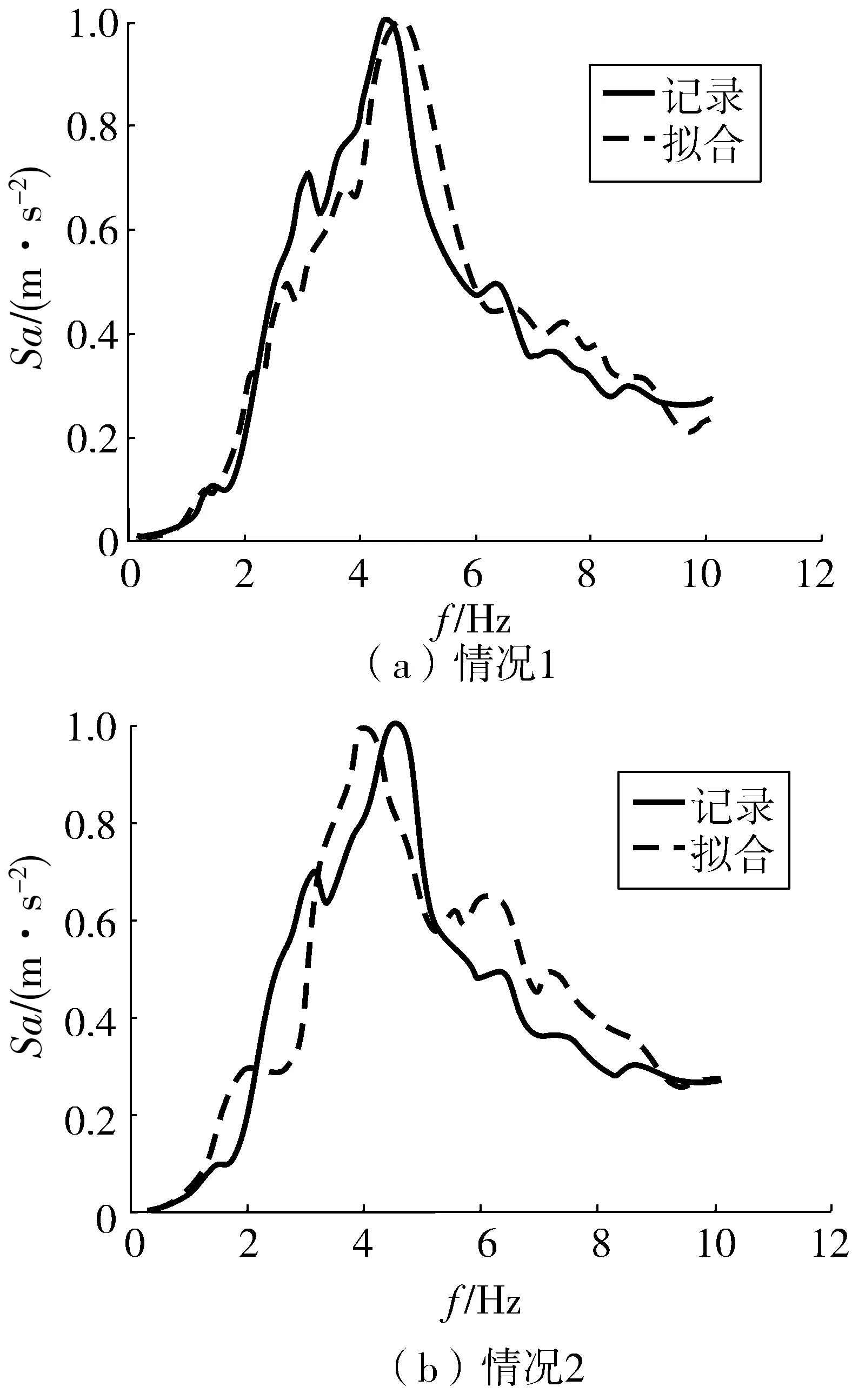
图7 记录与合成加速度反应谱比较Fig. 7 Comparison of response spectra for the recorded and the artificial acceleration

为比较拟合爆炸地震动与原始爆炸地震动的时域非平稳性，图8给出了原始爆炸时程、情况1的拟合爆炸时程图6(a)、情况2的拟合爆炸时程图6(b)的强度包线，可以看出原始爆炸地震动与拟合爆炸地震动强度非平稳特性也非常接近。

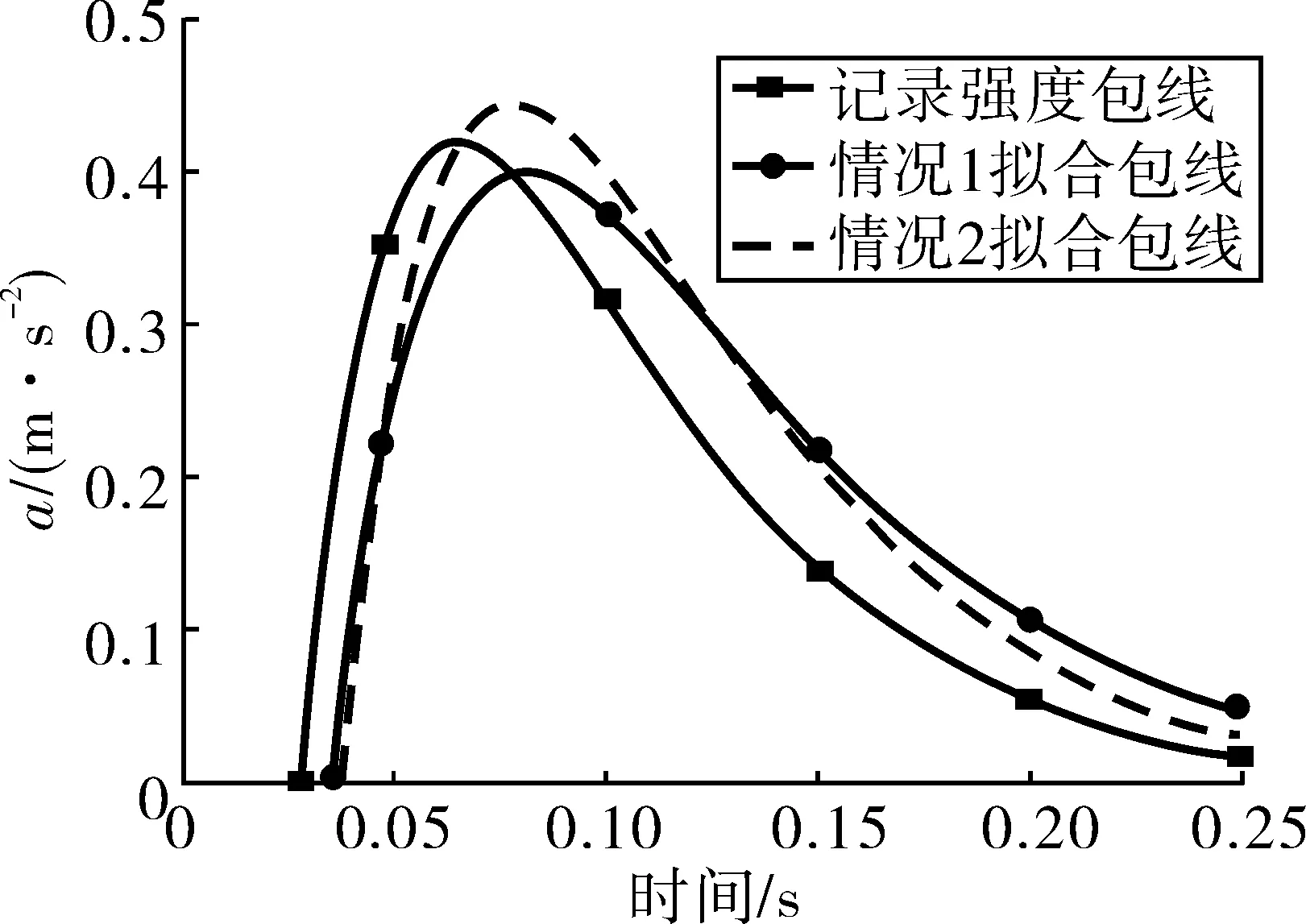
图8 记录与合成加速度强度包线比较Fig. 8 Comparison of the intensity envelope of the recorded and the artificial acceleration

根据G. R. SARAGONI等[11]的研究成果，穿零率对反映地震动的频率非平稳性具有非常重要的指导意义，为此，比较拟合爆炸地震动与原始爆炸地震动频率非平稳性，图9分别给出了两种情况下的累积穿零次数比较：①图6(a)与原记录时程的累积穿零次数比较；②图6(b)与原记录时程的累积穿零次数比较。

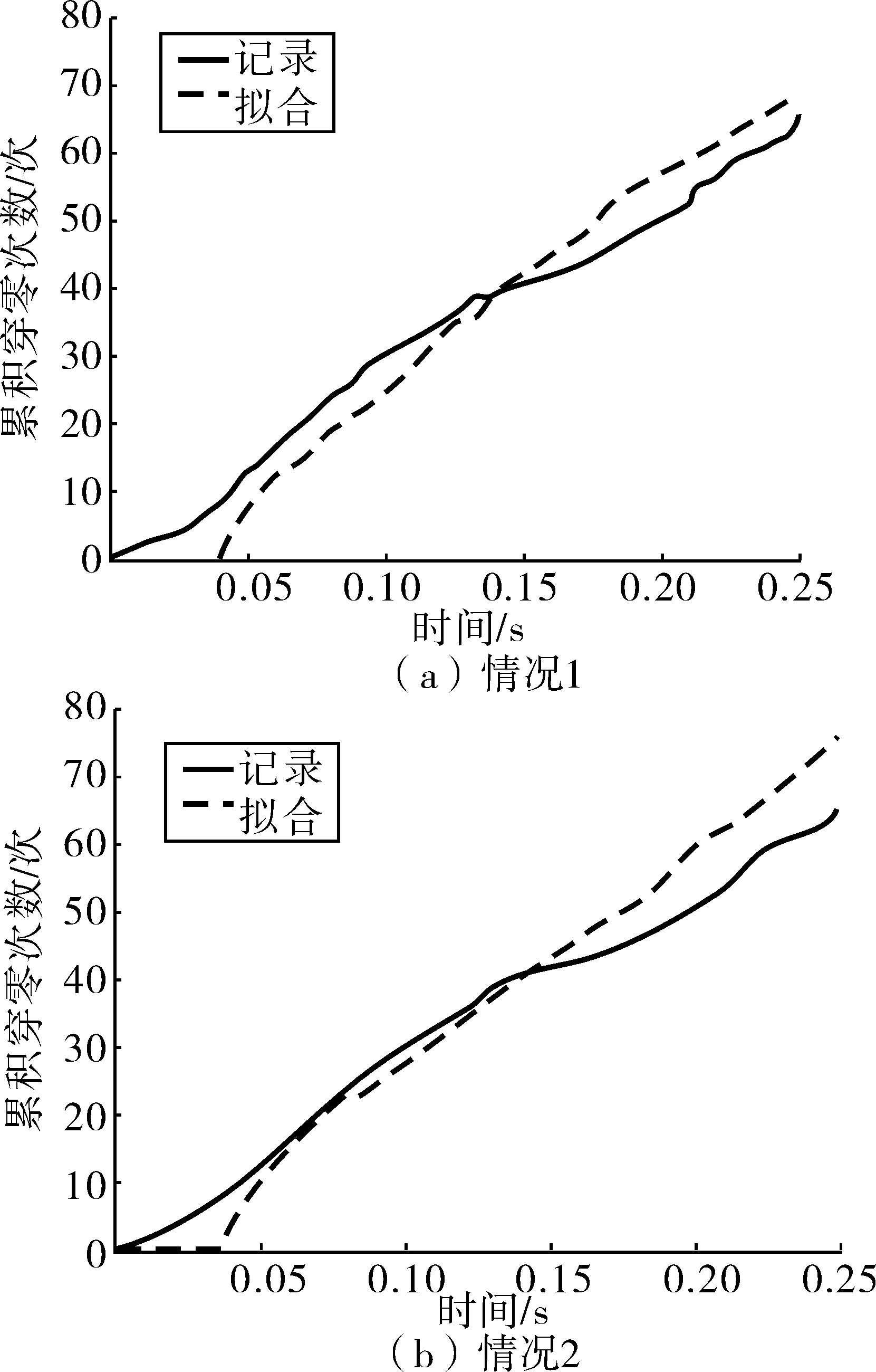
图9 记录与合成加速度累积穿零次数比较Fig. 9 Comparison of cumulative times of zero-crossing of the recorded and the artificial acceleration

从图9中看出拟合时程与记录时程都表现出频率非平稳性，情况2的误差相对大一些，但仍能大体反映出原始记录的特征。

通过比较记录与合成加速度时程(图2，图6)，以及记录与合成加速度反应谱(图7)、强度包线(图8)、累积穿零次数(图9)，可以发现通过此方法合成的爆炸加速度时程与记录时程可以保持较高的一致性，并且可以实现时域和频域均非平稳的爆炸地震动加速度时程的合成，由此说明该方法是可行的。通过模型参数拟合值得到的时变功率谱是平滑后的参数计算值得到的时变功率谱，但其保留了主体特征，故由二次拟合的时变功率谱合成的加速度时程与记录时程仍有较高的一致性，方法可行。

3 结 语

选用Kameda时变功率谱模型，对模型参数进行计算、拟合，最终根据时变功率谱合成爆炸地震动加速度时程。通过比较拟合爆炸地震动与实际爆炸地震动的加速度时程曲线、标准加速度反应谱、强度包线、累积穿零次数，可以发现拟合爆炸地震动与实际爆炸地震动大体上较为吻合，表明基于Kameda时变功率谱模型能够实现时频非平稳爆炸地震动的拟合。