带束层结构参数对轮胎振动噪声的影响分析
2018-07-28翟辉辉周海超张颖文
王 琦,翟辉辉,周海超,张颖文
(1.镇江高等专科学校 交通学院,江苏 镇江 212028;2.江苏大学 汽车与交通工程学院,江苏 镇江 212013)
目前,轮胎噪声已成为汽车噪声的主要组成部分,尤其是轮胎的振动噪声对汽车的乘坐舒适性影响较大。欧盟新颁布的汽车噪声法规包含新的测试方法和汽车噪声限值,目前有85%的车辆没有达到法规的要求。国内出口轮胎必须满足欧盟对噪声的法规要求。因此,降低轮胎的振动噪声具有重要的理论和工程应用价值。
轮胎结构对其各项性能影响显著,K. Yamagishi等[1]提出了乘用车轮胎最佳滚动轮廓理论,通过控制带束层和胎体的张力优化轮胎轮廓,从而提升轮胎性能。H.Yamauchi等研究表明[2],优化轮胎结构可有效抑制轮胎共振峰值的产生。B.S.Kim[3]研究了轮胎结构参数对振动噪声性能的影响,指出胎体轮廓设计对轮胎振动噪声影响显著。张典等[4]根据轮胎的双层结构耦合模型,设计了不同半钢子午线轮胎胎体结构,并对各方案轮胎的噪声进行了测试和对比分析,结果表明,不同频率下轮胎噪声的发声机理略有差别,胎体骨架材料的种类和层数影响其振动特征,进而对轮胎噪声产生影响。轮胎带束层结构决定着轮胎质量和刚度的均匀性,会产生自激振动而向外辐射噪声,虽然已有学者研究了结构对轮胎性能的影响,但仅停留在非带束层结构影响振动噪声或者带束层结构影响其他性能方面[5-8],尚未系统阐述带束层结构设计参数对轮胎振动噪声的影响规律及其原因。
本工作以295/80R22.5载重子午线轮胎为研究对象,结合模态声学传递向量技术和声学边界元理论对轮胎的振动噪声性能进行数值模拟,研究带束层宽度和角度对轮胎振动噪声的影响,并从轮胎固有频率、胎面和胎侧的振动加速度以及激励力功率谱角度分析优化后轮胎的降噪机理。
1 轮胎振动噪声的数值分析
295/80R22.5载重子午线轮胎的标准负荷为3 550 kg、标准充气压力为900 kPa。利用文献[9]中的方法建立轮胎有限元模型。分析时将轮辋和路面定义为解析刚体。橡胶部分采用CGAX3和CGAX4R单元进行模拟,钢丝帘线采用SFMGAX1和REBAR单元进行模拟。
本构模型是对理想化物质本构行为的数学和力学描述。因此,选取合适的超弹性本构模型描述橡胶材料的力学特征,对提高轮胎有限元分析的计算精度以及保证大变形分析过程中单元良好的形态、避免发生体积自锁现象具有重要作用。将测得的橡胶拉伸数据输入Abaqus软件中,并利用其自带的Ogden,Neo-Hookean和Yeoh等橡胶本构模型分别进行拟合。以胎肩垫胶为例,其材料应力-应变曲线如图1所示。
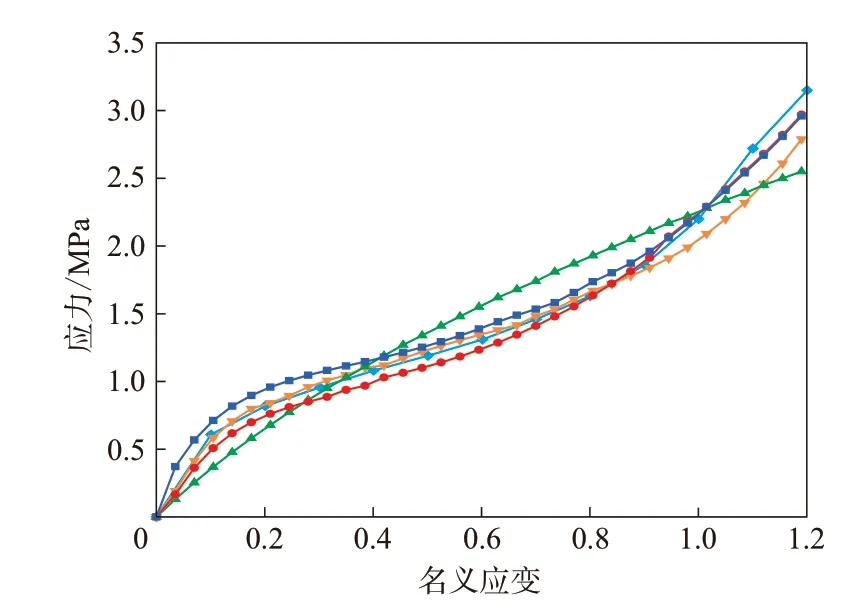
图1 不同本构模型拟合的胎肩垫胶应力-应变曲线
从图1可以看出,在名义应变小于0.5时,Yeoh本构模型拟合的应力-应变曲线与试验结果吻合较好。因此,本工作选用Yeoh模型描述轮胎橡胶的力学特性。轮胎各部位胶料的参数由单轴拉伸试验数据拟合获得。
为验证所建立的有限元模型的正确性,采用法国OROS公司生产的动态信号分析仪对轮胎的模态特征进行测试。试验时,轮胎处于悬置状态,在轮胎表面取81个测点。
试验激励的施加方式为锤击法,采用逐点锤击的方式,利用加速度传感器采集响应信号。将信号通过放大处理输入到动态信号分析仪中,每个测点测量3次,取平均值,得到0~200 Hz频率范围内的传递函数,将其导入建有轮胎模型的Modal 2分析软件中进行模态分析,从而得到轮胎前6阶径向模态的固有频率和振型[10-11]。
在Abaqus软件中,利用Block Lanczos法求出计算模态,并与试验模态的频率进行比较。结果表明,应用Abaqus软件建立的轮胎有限元模型能很好地计算轮胎的各阶模态[11]。
前期轮胎振动噪声的数值分析结果表明[11]:声学观测点的振动噪声频响函数曲线的变化趋势一致,但声压值略有差别;接地后端的声压级大于接地前端。这与葛欣等[12-13]的测试结论相吻合。
2 轮胎带束层结构对振动噪声的影响
带束层是子午线轮胎的主要受力部件,其结构参数主要包括帘布层数,帘线角度、密度和排列方式,带束层厚度、宽度和长度以及所采用的帘线结构与类型等。295/80R22.5 WSL60轮胎的带束层为“3+0”结构。其中,第1层为过渡层,第2和第3层为主要受力层,0°带束层为保护层。本工作选取第2和第3带束层的宽度和帘线角度作为设计参数,分析各参数变化对轮胎振动噪声的影响。
2.1 试验方案设计
以第2和第3带束层宽度和帘线角度为影响因子,采用正交试验方案[14]。带束层帘线角度是指帘线铺设方向所在直线与轮胎前进方向之间形成的锐角,并规定朝向左侧为正值,朝向右侧为负值。
依据载重子午线轮胎的设计原则及设计经验,选择如表1所示的因子水平。A,B,C,D分别代表第2带束层帘线角度(°)、宽度(mm)和第3带束层帘线角度(°)、宽度(mm)。根据正交试验设计原则,选择L9(34)正交试验表安排试验,对各方案轮胎的振动噪声进行计算,结果如表2所示。
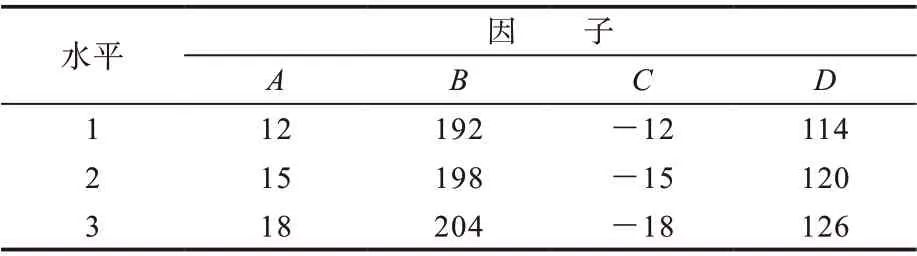
表1 带束层宽度及帘线角度设计因子与水平
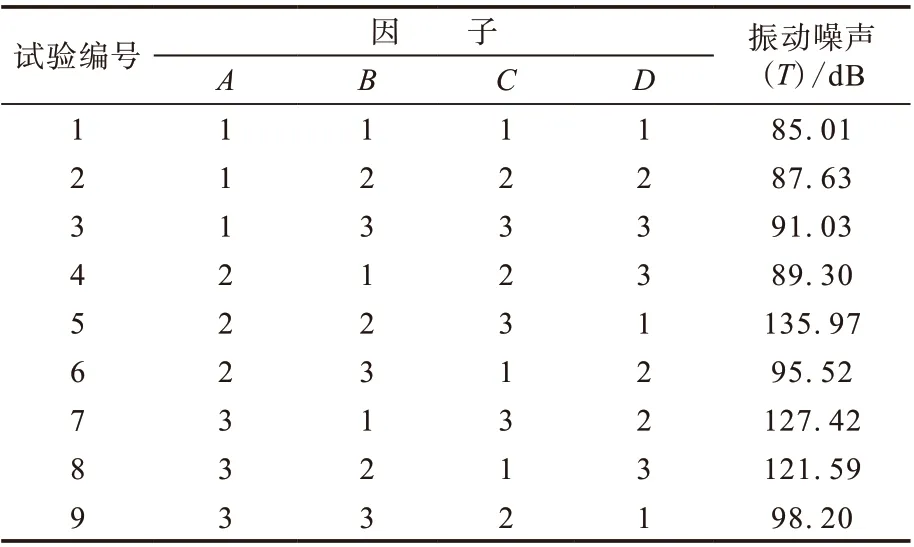
表2 带束层结构正交试验方案与轮胎噪声
2.2 优化方案
为分析带束层结构设计参数对轮胎T的影响,根据试验结果建立极差(R)分析,结果见表3。
从表3可以看出,RA>RC>RB>RD,4个因子对轮胎T的影响由大到小顺序为A,C,B,D,即对轮胎T的影响由主到次顺序为第2带束层帘线角度、第3带束层帘线角度、第2带束层宽度、第3带束层宽度。
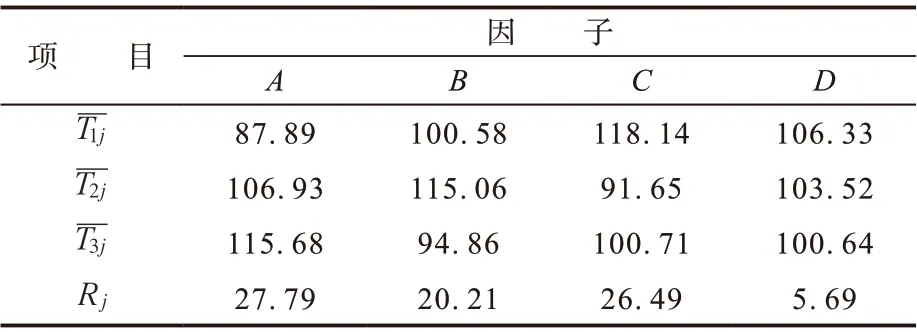
表3 极差分析结果
此外,由表3可以看出最优水平为A1B3C2D3,即当第2带束层帘线角度为12°、宽度为204 mm,第3带束层帘线角度为-15°、宽度为126 mm时,带束层结构设计方案最优,轮胎的T最小。
2.3 结果分析
经计算,带束层结构参数最优组合方案下轮胎振动噪声的A计权平均声压级为84.22 dB,较现行设计轮胎降低了7.55 dB。
带束层结构优化前后轮胎某声压观测点处的频谱曲线如图2所示。
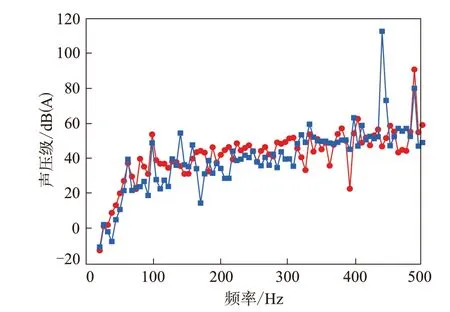
图2 带束层结构优化前后振动噪声声压频谱曲线
由图2可见:带束层结构优化轮胎的振动噪声声压峰值向高频段转移;在20~80 Hz频段内,结构优化前后轮胎的振动噪声频谱曲线变化不大;在100~320 Hz频段内,带束层结构优化轮胎的振动噪声频谱特性曲线波动相对较小,出现噪声峰值的峰数量相对较小;在320~500 Hz频段内,带束层结构优化前后轮胎的振动噪声频谱曲线变化较为明显,结构优化的轮胎在440 Hz处的振动噪声峰值显著降低。
3 降噪机理分析
分别对现行结构设计和带束层结构优化的轮胎从固有频率、胎面和胎侧振动加速度以及激励力功率谱密度角度出发,分析噪声降低的机理。
3.1 固有频率
带束层结构优化前后轮胎前6阶模态的固有频率如表4所示。
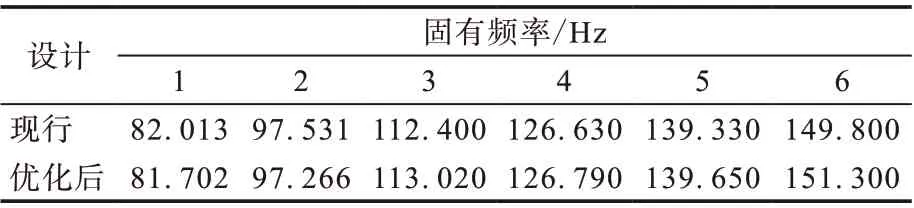
表4 带束层结构优化前后轮胎前6阶模态的固有频率
由表4可知,带束层结构优化后轮胎前2阶模态的固有频率低于现行设计轮胎,但3—6阶模态的固有频率高于现行设计轮胎。随着带束层结构优化后轮胎高阶模态固有频率的增大,轮胎的径向振动更不容易被激发,从而使轮胎振动噪声降低。同时说明,带束层结构优化设计对轮胎振动噪声性能的影响主要体现在中高频段。
3.2 胎面和胎侧振动加速度
轮胎表面振动加速度与噪声有密切联系。从频响分析的角度出发,得到滚动过程中由路面激励得到的加速度响应。轮胎滚动过程中振动主要来源于接地区和胎侧部位,因此选取接地胎面的中心点和最大断面宽处作为观测点,如图3所示。

图3 胎面和胎侧振动加速度测点
带束层结构优化前后轮胎胎面和胎侧测点的振动加速度响应如图4所示。
由图4可见:带束层结构优化后,胎面和胎侧表面测点振动加速度峰值显著降低,且出现峰值的峰数量减小;胎面测点在100~180 Hz和260~350 Hz频率范围内振动加速度的峰值显著降低,胎侧测点在110 Hz处出现了一个明显的加速度峰值,而在310~500 Hz频段内,振动加速度降低较为明显。结果表明,带束层结构对胎面测点加速度的影响主要体现在中频段,而对胎侧测点加速度的影响则主要体现在高频段。
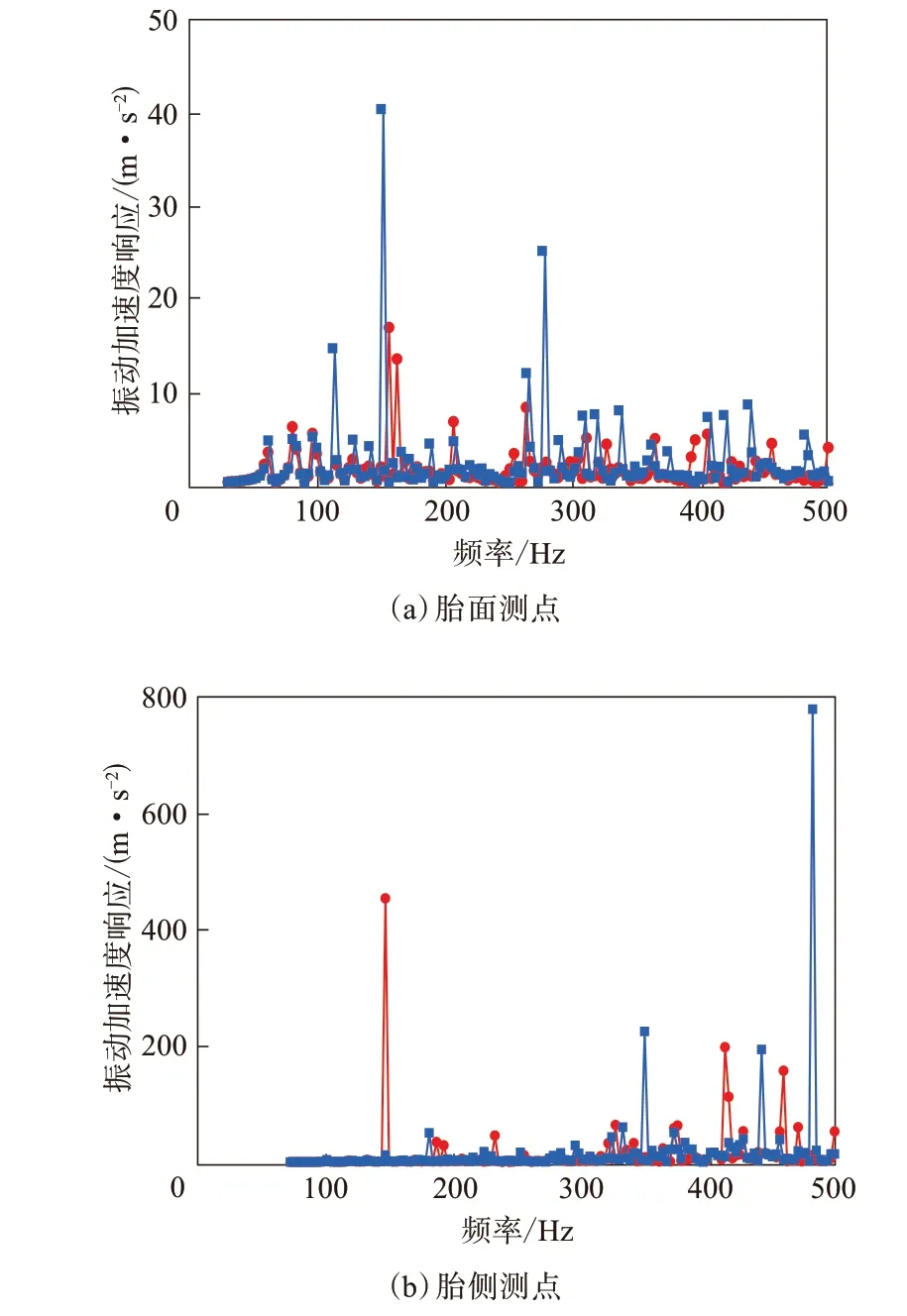
图4 带束层结构优化前后轮胎加速度频响函数曲线
3.3 激励力功率谱密度
功率谱密度是结构在随机动态负荷激励下响应的统计结果,是一条功率谱密度S(ω)-频率的关系曲线。其计算公式如下:
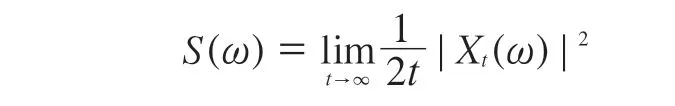
式中,t表示时间,s;Xt(ω)表示轮胎激励力加速度的复函数;ω为角频率,rad·s-1。可以看出,功率谱密度是一个非负实数,是一个频域中的量,直接反映了频域中不同频率所对应的值(误差或能量)。现行结构设计和优化设计后轮胎的激励力功率谱密度曲线如图5所示。
由图5可以看出,带束层结构优化后轮胎激励力功率谱密度的峰值和数量显著减小。联系场点声压频响函数可知,带束层结构优化后轮胎的激励力功率谱密度总体波动较小,在220~260 Hz和380~450 Hz频率范围内激励力功率谱密度显著减小,尤其在440 Hz处激励力功率谱密度降低明显。这说明振动噪声的降低是由于带束层结构优化后引起轮胎内部结构的自激激励力显著减小。
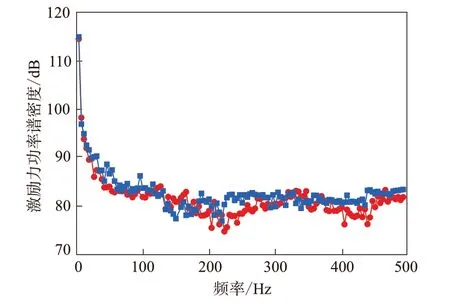
图5 带束层结构优化前后轮胎的激励力功率谱密度曲线
4 结论
采用模态声学传递向量技术和声学边界元理论对轮胎振动噪声进行模拟分析,以295/80R22.5轮胎为例,研究了不同带束层结构设计方案对轮胎振动噪声的影响,得到如下结论。
(1)比较轮胎试验模态和计算模态的特征参数,证明了振动噪声模拟分析方法的准确性和实用性。
(2)带束层结构影响轮胎振动噪声的参数由主到次顺序为第2带束层帘线角度、第3带束层帘线角度、第2带束层宽度、第3带束层宽度;优化带束层结构参数为:第2带束层帘线角度 12°,第2带束层宽度 204 mm,第3带束层帘线角度 -15°,第3带束层宽度 126 mm。
(3)带束层结构优化后轮胎高阶模态的固有频率增大,振动噪声频谱曲线波动减小,出现噪声峰值数量相对较小,且显著降低了轮胎在440 Hz处的噪声峰值,降噪量达到7.55 dB。带束层结构优化后轮胎显著降低了胎面、胎侧表面测点振动加速度和激励力功率谱密度的峰值。
本工作的研究结果为降低轮胎振动噪声提供了理论指导和现实依据。
