最大似然分类的训练样本敏感度研究
2018-07-28陆晓果王同科梁社芳
陆晓果,王同科,梁社芳,陆 苗※
(1.天津师范大学数学科学学院,天津300387;2.中国农业科学院农业资源与农业区划研究所/农业部农业遥感重点实验室,北京100081)
0 引言
遥感影像分类技术能够快速提取土地利用和地表覆盖信息,为实现资源的有效利用提供技术支撑,为研究生态环境的变化等提供重要的基础数据[1]。根据是否需要训练样本,遥感影像分类方法分为非监督分类和监督分类。非监督分类是在没有先验类别知识的情况下,根据图像自身的统计特征以及自然点群的分布情况来划分地物类别的分类技术[2]。监督分类是以建立的统计识别函数为理论基础,依据典型的样本训练方法进行分类的技术,例如最小距离法、最大似然法和神经元网络分类法等[3]。相比非监督分类,监督分类不仅能确定分类类别,而且具更高的精度。
在监督分类中,样本的选取对分类结果的精度十分重要。许多学者从样本数量和质量等方面,分析了其对分类精度的影响[4]。朱秀芳等[5]在其研究过程中发现不同分类方法的分类精度随着样本数量的不断增加而增加。Arai等[6]基于最大似然法,提出了一种纯化训练样本的方法,研究结果表明,进行纯化后训练样本的分类精度比没有纯化的训练样本得到的分类精度有了大幅提高。薄树奎等[7]基于面向对象分类方法,利用统计模型确定训练样本的最佳数量,并用遥感影像的不同波段进行验证。目前的研究通常利用多次的尝试性实验分析样本对精度的影响,缺乏算法特点和样本质量特征的综合分析。该研究以最大似然分类为基础,首先从算法原理上分析影响其分类精度的样本质量特征,然后从样本数量和样本质量两方面,分析训练样本对最大似然分类精度的影响。
1 最大似然分类的原理
最大似然法分类是基于经典统计模式识别理论的监督分类方法之一,它的实质是基于贝叶斯准则的分类错误最小的非线性分类[8]。最大似然法假设遥感影像中每个波段中的数据都呈正态分布,把多波段的遥感数据作为多维正态分布,从而来构造判别分类函数,进一步求出每一个像元相对于每个地物类别的归属概率,通过比较将该像元分到概率最大的地物类别中[9]。
假设地物类型训练样本对应的直方图服从正态分布,用正态概率分布函数(曲线)来近似该分布(图1)。第ki类地物的估计概率函数用公式(1)计算:

式(1)中,exp[ ]是e(自然对数)为底的幂函数,x是在X轴上的一个亮度值,μi是该类别训练类中所有值的估计均值,是该类所有观测值的估计方差。所以,只需存储各训练类的均值和方差,就可以计算各类中任何像元亮度值的密度函数。

图1 利用正态概率密度函数近似表示的数据分布Fig.1 Data distribution approximated by normal probability density function
如果训练数据是由多波段遥感数据组成,可以采用n维多元正态密度函数:

式(2)中,│Vi│是协方差矩阵的行列式,为协方差矩阵的逆矩阵,Mi为每类的均值,(X-Mi)T是矩阵(X-Mi)的转置。
设gi(X)为判别函数,像元X出现在ki类的概率为p(ki│X),所以

式(3)中,p(ki│X)又称后验概率,根据贝叶斯公式,则有

式(4)中,p(X│ki)为ki类中观察到像元X的条件概率;即像元X的概率实质函数;p(ki)为类别ki的先验概率;p(X)为X与类别无关条件下出现的概率,且为若干计算公式中都出现的公共项,所以在类别间比较的时候可以忽略。当待分类图像中存在若干个地物类别时需要计算并比较多个p(ki│X),然后取其中最大的p(ki│X)所代表的地物类别为待判别像元的所属类别[10]。
通过预先选择的训练样本,可以求出其平均值及方差,协方差等特征参数,从而可以求出总体的先验概率密度函数:
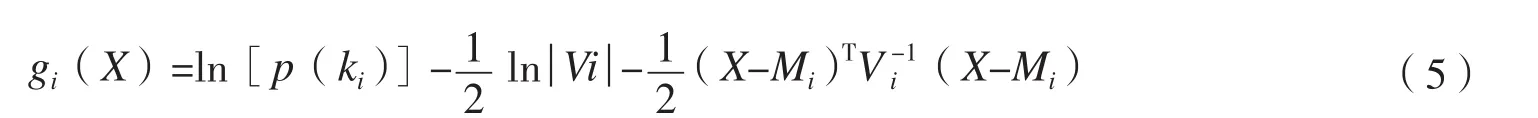
在计算并比较多个gi(X)的实际过程中,可以省略先验概率这一项,从而得到一个简单的分类规则[11]。

式(6)中,Mi是第i类的均值测度向量,Vi是第i类第k到第l波段的协方差矩阵。计算时用训练样本的协方差和均值替代Vi和Mi,便可计算出任一像元属于各类别的归属概率。若对于所有可能的j=1,2…m;j≠i有gi(X)>gj(X),将像元X归到第类中。从公式(6)中可看出,在未考虑先验概率的情况下,对于判别分类函数的主要影响因素是训练样本的协方差和均值。
2 训练样本的敏感度分析
以Landsat8影像为基础,从不同样本的数量、均值和标准差上分析训练样本对最大似然分类的影响,技术路线如图2所示。首先获取研究区域的Landsat8遥感影像,根据研究区域地表覆盖特征,确定分类类别。以已有的地表覆盖数据Globeland30为底图,采用分层随机抽样的方法选取10组不同数量的训练样本,进行相应的最大似然分类。从谷歌地球高分影像上选取训练样本,对10组分类结果进行精度评价,并分析样本数量、均值和标准差对分类结果的影响。

图2 训练样本敏感度分析流程Fig.2 Sensitivity analysis process of training samples
利用混淆矩阵进行分类的精度评估[12]。混淆矩阵是由n行n列组成的矩阵,能够说明不同类型地物的分类结果与实际地物类别的相符程度,通过混淆矩阵计算得到的总体分类精度和Kappa系数是评价分类结果的重要指标。总体分类精度(Overall Accuracy)表示对于每一个随机样本,被分类的结果和实际地物类型一致的概率[13]:

式(7)中,Pij表示矩阵中的元素,i,j=1,2…n,Kappa系数考虑了误差矩阵中所有的因子,能够全面反映总体的分类精度:

式(8)中,q是混淆矩阵的总列和,即总类别数;Pij为混淆矩阵中第i行、第i列的值,也是被正确分类的像元数;Pi+、P+i是第i行、第i列的总像元数量;P是参与分类的总像元数。Kappa值越大,代表分类的精度越高。
3 研究区域与数据
研究区域位于天津宝坻区中西部,地理位置为纬度39.34°~39.41°,经度117.13°~117.21°。该研究区域地势平坦,主要以耕地为主,靠近水域。该研究所用数据是从地理空间数据云网站(http://www.gscloud.cn/)下载的Landsat8影像(行列号为122/23),成像时间为2016年5月24日。该文选取30m空间分辨率的海岸波段、蓝波段、绿波段、红波段、近红外波段、短波红外1、短波红外2和卷云波段进行波段叠置得到研究区域的遥感影像如图3。
以2010年的30m全球地表覆盖数据产品Globeland30为底图,采用分层随机抽样的方法,分层随机抽取图幅面积比例分别为0.1%、0.5%、1%、1.5%、2%、3%、5%、7%、10%和15%的像元作为训练样本,共计10组。各地类样本的数量和样本总数量如表1所示。同时,在谷歌地球高分影像上随机选出均匀分布的475个检验样本,经目视解译后确定样本类型,包括63个水体、311个耕地和101个建设用地的样本,利用这些样本验证不同训练样本的分类精度。
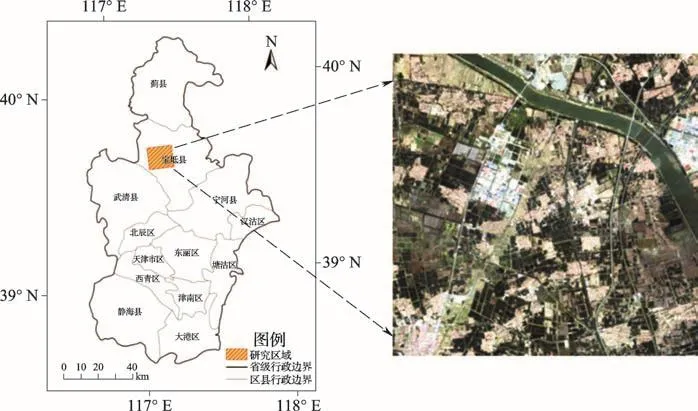
图3 研究区域位置和遥感影像Fig.3 Location and remote sensing image of the study area

表1 不同比例的10组训练样本数量Table 1 Quantity of 10 training samples in different proportion
4 结果与分析
基于表1不同组的训练样本,利用ENVI软件中的最大似然分类工具,对研究区域影像进行分类,各组分类结果如图4所示,该区域被分为耕地、建筑用地和水体3类。从图4中可看出,随着样本数量的增加,分类结果有所差别。目视上可看出,样本量从0.1%,0.5%和1%的分类结果差别较大(图4(a),(b)和(c)),后续分类结果的差别较小。

图4 不同比例训练样本的最大似然分类结果(a)0.1%,(b)0.5%,(c)1%,(d)1.5%,(e)2%,(f)3%,(g)5%,(h)7%,(i)10% 和 (j)15%Fig.4 Maximum likelihood classification results of training samples with different proportions(a)0.1%,(b)0.5%,(c)1%,(d)1.5%,(e)2%,(f)3%,(g)5%,(h)7%,(i)10%and(j)15%
4.1 不同样本数量的分类结果精度评价
利用检验样本对各分类结果的精度进行检验,kappa系数和总体精度的计算结果如图5所示。总体上看,总体分类精度和Kappa系数“先升后降”。当样本数量为0.1%时分类精度最低,总体精度是77.23%,Kappa系数是0.56。随着样本数量的增加,分类精度随之增加。当样本数量达到总体样本的1%时分类精度最高,即总体精度是82.4%,Kappa系数是0.70。之后继续增加样本的数量,分类精度反而下降;在样本数量高于总体样本5%之后出现微小波动,随后趋于平稳。当样本量较少时,不能较好的反映不同类型地物的均值和方差,参数值的估计不够准确,使得分类结果精度较低。当样本量在0.5%到1%时,通过训练样本能准确估算各地物类型的均值和方差,因此分类精度较高。当样本再逐渐增加时,样本的纯度不够,干扰因素增多,因此精度开始下降。分类精度的“先升后降”和Hughes现象一致[7]。

图5 不同比例训练样本量的总体精度Fig.5 Overall accuracy of training sample quantity with different proportion
4.2 样本均值对分类精度的影响
选择能反映水体、建筑用地和耕地特征的典型波段,分析样本均值对分类精度的影响[14]。水体选择海岸波段、蓝光波段和绿光波段,建筑用地选择绿光和两个短波红外波段,耕地选择蓝光、绿光和红光波段,不同比例训练样本的均值和检验样本均值如图6(a)-(i)所示。总体来看,当样本量是0.1%时,训练样本均值和检验样本均值差异最大,在1%样本量处,和检验样本的均值比较接近,随后两者的接近程度逐渐稳定。以水体的蓝光波段为例,0.1%的训练样本在蓝光波段的均值是9 917,和检验样本的均值10 149差别最大,1%的检验样本在该波段的均值是10 030,和检验样本最接近;随着样本量的增加,两者接近程度逐渐下降,并且趋于稳定。其他波段和地物类型都表现出相似的趋势,该趋势和图5不同比例训练样本的总体精度一致。这说明当训练样本均值和检验样本差别较大时,分类精度较低,如0.1%训练样本;训练样本均值和检验样本比较接近时,分类精度较高,如1%训练样本。
4.3 样本标准差对分类精度的影响
各训练样本正态密度函数的在不同波段存储除了与均值有关外,还和方差有关系。为了使单位一致把方差变形为标准差[15]。与样本均值分析过程相同,分别比较三类不同数量训练样本和检验样本在其典型波段的标准差,如图7(a)-(i)所示。当样本量为0.1%时,训练样本标准差的值与检验样本差距最大,并且在该样本数量下的分类结果精度最差,当样本数量为1%时,训练样本标准差的值与检验样本差距最小,在该样本数量下的分类结果精度最高。以水体的蓝光波段为例,在样本数量为0.1%时,检验样本的标准差比训练样本的标准差大180,此时分类精度最低,当样本数量为1%时,检验样本的标准差仅比训练样本的标准大10,此时分类精度最高。分析表明不同数量的训练样本的标准差对分类精度的影响与均值对分类精度的影响一致,当训练样本的标准差越接近检验样本的标准差时,分类结果越精确。

图6 不同数量的水体、建筑用地和耕地训练样本均值和检验样本的比较Fig.6 Comparison of mean values between training samples and test samples of water,building and cropland
5 结论
该文采用了最大似然分类算法对研究区域的遥感影像进行土地分类。首先利用现有的地表覆盖数据选取10组不同数量的训练样本进行分类,然后基于真实的检验样本分析不同数量和质量的训练样本对分类结果的影响,得到的结论如下。
(1)在样本数量方面,随着样本量的增加,分类精度呈现先升后降,然后趋于稳定。在最大似然分类过程中,训练样本数量的选取存在临界值,当到达临界值时即可满足分类结果的精度要求,随后即使增加样本的数量也无法显著提高分类结果的精度。较多的样本量会给分类结果带来误差和干扰,因此增加样本的数量不一定能持续提高分类的精度。
(2)在样本质量方面,以样本的均值和标准差为特征,分析样本质量对分类结果的影响。分析发现,训练样本的均值和标准差与检验样本的接近程度影响分类精度,当训练样本均值和标准差与检验样本比较接近时,分类精度较高,反之分类精度较低。
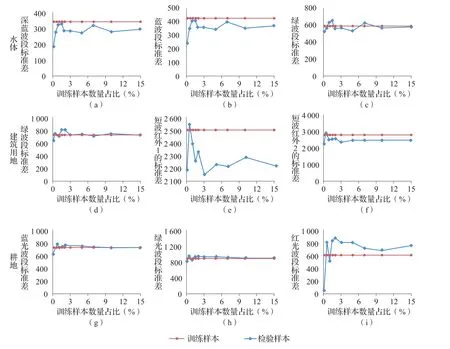
图7 不同数量的水体、建筑用地和耕地训练样本的标准差和检验样本比较Fig.7 Comparison of standard deviation between training samples and test samples of water,building and cropland
该文主要分析了样本数量和质量对最大似然分类的影响,但是在土地利用分类的实际利用中,不同地物之间的可分离性也会影响训练样本数量的选择。今后会加入地物分离度等其他对分类结果有影响的不确定性因素,并综合考虑其它监督分类方法如支持向量机、机器学习等算法,进一步探讨不同训练样本对不同分类方法精度的影响。
