应用三维结构光和小波分析进行钢轨波磨检测

李 坪，王培俊，陈 鹏，徐 浩

(西南交通大学机械工程学院，成都 610031)

钢轨波浪形磨损简称波磨，是钢轨在投入使用后随着运营时间的增加，逐渐在钢轨顶部沿其纵向出现一种规律性的类似波浪形状的周期性不平顺磨损现象[1]。在钢轨波磨区段，因为钢轨轨面的不平顺导致钢轨承受更大的动荷载，造成铁路钢轨的扣件发生松动从而引起钢轨下沉，严重影响列车行车安全。国内外学者对波磨的产生原因进行了详细研究[2-5]，总结出了很多影响钢轨波磨的因素，但由于其复杂性导致目前对于直接引起钢轨波磨的原因尚没有统一观点。对波磨的检测进展较缓慢，国内大多采用专用卡尺进行人工抽样检测，效率低下[6]。进口的波磨检测仪如英国的Bi-CAT等价格昂贵，难于推广使用。

近年来国内外学者提出了各种新的波磨检测方法[6-9]，主要包括弦测法、惯性基准法和机器视觉法。弦测法和惯性基准法获取数据的准确度和丰富度都没有机器视觉高，而目前机器视觉检测多数是基于平面二维检测，精度相对于三维结构光较低。三维结构光具有非接触、快速获取大量信息、检测结果可靠和易于实现自动化等优点[10]，本研究提出了将三维结构光技术应用到钢轨波磨检测的新方法。通过结构光扫描仪获取完整的钢轨三维点云，通过数据处理可以准确地找到钢轨纵向不同截面的波磨信息，比弦测法和惯性基准法更加灵活，数据更加充足。

波长的成分一般是随机的或有限个波长的混合[11]，所以波磨的检测具有难度。有学者尝试用分形理论来解释波磨[11-12]，但只能说明波磨的损伤程度，不能给出具体的检测数据。小波分析是傅里叶分析之后又一重要分析数学方法，能够有效地从各种信号中提取有用的信息，通过伸缩和平移等运算对函数和信号进行多尺度分析，从而解决许多傅里叶变换不能解决的问题。本研究提出利用小波分析方法分析波磨中各种频率成分的波磨，分别得到每一种波长的幅值作为钢轨波磨的检测数据。实验表明，本方法能有效地分析出波磨的各个频率成分。综合应用三维结构光与小波分析技术，是一种有效、直观的波磨检测方法。

1 三维结构光检测

1.1 三维结构光检测系统结构

三维结构光检测系统结构如图1所示。该检测系统是基于光学三角法测量原理，由左右两个摄像头加投影仪组成一个双目视觉检测系统。其中投影仪负责向钢轨投影周期变化光栅，左右相机负责拍摄带有光栅的照片，通过解码光栅恢复钢轨表面三维结构信息。

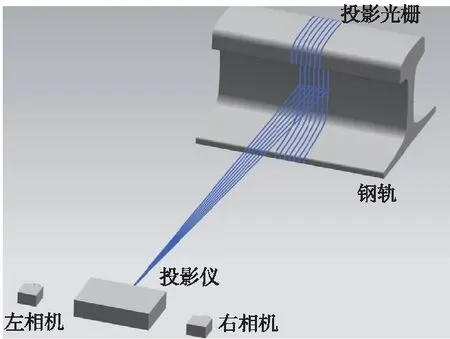
图1 三维结构光检测系统结构

1.2 三维结构光检测成像原理

如图1所示。将一个周期内均匀移动的光栅投影到钢轨表面，由于钢轨表面形状会引起光栅变形，所以设从相机获取的变形光栅如下[11]

I(x，y)=R(x，y){C[0.5+0.5cosφ(x，y)]}

(1)

式中，R(x，y)为钢轨表面不均匀的反射率，包括灰度和色度信息；C为均匀的投影光强；φ为光栅条纹的相位。

由于这3个参数均为未知量，所以至少需要3张以上的变形光栅图才能解出这3个参数。由相移条纹成像法可知，将一个周期内的投影光栅均匀移动N(≥3)次，则每次移动2π/N相位，由这N幅图像即可求出未知量。由于钢轨外形为三维表面，因此设其表面高度分布为h(x，y)，则相位可以表示为

φ(x，y)=2πx/p0+2πh(x，y)/λe

(2)

式中，p0为条纹周期，λe为等效波长，一个等效波长会引起2π相位变化量的高度变化。式(2)中第一项为投射表面为平面时的表达式，第二项为三维表面高度差引起的增量。根据式(1)中求出的φ(x，y)即可解出高度分布h(x，y)，结合系统标定参数即可解出每一个点在三维空间中的位置。

2 小波分析理论

2.1 小波函数

设φ(t)∈L2(R)，当其傅里叶变换满足容许性条件[13]

(3)

称φ(t)为基本小波或母小波。

对φ(t)进行尺度伸缩和空间平移后得

(4)

式中，a为伸缩因子；b为平移因子；式(4)称为连续小波。

2.2 小波变换

设函数f(t)∈L2(R)，则对该函数和小波函数进行内积计算称为小波变换，也称小波系数

(5)

小波变换后的重构公式为

(6)

式(6)中伸缩因子a、时间t和与时间有关的平移因子b都是连续的。而波磨数据是通过采样N个点进行分析，因此需要将上述连续函数变换为离散函数。对参数a和b按公式(7)处理

(7)

代入公式(4)得到离散小波

(8)

根据公式(5)和公式(8)得到函数f(t)的变换系数

(9)

根据公式(6)和公式(8)得到函数f(t)的重构公式

(10)

公式(8)中取a0=2，b0=1，得到如下二进小波

(11)

2.3 多分辨率分析和Mallat算法

S.Mallat提出的多分辨率分析概念是从构造正交小波基演化而来，从空间的概念上说明小波的多分辨频率特性。其实质是对信号频率进行1/2分解，得到低频部分A1和高频部分D1。若分解层数大于1，则对低频部分A1进行再次分解，高频部分D1不予考虑，逐层分解。

Mallat算法又称塔式算法[13]，它是通过小波滤波器H、G和h、g对信号进行分解和重构，以获得所需要的信号特征。分解算法为

(12)

分解算法图解如图2(a)所示。

重构算法为

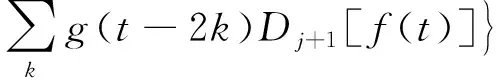
(13)

重构算法图解如图2(b)所示。

图2 Mallat算法图解

3 小波分析在波浪形磨损中的应用

波浪形磨损根据波长可以分为波纹磨耗与波浪磨耗两种[14]。其中波纹磨耗波长为30～80 mm，波浪磨耗波长大于80 mm。从实际的研究调查中可以发现[15]，客货混运铁路由于列车轴重大，钢轨波磨的波长较长，一般为200～300 mm，且深度较深。地铁线路运营列车轴重较轻，运行速度较低，小半径曲线较多，车站间距较短，列车频繁制动、起动，钢轨波磨的波长一般为30～80 mm，且深度较浅。高速铁路中钢轨波磨的波长较短，在线路高速区一般为120～150 mm，线路低速区约为60～80 mm，波磨深度较浅，一般在0.04～0.10 mm范围内。

3.1 采样信号

本研究通过分辨率为400×300的双目结构光扫描仪扫描得到钢轨点云Φ。通过编程提取钢轨纵向不同位置截面的点云Φi(i=1，2，3…)，结构示意如图3所示。

对Φi数据进行采样，根据香农采样定律，采样频率fs和最大频率fmax之间应满足关系：fs≥2fmax。则采样波长Ls与最小波长Lmin之间的关系为：Ls≤Lmin/2。考虑最小限制波长为30 mm，所以取Ls=10 mm。最终得到截面Φi(i=1，2，3，…)的波磨数据φi(i=1，2，3，…)。

图3 钢轨波磨数据采样示意

3.2 小波函数的确定

目前探寻小波基主要采用两种方法，一是直接分析小波基的数学特性；二是分析某几种特定的小波基，定性进行比较[16]。小波基的重要特征为紧支性、正则性、对称性和消失矩。紧支性保证有优良的空间局部性质，时域上的紧支性可以避免泄露，而频域上的紧支性可以避免交叉项的影响；消失矩反映能量的集中程度，足够高的消失矩有利于检测出信号的奇异点；对称性确保子波的滤波特性有线性相移，不会造成信号的失真。满足此条件的小波基有：Daubechies小波、Coiflets小波和Symlets小波。

小波选取还要考虑小波滤波器的理想程度。以dbN小波为例，选取不同N值的幅频特性也不相同，N越大则滤波器的理想程度就越好。综合以上因素，最终确定选取db40小波。

3.3 分解层数的确定

设采样长度为D，采样间隔为T，信号的频带宽度为[0，fmax]。根据香农采样定理[17]，采样信号最高频率fmax=π/T，为了能够从[0，fmax]的频率域内滤出频率f1、f2成分，分解层数N需要满足f1/fmax=1/2N，f2/fmax=1/2N，则有

(14)

设Ti(i=1，2)为fi对应的分界波距，代入上式得

(15)

由前两节可知，分界波距为：T1=30 mm，T2=80 mm。采样间隔为：T=10 mm。代入式(15)中得N=3。

4 现场检测实验

4.1 实验条件

现场检测实验的钢轨数据采集地点为成都铁路局北车辆段编组站进站线路(到发线、调车线、牵出线、货物线及站内指定用途的其他线)，采集的点云数据为钢轨内侧工作面，且为经过磨损后的站线，长度5 m。扫描仪型号XTOM-ET-IV工业型双目扫描仪，相机像素200万，单次测量幅面400 mm×300 mm，单幅精度0.03 mm，获得点云数据中点与点的距离0.25 mm。实验设备搭载在自行研制开发的检测小车上，如图4(a)所示，采集的点云数据如图4(c)所示。检测效率的比较对象为D&F160612型数显钢轨波磨仪，如图4(b)所示，该波磨仪的检测原理是基于静态弦测法，其检测长度1 m，分辨率0.01 mm。

图4 现场实验和点云数据

4.2 实验结果

4.2.1 效率对比结果

在室外温度为30 ℃左右条件下，以检测1 m长度的钢轨作为评判标准，采样间隔为10 mm。该波磨仪的检测过程：找钢轨顶面→移动游标卡尺读数并手动记录数据。每次检测都以第一个点作为基准点。

本研究的检测过程：结构光扫描仪放在检测小车上拍摄，拍摄流程为：标定→喷显影剂→贴标识点→扫描，1 m钢轨需要拍摄3幅拼接而成。耗时对比如表1所示。

从表1可以看出，结构光扫描仪的检测效率高于传统波磨仪。结构光检测主要耗时在标定模块，但测量时只需要标定一次即可，所以若是测量连续的数据，结构光的效率远远高于波磨仪。波磨仪主要耗时在测量读数模块，由于采样间隔为10 mm，所以1 m的钢轨实际的采样点数为100个，但是受波磨仪的长度限制，其采样点数实际为80个左右，且不一定与钢轨纵向平行，也即数据的准确度有所降低。由于是接触式检测，实验发现波磨仪的损耗过大，采样3 m后游标卡尺大约磨耗0.05 mm，而结构光检测则没有这个问题。

表1 检测时间记录

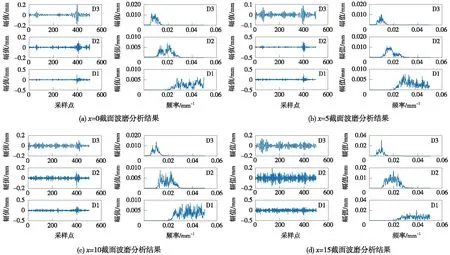
图6 4个截面波磨分析结果

4.2.2 数据测量结果

从以上的理论分析可知，在db40分解3层的情况下，每一层的理论频率和波长如表2所示。其中A为近似信号，D为细节信号。

表2 理论频率和波长

将图4(c)中的数据与标准模型重复配准3次后得到3个配准结果，然后按照图3所示取钢轨纵向4个截面Φi(i=1，2，3，4)，其中，Φ1为x=0 mm截面，Φ2为x=5 mm截面，Φ3为x=10 mm截面，Φ4为x=15 mm截面(以钢轨工作面方向为x正方向)。将3组数据中每一个采样点坐标取平均后的数据如图5(a)所示。利用波磨仪采集得到的86个数据如图5(b)所示。

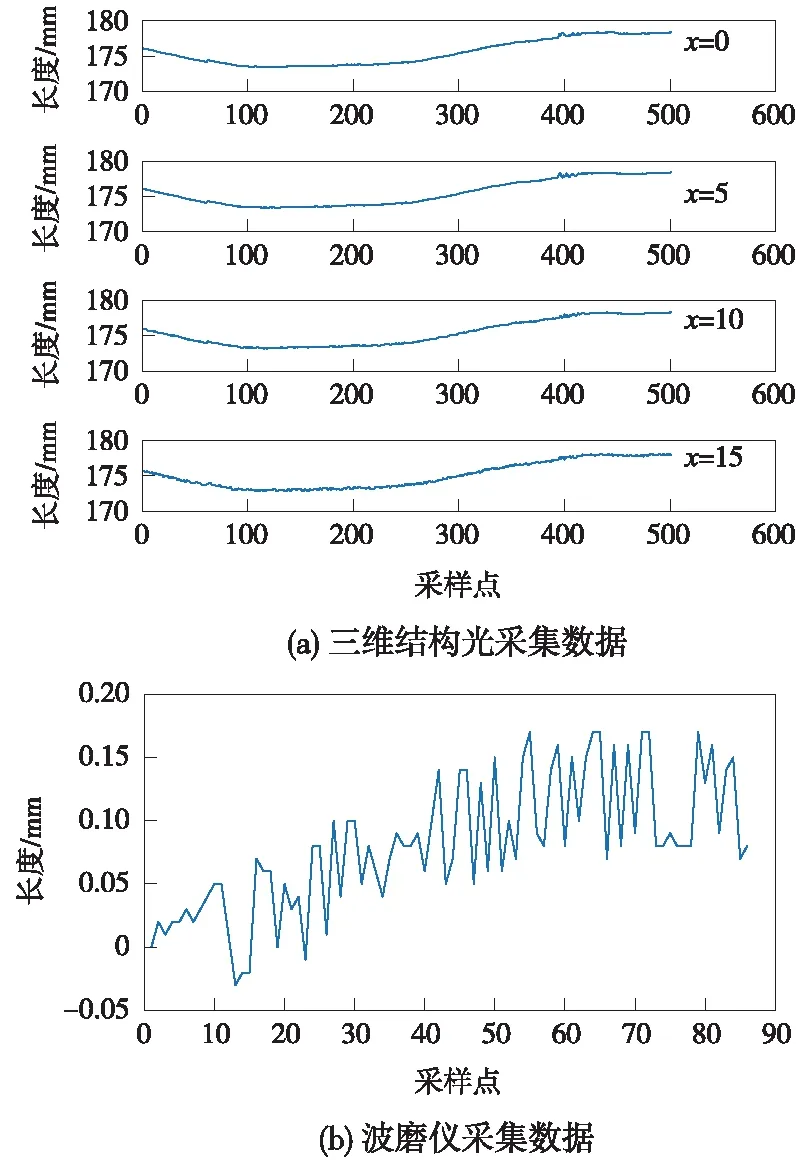
图5 不同仪器采集波磨数据

对这4组数据利用db40小波进行3次分解后，分析结果如图6所示。

对波磨仪采集的数据利用db40小波进行3次分解后，分析结果如图7所示。

图7 波磨仪数据小波分解结果

从图6中可以看出，在x=0截面波长主要集中在D3中，其幅值在0.01～0.015 mm；在x=5和x=10截面波长主要集中在D2和D3中，其幅值在0.01 mm左右；在x=15截面波长在D1，D2，D3中均有分布，且在D3中幅值达到了0.03 mm。而4个截面中x值越大越靠近工作面，说明钢轨在越靠近工作面处其波浪形磨损也就越明显，与实际情况吻合。

对比图6和图7可以看出，x=10截面更加接近波磨仪所采集的数据。也就是说x=10截面所得数据更加接近实际磨耗，从图4(b)中也可以看出波磨仪的检测位置为侧面x=10 mm处。综合图6、图7和铁道部的钢轨磨损标准[14]可知，该段铁路尚未达到磨损更换要求，可以继续使用。

4.2.3 结构光测量精度

实验过程：取尚未磨损的钢轨作为评判标准，利用结构光拍摄3幅(相当于波磨仪一次的测量行程)连续点云，然后与标准CAD模型匹配，依次取上一节中的4个截面，以采样间距10 mm采取n个点，取这n个点与标准模型的间距dij(i=1，2，3，4，j=1，2，3…n)，再计算每一个截面上n个点的平均距离Di(i=1，2，3，4)，重复以上实验过程3次，然后取平均值。测得数据如表3所示。

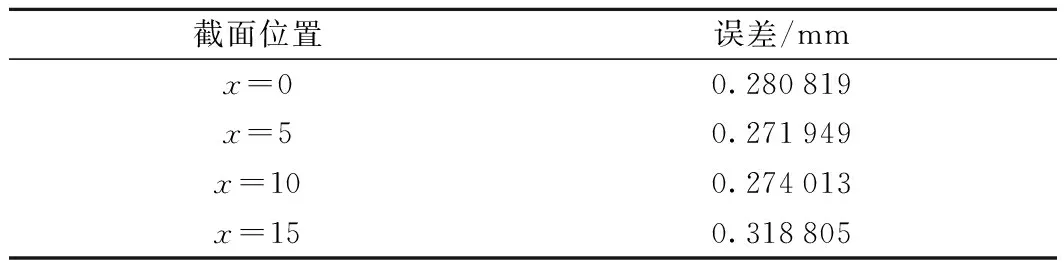
表3 结构光测量误差

从表3可以看出，结构光测量的误差为0.28～0.31 mm，小于标准限值[18]，满足精度要求。

本研究方法可对检测数据进行自动分析处理，检测结果直观、数据量丰富。而传统的波磨仪只能手工记录检测数据，工作量大，出错的可能性也大。

5 结论

(1)结构光检测能够获取钢轨波磨多个截面的数据，相较于传统的波磨尺数据量更大，获取的分析结果更多，是波磨以及铁路其他参数检测的有效方法。

(2)结构光扫描检测波磨相对于传统波磨仪具有测量效率高、测量寿命更长等优点。实验表明，在测量较长的数据量时，结构光的优势更加明显，且不存在接触磨损。

(3)小波分析能够不受时域的影响，对于时域上频率不停变化的信号依旧能够分析出频率成分。对于钢轨波磨，能够有效地分析出波磨中不同波长的成分，是一种有效的检测钢轨波磨的方法。

(4)将结构光检测和小波分析方法结合起来作为新的波磨检测方法，具有检测方便、效率更高、结果准确等优势。