填充式防护结构弹道极限方程的差异演化优化
2018-07-28贾光辉姚光乐张帅
贾光辉, 姚光乐, 张帅
(1. 北京航空航天大学 宇航学院, 北京 100083; 2. 中国空间技术研究院 总体部, 北京 100094)
随着中国载人航天工程的发展,填充式防护结构成为航天器防护的重点[1]。在航天器的防护问题中,弹道极限方程一直是最主要的研究内容之一,也是航天器空间碎片撞击风险评估失效判断的依据[2]。为此,需要对填充式防护结构弹道极限方程的准确建模进行研究。
文献[3]为获得适用于中国航天工程特定填充式防护结构的弹道极限方程,采用穷举法对不同预测指标[4]组合下NASA 填充式防护结构弹道极限方程[5]进行双待定参数修正,修正后方程的预测能力更优。由于穷举法具有全空间搜索能力,其结果为所枚举变量的最优值,因此,文献[3]所获得的弹道极限方程的预测能力基本上为最优。但此方法的计算量与待定参数个数呈指数型的关系,因此不适合待定参数较多且数据量大的弹道极限方程建模。
差异演化(Differential Evolution,DE)算法[6]是一种基于群体差异的算法,具有全局搜索能力,且简单易用,收敛速度快[7]。文献[8]通过函数测试表明,差异演化算法在绝大多数情况下比遗传算法等具有更强的全局搜索能力。
除了借鉴NASA 填充式防护结构弹道极限方程之外,建立国内填充式防护结构的弹道极限方程具有重要意义。文献[9]通过量纲理论建立了该弹道极限方程形式,确定该方程中包含的3个待定系数和8个待定指数之后,即完成该方程的建模工作。为了求得这些待定参数的数值,本文将此方程中的指数和系数作为优化变量,预测指标(概率型指标和误差型指标)[4]作为目标函数,基于国内数据,采用差异演化算法对方程中的优化变量进行确定。
1 差异演化算法基本原理
差异演化算法的演化过程与遗传算法类似,也包括种群初始化、变异、交叉和选择操作。差异演化是基于实数编码的演化算法,因此可将个体视为实数设计变量组成的向量。差异演化算法首先创建种群,然后对种群的所有个体进行变异操作,接着进行离散交叉生成中间个体,最后中间个体与父个体进行竞争,较优的个体被选中,形成数目不变的下一代新种群。
1.1 种群初始化
在D维空间随机产生个体数为NP的种群,其各个个体的变量为
i=1,2,…,NP,j=1,2,…,D
(1)
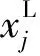
1.2 变 异
变异是差异演化算法的关键步骤,基于个体向量差进行。设当前种群中的个体为Xi(t),t为演化代数。从当前种群中随机选择3个个体Xr1(t)、Xr2(t)和Xr3(t)(r1≠r2≠r3≠i),取后2个个体向量的差(Xr2(t)-Xr3(t)),使用缩放因子F调节大小,然后与第1个个体向量Xr1(t)求和,获得变异后的个体hi(t+1):
hi(t+1)=Xr1(t)+F(Xr2(t)-Xr3(t))
(2)
式中:F为缩放因子,取值范围一般为[0,2]。
1.3 交 叉
交叉操作可以增加种群的多样性,变异后的个体hi(t+1)和种群中当前的演化个体Xi(t)通过离散交叉,生成中间个体vi(t+1):
vij(t+1)=
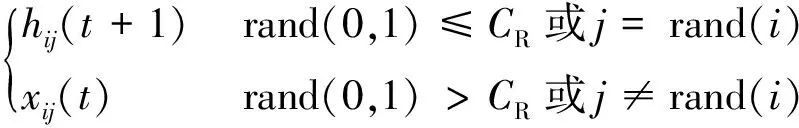
(3)
式中:rand(i)为[1,D]之间的随机整数;CR为交叉概率,取值范围一般为[0,1]。
1.4 选 择
中间个体vi(t+1)与当前演化个体Xi(t)的适应度进行比较:
Xi(t+1)=
(4)
式中:f表示适应度函数。
通过上述变异、交叉和选择,对种群中的每个个体进行循环操作,得到下一代种群,如此演化若干代,获得优化问题的最优解。
2 测试函数演化结果
对基本差异演化算法进行编程实现,以文献[10]中的3个测试函数进行程序验证。
Ackley函数(f1):
xi∈[-32,32]
(5)
Rastrigin函数(f2):
xi∈[-5.12,5.12]
(6)
Griwangk函数(f3):
xi∈[-512,512]
(7)
式(5)~式(7)中,n=20,即各函数的优化变量个数,其中Ackley为单峰函数,Rastrigin、Griwangk为多峰函数。优化计算时,NP的取值原则参考文献[2]:5D≤NP≤10D,种群大小NP取100,缩放因子F取0.5,交叉概率CR取0.3。
对3个函数进行差异演化计算时,在每一代的种群中选择出适应度最小的个体,作为最优个体。理论上讲,需要分别画出最优个体的各个变量变化曲线,并进行讨论。鉴于各个函数都有20个变量,若逐一对变量画图分析,就会过于冗杂,因此只对每个函数的20个变量绝对值求和,并进行画图分析。
在对函数f1、f2和f3优化时,最优个体的变量绝对值之和与适应度随演化代数的变化曲线如图1(a)~(c)所示。
由图1可知,3个函数在种群不断演化过程中,最优个体逐渐到达最优。函数f1和f3在演化代数大于300以后,变量绝对值之和与适应度都基本为零,趋于平稳。函数f2在代数大于1 800以后,变量绝对值之和与适应度都基本为零,趋于平稳。3个函数的优化结果如表1所示。
由表1可以发现,函数f1、f2和f3的优化结果与理论结果误差小于0.000 2,因此本文的差异演化算法程序可得到正确的结果。

图1 各函数最优个体的变量绝对值之和与适应度随演化代数变化曲线Fig.1 Changing curves of sum optimal individual absolute variables and fitness with generation for each function

测试函数理论最优值演化代数优化结果f105000.00006f2020000.00001f305000.00012
3 综合建模方程
3.1 一般形式
针对国内填充式防护结构形式,文献[9]利用量纲理论建立了一种合适的填充式防护结构弹道极限方程形式,称之为综合建模方程,其形式如下所示。
1) 低速区:V≤VL。
(8)
2) 高速区:V≥VH。
(9)
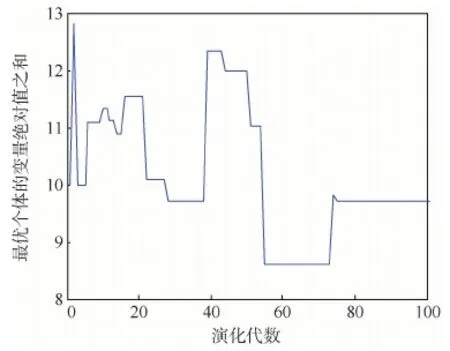
3) 中速区:VL dc=dc,V=VL(VH-V)/(VH-VL)+ dc,V=VH(V-VL)/(VH-VL) (10) VL=2.6(cosθ)-0.5 VH=6.5(cosθ)-0.75 上述弹道极限方程共涉及16个物理变量,dc为临界弹丸直径,cm;V为弹丸速度,km/s;VL为低速区与中速区的分界速度,km/s;VH为高速区与中速区的分界速度,km/s;ρp为弹丸密度,g/cm3;tb为前板厚度,cm;σb为前板强度,ksi(1 ksi=0.145 MPa=0.145 N/mm2);S为板间距,cm;tw为后板厚度,cm;ρw为后板密度,g/cm3;σw为后板强度,ksi;σce为玄武岩填充层的强度,ksi;σca为Kevlar填充层的强度,ksi;mce为玄武岩填充层的面密度,g/cm2;mca为Kevlar填充层的面密度,g/cm2;θ为撞击角度,rad。此方程的待定参数共11个,包含3个待定系数和8个待定指数,待定系数为ηi(i=1,5,8),待定指数为ηj(j=2,3,4,6,7,9,10,11),均无量纲。 本文在进行综合建模方程的待定参数优化时,优化的目标函数对应多个预测指标(总体预测率、安全预测率、平均相对误差平方和)。平均相对误差平方和为误差型指标,其大小由预测错误的实验直径与方程预测直径之间的偏差确定;总体预测率和安全预测率为概率型指标,其大小是由各类样本数和方程预测正确的个数确定。可见,表示概率型指标的2个函数为整数运算结果,不连续。同时,这3个目标函数值的确定依赖于综合建模方程和实验数据,不能获得显式表达式,因此为隐函数。所以,综合建模方程的待定参数优化问题本质是隐式、不连续函数的多目标优化问题,面向解析函数的优化方法都不适用于本问题。 分层序列法是多目标决策的一种方法,其本质是按一个原始目标选择若干可行解,再按另一目标缩小可行解的范围,直至所有目标分析完成为止[11]。本文使用分层序列法时,令目标的先后顺序依次为F1(总体预测率)、F2(安全预测率)、F3(平均相对误差平方和),即首先选择总体预测率最大的可行解,然后在这些可行解中筛选出安全预测率最大的可行解,最后在筛选出的可行解中,将平均相对误差平方和最小的解作为最优解。 在综合建模方程形式中,所有待定系数及待定指数统称为待定参数,将其作为优化变量,形成优化数学模型。 优化变量为 x=(x1,x2,…,x11)=(η1,η2,…,η11) 目标函数为 (11) 约束条件为 (12) 对综合建模方程的待定参数进行优化时,优化变量一共有11个。若采用穷举法优化,如文献[3](优化效果非常好)的变量范围与步长取值做法,则枚举个数为[(1.5-0.5)/0.01+1]11=1.1×1022。可见穷举法的枚举个数过大,导致运算时间过长且运算所占内存过大,因而不能完成优化计算。采用差异演化算法时,种群规模NP取60,演化代数的最大值N取100,则总枚举个数为(N+1)NP=6 060。与穷举法相比,优化效率获得极大提升。 基于文献[3]所使用的所有国内数据,即来自于文献[12]的31个数据和文献[13]的3个数据,采用差异演化算法进行优化。 在差异演化过程中,将适应度的比较改进为3个目标函数的比较,比较方式为多目标分层序列法。经过种群100代的演化,各个优化变量由初始值改变到优化值,如表2所示。在演化过程中,最优个体的变量绝对值之和随演化代数变化曲线如图2所示,最优个体的总体预测率与安全预测率随演化代数的变化曲线如图3所示,最优个体的平均相对误差平方和随演化代数的变化曲线如图4所示。 表2 优化前后变量的数值比较 图2 最优个体的变量绝对值之和随演化代数变化曲线Fig.2 Changing curve of sum of optimal individual absolute variables with algebra 图3 最优个体的预测率随演化代数变化曲线Fig.3 Changing curves of predicted rate of optimal individual with algebra 由图2可知,在演化代数大于80以后,最优个体的变量绝对值之和不再发生变化。由图3可知,在演化代数大于30以后,最优个体的2个概率型指标不再发生改变,总体预测率达到82.35%,安全预测率达到100%。由图4可知,在演化代数大于80以后,最优个体的平均相对误差平方和的变化量在0.001以内,其最终值为0.001 3。可见,采用差异演化算法求解11个待定参数的弹道极限方程建模问题,可以获得满意的结果。同时可以看出,差异演化代数到达80时,基本上已经实现了综合建模方程所有待定参数的优化确定,表明了此种算法的高效性。 优化后的方程是否具有适用性,需要运用其他来源的实验数据进行检测。本文选用文献[14]的12个实验数据(4个数据为全玄武岩填充层结构,8个数据为玄武岩/Kevlar填充层结构)和文献[15]的37个实验数据(全为玄武岩/Kevlar填充层结构)。方程预测结果为:总体预测率为83.67%,相对于82.35%提升了1.32%,安全预测率为95.92%,相对于100%降低了4.08%,平均相对误差平方和为0.008 6,相对于0.001 3增加了0.007 3。可见,采用差异演化算法获得的方程具有一定普适性。 进一步细分对这49个实验数据的分类预测能力,图5绘出了参数确定后的综合建模方程对此实验数据的预测效果。可见,后板失效的数据一共有33个,其中有2个数据预测错误,则后板失效数据的预测正确率为93.94%;后板未失效的数据一共有16个,其中有6个数据预测错误,则未失效数据的预测正确率为62.5%。虽然弹道极限方程对未失效数据的预测率较低,但由图5可见,预测错误的未失效数据距离直线1非常近,表明优化后的方程误差非常小。 图4 最优个体的平均相对误差平方和随演化代数变化曲线Fig.4 Changing curve of average sum of squared relative errors of optimal individual with algebra 图5 优化后方程对实验数据的预测效果Fig.5 Experimental data prediction results using optimized equation 1) 本文对差异演化算法进行了编程实现,通过对3个包含20个变量的典型数学函数的优化验证,优化结果与理论结果在0.000 2以内,表明本文所编差异演化优化程序结果可信。 2) 采用差异演化算法,基于文献[3]中使用的国内实验数据,对综合建模方程的11个待定参数进行3个目标函数的优化确定,获得了综合建模方程各个待定参数的优化值。 3) 待定参数确定后的综合建模方程,对优化过程中所采用的实验数据预测情况为:总体预测率为82.35%,安全预测率为100%,平均相对误差平方和为0.001 3;对其他来源的49个实验数据预测情况为:总体预测率为83.67%,安全预测率为95.92%,平均相对误差平方和为0.008 6。经比较发现,概率型指标的偏差在5%以内,误差型指标的偏差在0.01以内,因此,所得综合建模方程的适用性得到验证。3.2 待定参数优化模型
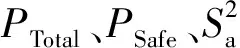
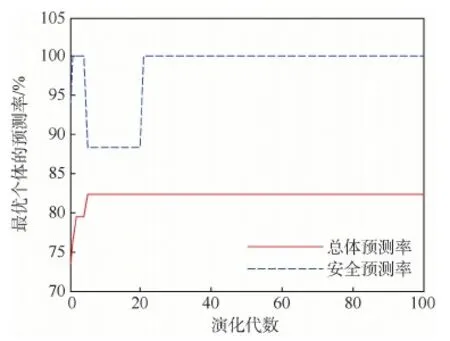
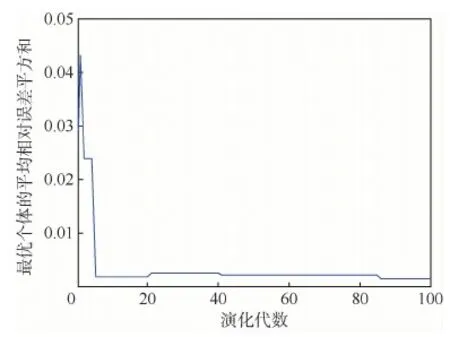
3.3 待定参数优化确定


4 结 论
