一种基于Graham扫描算法的空间点云结构化算法研究

王凯 支煜 陈浩 张毅坤

摘 要： 在过度包装检测过程中，针对商品三维重建后的散乱点云无法进行后续空隙率判定的问题，提出一种基于Denaunay三角化和凸包算法的散乱点云结构化方法。首先，因为空间点云结构复杂，所以将空间点云进行切片和投影操作，也就是降维操作；其次，对投影数据点进行结构化处理，寻找初始点，依次对投影点按照极角大小进行排序；最后利用所构造的扫描线对数据点进行筛选和结构化。实验表明，基于Denaunay三角化和凸包算法的散乱点云结构化方法处理时间短，稳定性和精度高、适用性强，完全满足过度包装检测系统。与目前方法相比，该方法有更好的适用性，能够满足大多数平台的需求。

关键词： 过度包装； 散乱点云； Graham扫描算法； Denaunay三角化； 凸包算法； 点云结构化

中图分类号： TN919.2?34 文献标识码： A 文章编号： 1004?373X（2018）14?0139?04

Research on space point cloud structuring algorithm

based on Graham scanning algorithm

WANG Kai1，2， ZHI Yu2， CHEN Hao2， ZHANG Yikun2

（1. Xian Institute of Measurement and Testing Technology， Xian 710068， China； 2. Xian University of Technology， Xian 710048， China）

Abstract： In allusion to the problem that the subsequent voidage judgment cannot be performed due to the scattered point cloud after 3D reconstruction of commodities during the excessive packaging detection process， a scattered point cloud structuring method based on Denaunay triangularization and convex hull algorithm is proposed. As the structure of the space point cloud is complex， the slicing and projection operations （also called dimensionality reduction operations） are conducted. The projected data points are structured， the initial point is searched out， and the projected points are orderly ranked according to the size of the polar angle. The data points are filtered and structured by using the constructed scanning line. The experimental results show that the scattered point cloud structuring method based on Denaunay triangularization and convex hull algorithm has short processing time， high stability and accuracy， and strong applicability， and can fully satisfy the excessive packaging detection system. In comparison with the current method， the method has better applicability， and can meet the needs of most platforms.

Keywords： excessive packaging； scattered point cloud； Graham scanning algorithm； Denaunay triangularization； convex hull algorithm； point cloud structuring

0 引 言

在過度包装检测的过程中，首先对商品和商品包装进行扫描，得到空间散乱点云[1?2]，完成空间重建；然后利用本文提出的方法对散乱点云进行结构化处理，明确拓扑信息；最后进行空隙率计算，得到是否过度包装的结论。所谓点云，是指在逆向工程中通过测量仪器得到的产品外观表面的点数据集合。由于获取方便、表示简单、灵活等优势、点云逐渐成为常用的三维模型表示方法[3]。点云数据通常会携带着坐标信息和其他拓扑信息，所以目前绝大多数的三维建模使用的都是点云数据。散乱点云指的是点与点之间的拓扑关系尚未明确的点云。

寻找拓扑关系是三维重建必不可少的过程，目前使用的是基于德劳内（Delaunay）[4?5]结构化方法和基于凸包[6?8]的结构化方法。基于德劳内三角化法的结构化处理中的逐点插入法是一个传统的方法，由于要花费大量的时间在点的查询及三角形的定位查询上，逐点插入法的时间复杂度较大，特别是如果每次查询插入点都是对整个点集里的所有点，则算法的时间复杂度将进一步增大。

基于Graham扫描法[9]是通过寻找一个起始点，对所有点与初始点形成的极角逆时针排序，利用压栈操作对外围的点存储和排序。凸包通常都是显示着物体的大致轮廓，且比实际的面积略微扩大，显然不适合处理体积大小的问题。

基于Graham扫描法改进型构造算法，兼容了上述两种方法的优点，避免了不足，为后面体积计算的实验数据精度提供了有力保障。

1 Graham扫描法

Graham扫描法[10]过程描述如下：

1） 在所有点中选取[y] 坐标最小的一点H，当作基点。如果存在多个点的[y]坐标都为最小值，则选取x坐标最小的一点。坐标相同的点应排除。然后按照其它各点[p]和基点构成的向量[]与x轴的夹角，根据夹角大小进行排序，进行顺时针的扫描，如果夹角从小到大排序则进行逆时针的扫描。最终求解过程中无需求出夹角大小，只需要根据余弦定理求出向量夹角的余弦值即可。图1中，基点为[H]，根据夹角的大小由小至大依次排序后为H，K，C，D，L，F，G，E，I，B，A，J，接下来进行逆时针的扫描。

2） 线段[]。该线段一定存在于凸包上，然后加入[C]。假定线段[]恰好也在凸包上，因为对[H]，[K]，[C]三点来说，凸包就是由这三点组成的。接下来给初始凸包加入[D]点时发现，此时线段[]才会在凸包上，然后将线段[]排除，所以[C]点不是凸包上的点。

3） 在加入一点时，必须首先考虑前面线段有没有出现在凸包上。扫描从基点处开始，凸包上的每条邻接线段的旋转方向相同，并且和扫描的方向应该相反。当发现新加入的点使新线段和上线段的转动方向发生了变化，便可以判定之前的点肯定没有在凸包上。实现时可用向量叉积进行判断，假设加入的一点为pn+1，之前点为pn，再上一点是pn -1。在进行顺时针扫描的时候，当向量与的叉积值为正（在逆时针扫描的时候判断恰好相反），此时把上一点删除。整个删除过程都要回溯，把之前计算出的全部叉积符号是相反的点全部删除，最后把新点加入到凸包。

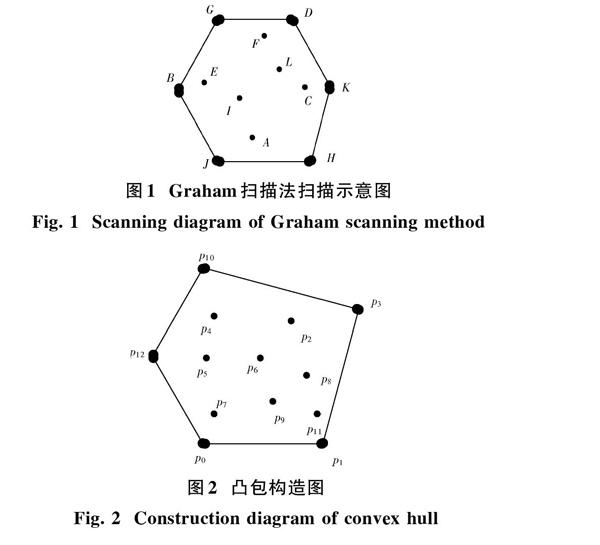
4） 在图1中，当加入[K]点时，由于[]需要旋转到[]时的角度是顺时针转动，所以[C]点确定不在凸包的边缘上，予以删除，但保留[K]点。然后继续加入[D]，因为线段[]要旋转到[]的角度，是逆时针转动，所以[D]保留。按照上面的步骤进行继续扫描，直到遍历所有的点即可。

图2中外围形状表示的多边形就是点集[Q]={p0， p1，…，p12}的凸包。

假设一个有三个或者以上点的点集[Q]，Graham扫描法的过程如下：

1） p0为[Q]中x?y坐标系下排序值最小的点；

2） 设S是对其余以p0点为中心的极角进行逆时针排序得到的点集；

3） p0进栈S；

4） p1进栈S；

5） p2进栈S；

6） 直至所有的点全部压入栈S；

7） 由S的栈顶元素和栈顶元素的下一个元素，和p1构成的折线只拐向右侧；

8） 对S弹栈；

9） 压pi进栈S；

10） 返回栈S。

经过上述过程的执行，栈S由栈底至栈顶元素就是[Q]凸包的顶点按照逆时针排序所得出的。在对点按极角大小按照逆时针来排序的时候，不需求出极角的值，只需要求出次序就可以。这个步骤通常可以使用矢量叉积性质实现。该算法在对二维点云进行结构化处理时，只可能出现凸多边形，而本文所研究的系统中物体轮廓会出现凹槽，這就导致在精度上该算法会出现一定的损失。

2 基于Graham扫描法改进型构造算法

针对存在的问题，提出了基于Delaunay三角化法和Graham扫描法的改进算法。基于Graham扫描法改进型构造算法流程如图3所示。

2.1 初始点的选择及构造扫描线

在所有的二维投影点数据中，分别搜索出点云水平方向的最小值和垂直方向上的最大值和最小值，构造包含所有点的正方形，初始点为两条对角线的交点，同时找出最左下方的点，记作p0，如图4所示。

构造包含所有点的最小包围盒，构造规则的包围盒，是为了在选择初始点的时候计算更加的方便，通过数据点中的几个最大最小目标点就可以确定初始点。

以该点为出发点，构造射线，以射线与x轴夹角为0时为初始扫描线，进行逆时针旋转扫描，如图5所示。

2.2 数据点的筛选排序和存储

对所有的点云数据点与初始点连线按照角度由小到大进行排序；假设坐标原点[o]，初始扫描线上的某点[pa] ，和数据点处于当前扫描线上的位置点[pb]。于是极角大小[A]为：

[A=（xpa-xo）×（ypb-yo）-（xpb-xo）（ypa-yo）] （1）

可以根据极角[A]的大小对所有点进行排序。

使用扫描线进行扫描，当同一角度的射线上含有2个或者含有2个以上的点，选择最外侧的点（可以用距离进行判断），只保留最外侧的点，将其余的点舍弃。

[pi=max（dis（o，pk））， i，k=1，2，3，…] （2）

[pi]为需要存储的点，[pk]为扫描线上的点。[dis（o，pk）]为求解距离函数，约简示意图如图6所示。

将筛选后的点一次进行压栈操作，便可以存储相互的拓扑信息。从A点开始，按照扫描线扫描的顺序依次连接筛选后的坐标点。结果如图7所示。

3 基于Graham扫描改进型算法的体积计算

在过度包装检测系统中，采用的是切片法来计算体积，对于每一个切片的投影需要进行二维层面的结构化处理。首先将商品的空间点云进行切割，然后对切片进行投影，其次对每一个切片投影进行结构化处理，再利用矢量乘法求得投影面积，最终求得体积。切片的大小直接影响着体积计算精度，切片越大，精度越低，切片越小，精度越高。

4 实验分析

实验物体是石膏制的维尼熊，瓦楞板纸箱和叮当猫，分别有41 000个，57 900个和35 200个数据点，通过对上述两种方法的测试得到以下数据。

4.1 处理时间比较

基于Graham扫描算法的改进型算法在和Graham扫描法在处理同样数据的情况下，改进型算法具有更短的运行时间。处理的时间如图8所示。

4.2 体积计算时间

在切片大小不变，数据点逐渐减小的基础上，对基于两种方法的体积计算运行时间进行比对，如图9所示。通过对规则轮廓（杯子外包装）和不规则轮廓（维尼熊艺术品）的体积计算验证基于Graham扫描算法和基于改进型构造算法的点云体积计算算法的计算精度、准确性和效率，通过实验，验证结果如表1所示。

5 结 语

本文提出了一种基于Graham扫描法的改进型点云体积构造算法。该算法是对已有的Graham扫描算法的有效补充和改进。该算法的关键在于对于初始点的选择，和对大量数据的预筛选。实验表明，改进型点云构造算法可以完全满足过度包装检测系统对计算体积的实时性和精度需求。与Graham扫描算法相比，该算法具有更高的精度同时拥有更短的运行时间。

注：本文通讯作者为张毅坤。

参考文献

[1] ZHANG X， LI G， ZHAO J， et al. New triangulation method for surface scattered points [C]// Proceedings of IEEE International Conference on Mechatronics and Automation. Tianjin： IEEE， 2014： 541?546.

[2] HE X， NI M， XUE Y， et al. An algorithm for topology reconstruction of scattered point cloud in reverse engineering [J]. Intelligent control and automation， 2010， 20（1）： 3126?3131.

[3] 王凯，支煜，张毅坤，等.一种检测摄像机与被测物间三维轴线求解方法[J].现代电子技术，2015，38（18）：22?25.

WANG Kai， ZHI Yu， ZHANG Yikun， et al. A method to calculate three?dimensional axis between detecting camera and object under test [J]. Modern electronics technique， 2015， 38（18）： 22?25.

[4] SONG D， LI Z. A fast surface reconstruction algorithm based on Delaunay [C]// Proceedings of International Conference on Computer Science and Information Processing. Xian： IEEE， 2012： 981?984.

[5] ZHAO M， AN B， WU Y， et al. A robust Delaunay triangulation matching for multispectral/multidate remote sensing image registration [J]. IEEE geoscience & remote sensing letters， 2015， 12（4）： 711?715.

[6] KLETTE G. A recursive algorithm for calculating the relative convex hull [C]// Proceedings of 25th International Conference of Image and Vision Computing. Queenstown： IEEE， 2010： 1?7.

[7] 刘人午，杨德宏，李燕，等.一种改进的最小凸包生成算法[J].大地测量与地球动力学，2011，31（3）：130?133.

LIU Renwu， YANG Dehong， LI Yan， et al. An improved algorithm for producing minimum convex hull [J]. Journal of geodesy and geodynamics， 2011， 31（3）： 130?133.

[8] LIU Guanghui， CHEN Chuanbo. A new algorithm for computing the convex hull of a planar point set [J]. Journal of Zhejiang University： Science A， 2007， 8（8）： 1210?1217.

[9] TERESHCHENKO V， TERESHCHENKO Y， KOTSUR D. Point triangulation using Graham′s scan [C]// Proceedings of 5th International Conference on the Innovative Computing Technology. Pontevedra： IEEE， 2015： 148?151.

[10] MAHMOOD M T， CHOI Y K， SHIM S O， et al. Estimating shape from focus by Gaussian process regression [C]// Proceedings of IEEE International Conference on Systems， Man， and Cybernetics. Seoul： IEEE， 2012： 1345?1350.