求解凸二次规划的连续型神经网络模型
2018-07-27杨静俐吴艺团陈锦奎
杨静俐,吴艺团,陈锦奎
(1.3.泉州信息工程学院 公共教学部,福建 泉州 362000;2.泉州市南安柳城中学,福建 泉州 362000)
0引言
二次规划是非线性规划的一种特殊类型,具有线性约束的二次规划问题广泛地出现在社会、经济、生产和经济计划等诸多应用领域[1-2]。 若考虑目标函数是二次的而约束条件是线性的情况,其一般形式为:
(1.1)
其中可行域Ω是Rn中的一个多面体,x=(x1,x2,…xn)T为n维决策变量,Hesse矩阵Q∈Rn×n是一个n×n的实对称矩阵,c∈Rn.该二次规划有许多方面的应用,如线性回归问题和序列二次规划问题。 二次规划现已成为组合优化、系统分析、经济数学、管理科学的基本方法。对二次规划问题的研究也引起了众多学者和专业人员的广泛兴趣[3-9]。
众所周知,人工神经网络是由大量简单的基本元件——神经元相互连接,通过模拟人的大脑神经处理信息的方式,进行信息并行处理和非线性转换的复杂网络系统。由于神经网络具有强大的学习功能,同时具有平行与分布式特征,可以轻松地实现非线性映射过程,并且具有大规模并行计算能力。 因此,神经网络方法为优化问题的计算提供了一条新的途径,并已成为求解最优化问题的重要方法之一。1984年,Hopfield把离散型神经网络进一步发展成连续型神经网络[10-11],连续型神经网络基本结构与离散型神经网络的基本结构相似,但连续型神经网络中所有神经元都同步工作,各输入-输出量均是随时间连续变化的模拟量,这就使得连续型神经网络比离散型神经网络在信息处理的并行性、实时性等方面更接近于实际生物神经网络的工作机理。本文设计的连续型神经网络模型,网络规模为3n,同时不含任何参数变量,全局指数稳定,复杂度仅仅依赖于目标函数。
1 连续型神经网络模型
为了导出结论,本节先介绍以下定义和引理。
定义 2.1[12]令Ω⊂Rn是闭凸集,若∀x∈Rn,存在唯一的点y∈Ω,使得
‖x-y‖≤‖x-z‖(∀z∈Ω).
则称y为x在集合Ω上的投影,记:y=PΩ(x)=argminz∈Ω‖x-z‖.
定义 2.2[12]令Ω⊂Rn是闭凸集,连续函数F:Rn→Rn,变分不等式VI(F,Ω)是寻找x*∈Ω,使得
(x-x*)F(x*)≥0 ∀x∈Ω.
引理 2.1[12]令x*是优化问题
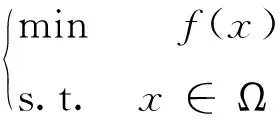
(2.1)
的解,其中Ω⊂Rn是闭凸集,f是连续可微函数,那么x*也是变分不等式▽f(x*)T(x-x*)≥0(∀x∈Ω)的解。
引理 2.2[12]若f是连续可微函数,x*是变分不等式VI(▽f,Ω)的解,则x*也是优化问题(2.1)的解。
定义 2.3[12]令U:Rn→Rn,非线性互补问题(NCP)是指寻找x∈Rn,x≥0,使得下列等式和不等式成立:
U(x)≥0
U(x)Tx=0
(2.2)
若U(x)是仿射的,即U(x)=Mx+q,其中M是矩阵,q是向量,则(2.2)为线性互补问题(LCP)。
定义 2.4[12]混合非线性互补问题(MNCP)是指寻找x∈Rn,使得下列等式和不等式成立:
Uixi=0,
Ui≥0,xi≥0,i∈I
(2.3)
Uj=0j∈L-I,
其中U是Rn→Rn的可微映射,L={1,2,…,n},I⊂L.若U是仿射的,即U(x)=Mx+q,其中M是矩阵,q是向量,则(2.3)为混合线性互补问题(MLCP)。
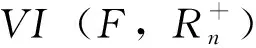
引理 2.4[12](投影定理)令Ω⊂Rn是闭凸集,则x*∈Ω是变分不等式VI(F,Ω)的解,当且仅当对∀α>0,x*是映射PΩ(I-αF):Ω→Ω的不动点,即x*=PΩ(x*-αF(x*)).
引理 2.5[12]令Ω⊂Rn是闭凸集,则下面两个不等式成立。
(1)(v-PΩ(v))T(PΩ(v)-u)≥0,∀v∈Rn,u∈Ω;
(2)‖PΩ(u)-PΩ(v)‖≤‖u-v‖,∀u,v∈Rn.
由引理2.1、引理2.2和引理2.3,我们可以得出如下结论:
定理 2.1x*∈Rn是问题(1.1)的最优解,当且仅当存在y*∈Rn使得
证明 根据Kuhn-Tucker条件和引理2.1、引理2.2和引理2.3,定理即可证明。
根据定理2.1和引理2.5,优化问题(1.1)的解就是下面投影方程的解,即
PΩ(Dx-(Bx+d))=Dx
(2.4)
其中B=D-TA,d=-D-Tc.
根据上述预备知识,本文构造如下两个连续型神经网络模型用于求解问题(1.1),其中神经网络(2.5)为直接神经网络,其平衡点即为问题(1.1)的最优解;令问题(1.1)中y=Dx,即可得到间接神经网络(2.6),从而y为神经网络的平衡点,D-1y为问题(1.1)的最优解。
直接神经网络模型:
(2.5)
其中PΩ(x)=「PΩ(x1),PΩ(x2),…,PΩ(xn)⎤T,B=D-TA,d=-D-Tc,同时,投影算子PΩ(xi)为具有如下形式的分段函数
间接神经网络模型:
(2.6)
其中,W=D-TAD-1,q=D-Tc.
易知,神经网络(2.5)包含2个隐含层,神经网络(2.6)只包含1个隐含层,且这两个神经网络模型均可以用硬件实现,其电路实现优简单的加法器、放大器、n个用来实现▽f(x)的处理器和n积分器以及分段线性激励函数PΩ(·)来实现。下文对神经网络(2.5)、(2.6)的稳定性进行讨论。
2 稳定性分析
本节首先给出稳定性的相关定义。
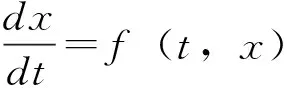
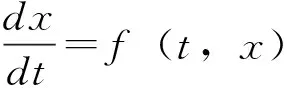
‖x(t)-x*‖≤k(δ)‖x(t0)-x*‖e-λ(t-t0),∀t≥t0.
对于神经网络(2.5),有如下稳定性定理。
定理 3.1 若A是半正定矩阵,则神经网络(2.5)是Lyapunov意义下稳定的,且全局收敛到问题(1.1)的最优解。若A是正定矩阵,则神经网络(2.5)全局指数收敛到问题(1.1)的唯一的最优解。
证明 令x*是问题(1.1)的最优解,由引理2.5知,
{PΩ[Dx-(D-TAx-D-Tc)]-Dx*}T{PΩ[Dx-(D-TAx-D-Tc)]-[Dx-(D-TAx-D-Tc)]}≥0
则
(x*-x)TD{PΩ[Dx-(D-TAx-d)]-Dx}+(x-x*)TAD-1{PΩ[Dx-(D-TAx-d)]-Dx}≥‖PΩ[Dx-(D-TAx-d)]-Dx‖2+(x-x*)TA(x-x*)
取Lyapunov函数
则有
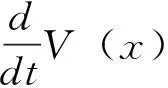
≤0
所以神经网络(2.5)是Lyapunov意义下稳定的且全局收敛到问题(1.1)的最优解。
若A是正定矩阵,则有
即
V(x)≤V(x0)e-2μ(t-t0)
从而
‖x(t)-x*‖≤‖x(t0)-x*‖e-2μ1(t-t0)(μ1>0)
即证明神经网络(2.5)全局指数收敛到平衡点。
定理 3.2 对每一个y∈Rn,神经网络(2.6)在区间[t0,+∞]上存在唯一的、连续的解y(t),且y(t0)=y0.
证明 令T(y)=PΩ(y-(Wy+q))-y,对∀y,v∈Rn,有:
‖T(y)-T(v)‖=‖PΩ(y-(Wy+q))-y-PΩ(v-(Wv+q))+v‖
≤‖PΩ(y-Wy-q)-PΩ(v-Wv-q)‖+‖y-v‖
≤2‖y-v‖+‖W‖‖y-v‖
≤(2+‖W‖)‖y-v‖
这表明T(y)满足Lipschitz条件,由解的存在唯一性定理知,对∀y∈Rn,神经网络(2.6)有唯一的连续解y(t),且y(t0)=y0.
对于神经网络(2.6),有如下稳定性定理。
定理 3.3 若A是半正定矩阵,则神经网络(2.6)是Lyapunov意义下稳定的,且全局收敛到平衡点y*,同时D-1y*是问题(1.1)的最优解。若A是正定矩阵,则神经网络(2.6)全局指数收敛到平衡点y*,同时D-1y*是问题(1.1)的唯一的最优解。
证明 定义F(y)=PΩ(y-(Wy+q))-y.
显然,F(y)=0当且仅当y是投影方程(2.4)的解,这样神经网络(2.6)的平衡点对应于(2.4)的解,而投影方程(2.4)的解对应于二次规划问题(1.1)的解。首先,令y=Dx,则二次规划问题(1.1)可以写成如下形式:
(3.1)
其中W=D-TAD,q=D-Tc.显然,若y*是问题(3.1)的最优解,则D-1y*是问题(1.1)的最优解。 同时,W是对称半正定的,若A是正定矩阵,则W也是正定矩阵。由定理2.3知神经网络(2.6)对任意的初始点均有唯一的连续解y(t).根据引理2.5,对∀y∈Rn,v∈Ω,有
[v-PΩ(y-(Wy+q))]T[PΩ(y-(Wy+q))-(y-(Wy+q))]≥0.
(3.2)
由于y*是投影方程(2.4)的解,对∀v∈Ω,有
(v-y*)T(Wy*+q)≥0
(3.3)
在(3.1)式中令v=y*,在(3.3)式中令v=PΩ(y-(Wy+q)),然后把两个不等式相加,得到
[y*-PΩ(y-(Wy+q))]T[W(y-y*)-y+PΩ(y-(Wy+q))]≥0.
将上式进行整理,得
即
取Lyapunov函数
其中y*是问题(3.1)的最优解,M2=(I+W)且M是对称正定矩阵。 则
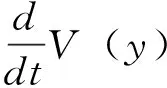
=(y-y*)TMTMPΩ((y-(Wy-q)-y)
≤0
所以神经网络(2.6)是Lyapunov意义下稳定的且全局收敛到问题(1.1)的最优解。
若A是正定矩阵,则有
(y-y*)TW(y-y*)≥δ‖y-y*‖2(δ>0).
因此
即
V(y)≤V(y0)e-2δ(t-t0)
从而
‖y(t)-y*‖≤‖y(t0)-y*)‖e-2δ1(t-t0)(δ1>0)
即证明神经网络(2.6)全局指数收敛到平衡点。
3数值试验
本节构造如下测试问题,以验证所提出算法的有效性能。
例1 考虑如下具有线性约束的二次规划问题
则
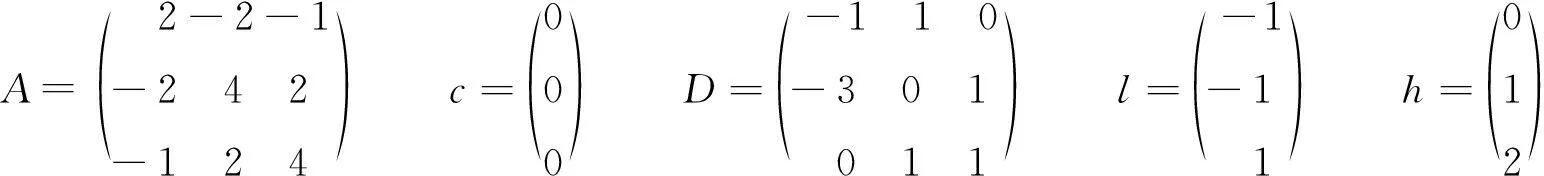
此问题的最优解x*=[0.5,0.5,0.5]T.
分别用本文构造的连续型神经网络(2.5)和(2.6)求解该问题。初始输入均取为[-1.5,0,1.5]T,模拟结果表明神经网络(2.5)总收敛于二次规划问题的最优解,神经网络(2.6)收敛于其平衡点y*=(0,-1,1)T(y*=Dx*).神经网络(2.5)的轨迹状态如图4.1。
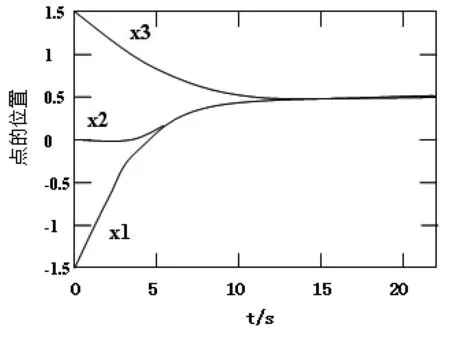
图4.1 神经网络(2.5)的轨迹状态
神经网络(2.6)的轨迹状态如图4.2。
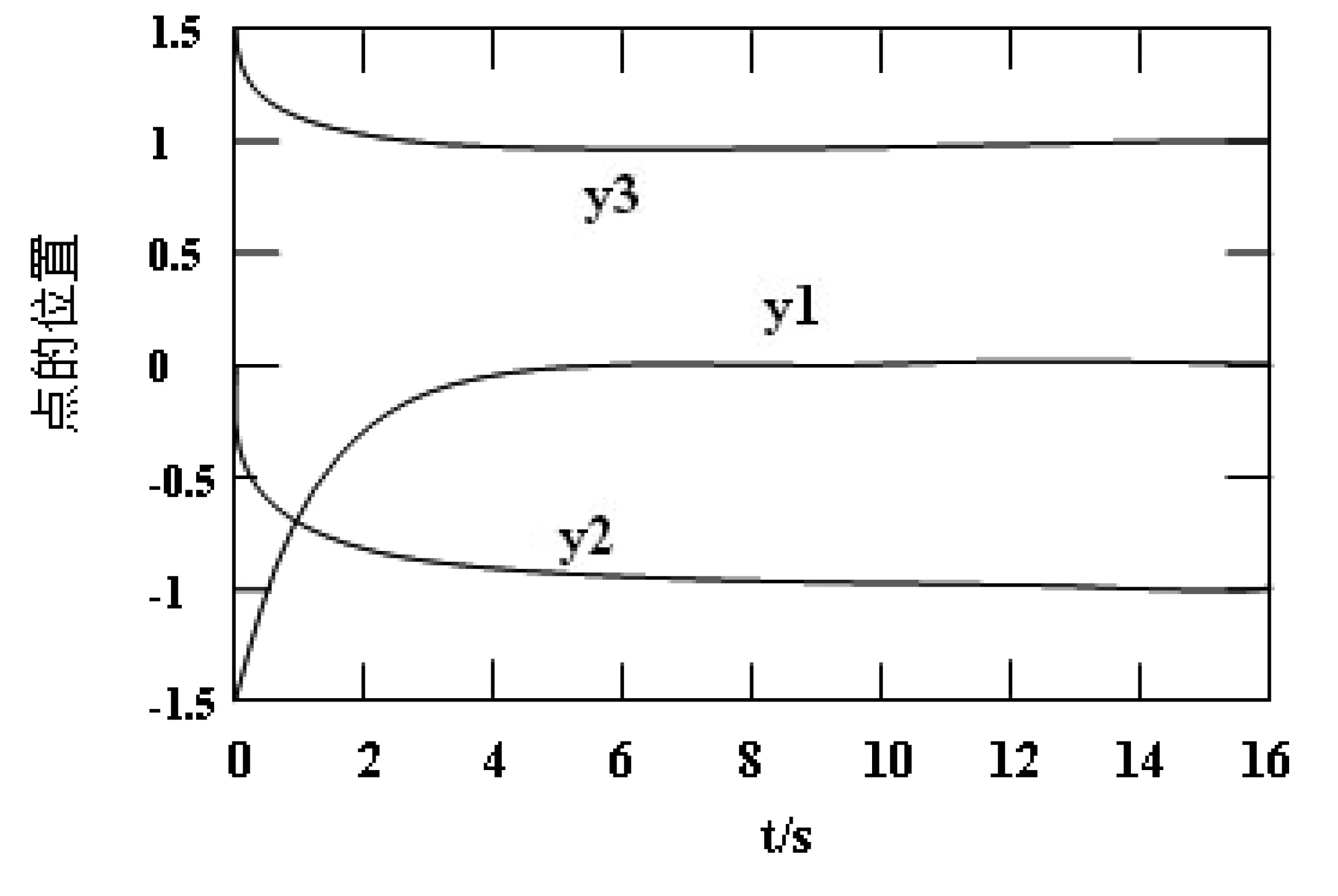
图4.2 经网络(2.6)的轨迹状态
4小结
本文构造连续型神经网络求解凸二次规划问题,模型不含任何参数,算法简单,复杂度仅依赖于目标函数,且是全局指数稳定的,为凸二次规划问题的求解提供了一种有效途径。
