可向特定负荷定时限独立供电的储能系统优化配置

孙 鸣, 桂 旭

(教育部光伏系统工程研究中心(合肥工业大学), 安徽省合肥市 230009)

0 引言

在新能源发电密集接入区,存在着新能源发电有较强的随机性和间歇性的问题[1-2],多能互补及配备储能设备可以有效解决这一问题。储能系统的合理配置可以起到消纳新能源过剩发电[3]、平抑新能源发电波动、改善电能质量、削峰填谷等作用[4-5],并可在多能互补装置运行区域发生非计划停电,形成孤网时提供一定时长的紧急功率支撑。因此,合理配置的储能设备可作为多能互补分布式能源综合利用的有效补充和保障。

目前,储能技术主要分为机械储能、蓄电池储能、电磁储能和热力储能4类[6],蓄电池储能系统(battery energy storage system,BESS)具有效率高、寿命长、使用方便等优点,因而受到更多的关注和研究。在新能源发电装置密集接入区域,如何通过合理规划BESS的方式,实现多能互补装置运行区域发生非计划停电时,在满足向特定负荷独立供电一定时长的需求下,同时实现经济效益最大化是多能互补、集成优化能源系统关键技术中必不可少的一环。

文献[7-8]从规模储能装置的性能指标和运行经济指标出发,给出了储能装置的广义经济效益指数,但未给出特定领域中的经济收益指标。文献[9]针对国外电网提出了一种储能电池的经济效益模型,该模型没有涉及在网损方面的经济效益。文献[10]建立了以每天的净现值收益为目标函数的储能系统经济性评估数学模型,由于用户更关注年投资回报率,净收益高未必能反映储能系统的投资回报效率。文献[11-12]建立了以全寿命周期内净收益最大为目标函数的经济性评估的数学模型,但未考虑放电深度(depth of discharge,DOD)和电池寿命的关系对经济效益及最优配置的影响。

针对上述现状,本文以保证供电区域内重要负荷在一定时限内独立供电为前提,以在配电网中的BESS全寿命周期内的年投资回报率最大为目标,研究储能系统的最优配置。论文建立了包括蓄电池全寿命周期内“低储高发”的套利收入在内的4项收益指标和全寿命周期成本的经济效益模型,提出了一种通过提取关键影响因子逐步简化优化模型的方法。通过算例分析比较不同电池在保证特定负荷在一定时限内独立供电的储能配置和年投资回报率,并给出最优配置方案的建议,验证了所建模型和求解方法的可行性。

1 蓄电池的对比分析

由于蓄电池种类很多,本文选取了铅炭电池(Pb-C battery,PCB)、磷酸铁锂电池(lithium iron phosphate battery,LFP)和梯次电池这3种前景较好的蓄电池作为储能配置和经济性分析的研究对象。三种蓄电池的性能对比见附录A表A1。

由附录A表A1可以看出,PCB循环性好,成本低,可回收,寿命较传统的铅酸电池有了大幅度提升,但其能量密度低,对场地要求高;LFP环保、单体电压高、能量密度较大、循环寿命也已经达到了一定水平,但成本较高,不耐过充过放,安全性有待提高。本文研究的梯次电池是从电动汽车上退役的LFP,梯次电池用于BESS相较于新电池未出现加速衰减的迹象[13],但当电池容量衰减至额定容量的80%以下时,动力电池就不适于应用在电动汽车上。如果直接将电池淘汰,必将造成资源的严重浪费,同时也会导致环境污染,梯次电池的提出使得大量的退役动力电池有了二次生命,应用在大规模储能中可以降低初期投资成本,提高资源的再利用率,减少环境污染。

2 全寿命周期内储能系统经济评价指标与模型

2.1 全寿命周期内储能系统经济效益评价指标

1)满足特定负荷1 h独立供电前提下的“低储高发”套利

本文将定时限选为“1 h”,以“1 h独立供电”为时长基准,对BESS配置进行定量规划。工程中若需向特定负荷设定不同的独立供电时长,均可参照文中的方法进行规划。选定“1 h”的参考依据为南方电网公司的相关规定:故障时间小于5 min,则视为轻型事故;故障时间大于5 min,小于15 min,则视为一般事故;大于15 min的,为重大事故[14]。电力故障通常为轻型事故和一般事故,在这两种事故发生时,“1 h独立供电”可提供45 min以上的故障处置和恢复供电的时间,故45 min的时间大概率可以恢复供电。

本文根据峰谷电价表,在夜晚低谷电价期间对BESS充电,第二天在确保可对余下时间段的负荷峰值独立供电1 h所需的电量的前提下,BESS将适时地在峰值电价时段卖出多余的存储电量。相应的全寿命周期内的收益为:

(1)

2)减少用户配电站建设容量指标

用电大户通常会配备具有一定冗余度的配电系统,在用户低压侧安装BESS可降低配电容量[15],节省相应的容量投资。这部分收益为:

(2)

式中:Pc=Pimax-Pa，为拉平负荷曲线所需功率，其中Pimax为日负荷峰值，Pa为负荷的日平均功率；Cd为用户配电系统的单位造价;γd为用户配电设备的固定资产折旧率;Pmax为BESS最大充放电功率,即额定功率。

3)提高供电可靠性指标

电力系统可靠性不足会对用户造成缺电损失,BESS提高了供电可靠性,减少了停电所带来的损失。相应的收益为:

(3)

式中:As为系统平均年停电率;RIEA为用户缺电损失评价率[16];EREC为BESS剩余电量期望值。

4)降低电网网损指标

蓄电池充电时相当于增加了系统负荷,增加了网损;放电时相当于减少了系统传输的功率,降低了负载率,减少了网损。降低网损带来的收益为:

(4)

式中:ΔPH为蓄电池放电时减少的有功功率损耗;ΔPl为蓄电池充电时增加的有功功率损耗。

2.2 储能系统成本模型

储能装置的投资成本[17]主要包括储能装置的固定投资成本和运行维护成本。

1)固定投资成本

固定投资成本与蓄电池的额定容量和额定充/放电功率有关[18],这部分的投资成本为[19]:

(5)

2)运行维护成本

这部分费用主要由BESS规模确定,可表示为:

(6)

式中:C2为BESS全寿命周期内的运行维护成本;Cm为BESS循环运行时年单位充/放电功率维护成本。

3 储能系统经济效益模型的建立与优化

3.1 储能系统经济效益评价模型的建立

由于不同种类的蓄电池在寿命、充放电效率、成本等方面存在较大差异,仅仅考虑到全寿命周期内成本最小或净收益最大比较片面,故本文考虑将BESS全寿命周期内的年投资回报率作为经济效益评价的数学模型,其模型为:

(7)

EY=EY1+EY2+EY3+EY4

(8)

CY=C1+C2

(9)

式中:Ryear为BESS年投资回报率;EY为BESS全寿命周期内的总收益;CY为BESS全寿命周期内的总投资成本。

3.2 储能系统经济效益评价模型的优化

以BESS全寿命周期内总的年投资回报率最大为目标函数,对比各类电池在保证特定负荷1 h独立供电下全寿命周期内的年投资回报率,从而选择出合适的电池类型和最优配置,即

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

式(11)为一天内储能电池充放电电量平衡约束;式(12)为最大放电量约束,t取1 h;式(13)为充放电功率约束; 式(14)为储能系统额定功率约束,其中Pload(i)为第i小时段的负荷功率;式(15)为保证特定负荷1 h独立供电下i时刻储能电池内所剩电量约束,t取1 h;式(16)为每天按给定的充放电深度放完电后剩余电量的约束,t取1h,Pnmax为BESS停止放电后晚间负荷最大值。上述各式中,式(11)至式(16)为约束条件,式(17)为充放电效率和放电深度的边界条件。

可向特定负荷独立供电1 h的BESS规划不同于传统的储能规划,既要满足1 h独立供电的要求,又要寻求经济效益最大。因此,BESS功率、容量及正常工作日DOD的规划有着更为严格的要求:①BESS功率/容量需不小于特定负荷峰荷1 h独立供电所需的功率/电量;②每个工作日BESS放电结束后剩余电量需不小于夜晚负荷最大值1 h独立供电所需电量;③满足①和②条件下,分析各类蓄电池不同DOD所对应的BESS配置方案,逐步简化优化模型,最终找到满足条件的最优配置。

由式(11)至式(14)可知,BESS充放电功率不能小于特定负荷峰值功率,考虑到留有10%的安全裕量,BESS功率配置最小取1.1Pimax;由式(15)和式(16)可知,储能容量配置不能低于两式中的最大值,以保证可对特定负荷独立供电1 h的需求,再考虑到留有10%的负荷增长空间,故式(15)和式(16)可改写为:

(18)

考虑以下两种情况。

满足条件的BESS最小功率/容量配置为:

(19)

经济效益模型中的相关参数见附录A表A2。将式(19)及附录A表A2中各参数代入式(1)至式(7),可得BESS全寿命周期内的收益、成本及年投资回报率，即

(20)

对于特定负荷,BESS最优配置由负荷峰值和储能充放电效率唯一确定;DOD由负荷峰值和晚间负荷最大值确定;年投资回报率也唯一确定。

满足条件的BESS最小功率/容量配置为:

(21)

将式(21)及附录A表A2中各参数代入式(1)至式(7),可得BESS全寿命周期内的收益、成本及年投资回报率，即

(22)

对于特定负荷,BESS配置和经济效益模型中存在D这一变量,通过分析各DOD下的最优配置及其年投资回报率,得到符合条件的储能配置。

4 算例分析

4.1 算例背景

图1为安徽省某市经济开发区西区医院及宾馆夏季典型工作日负荷曲线示意图(该类负荷在夏季峰值较其他季节为大,且夏季更易出现电力故障)。根据负荷曲线的特征,峰荷PH出现在15:00至18:00,其值为1.79 MW;22:00至次日07:00负荷最大值Pnmax为0.81 MW。

图1 典型工作日负荷曲线Fig.1 Load curve on typical workday

西区各时段用户的分时电价见附录A图A1。由附录A图A1可知,分时电价谷时段为每天23:00至次日07:00(谷电价为0.050 5万元/(MW·h))。对应图1可知,这段时间为用电负荷低谷,故BESS在这段时间内持续充电;同理,分时电价高峰时段为每天09:00至12:00,17:00至22:00两个时段(峰电价为0.121 5万元/(MW·h))。对应图1可知,这两个时段内为用电高峰期,其中峰荷出现在15:00至18:00。为始终保证这一区域内负荷独立供电1 h并实现最大的经济效益,峰荷到来前BESS始终留有可供峰荷1 h独立供电所需的电量,多余电能BESS将适时地在峰值电价时段卖出,即18:00过后BESS在峰值电价时段内开始逐渐放电,持续到22:00结束,此时BESS内剩余电量需不小于可向下一时段负荷独立供电1 h所需的电量,并持续充电到次日07:00。BESS充放电时间示意图如图2所示。

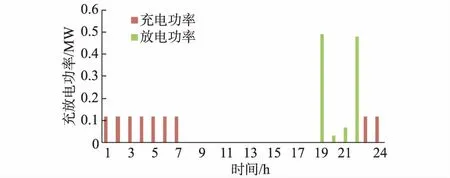
图2 BESS充放电时间示意图Fig.2 Charging/discharging time curves of BESS

依据以上分析,本文选择PCB,LFP和梯次电池这3种储能电池,3种蓄电池成本参数见附录A表A3。在保证区域内负荷独立供电1 h前提下,运用所提出的模型和分析方法,分析比较不同蓄电池的最优配置,得出在当前市场电价水平和成本下的年投资回报率。

4.2 蓄电池的最优配置

4.2.1PCB

根据式(11)至式(14),BESS功率配置需不低于峰荷功率1.79 MW,考虑到留有10%的安全裕量,BESS额定功率取2 MW满足要求。

根据PCB相关参数,由式(18)所确定的BESS容量下限关系式可写为:

(23)

(24)

考虑以下两种情况。

1)EP1≥EP2

PCB储能系统满足供电区域内负荷1 h独立供电要求的最小容量配置方案为2 MW/2.32 MW·h,实际工程中配置取2 MW/2.4 MW·h,工作日平均DOD为50%(DOD低于50%所对应的最小容量配置不满足最大负荷需求),某型号PCB在DOD为50%时全寿命周期循环次数为3 900次。

将相关参数及容量配置方案代入式(20)可以得到全寿命周期内总收益为635.4万元,总成本为471.7万元,净收益为163.7万元,年投资回报率约为3.5%,在寿命周期内第8年开始盈利(注:整流/逆变设备一般寿命在15年,大于所列蓄电池寿命,在进行经济性计算时不需追加二次投资)。

2)EP1

储能额定容量最小配置值用EP2表达式为:

(25)

s.t. 60%≤D<100%

(26)

式中:D值小于100%表示BESS不能完全充放电,要留有确保晚间负荷1 h独立供电的电量。

根据式(22)得到简化后仅含DOD和循环寿命两个变量的PCB储能系统年投资回报率表达式为:

100%

(27)

某型号PCB储能系统在负荷1 h独立供电的典型工作日,不同DOD下的最小配置如下。

①当DOD为60%时,全寿命周期内充放电循环3 000次,储能系统配置为2 MW/2.7 MW·h。

②当DOD为70%时,全寿命周期内充放电循环2 300次,储能系统配置为2 MW/3.5 MW·h。

③当DOD为80%时,全寿命周期内充放电循环1 800次,储能系统配置为2 MW/5.3 MW·h。

④当DOD为90%时,全寿命周期内充放电循环1 300次,储能系统配置为2 MW/10.5 MW·h。

PCB储能系统全寿命周期内的总收益、总成本、净收益及年投资回报率等经济数据见表1。

表1 PCB储能系统不同配置下的经济数据Table 1 Economic data of PCB under different configurations

综上,满足可向某市经济开发区西区医院及宾馆独立供电1 h的PCB储能系统在以下3种配置时可实现盈利:①2 MW/2.4 MW·h,DOD为50%;②2 MW/2.7 MW·h,DOD为60%;③2 MW/3.5 MW·h,DOD为70%。以上3种配置中,配置①的容量配置最小,投资成本最小,年投资回报率最高,故PCB储能系统配置为2 MW/2.4 MW·h,DOD为50%。

4.2.2LFP

根据LFP相关参数,由式(18)所确定的储能系统容量下限关系式为:

(28)

(29)

讨论两种情况,方法与PCB相同,得到符合条件的LFP储能系统配置方案如下。

①当DOD为50%时,全寿命周期内充放电循环5 000次,储能系统配置为2 MW/2.2 MW·h。

②当DOD为60%时,全寿命周期内充放电循环4 000次,储能系统配置为2 MW/2.5 MW·h。

③当DOD为70%时,全寿命周期内充放电循环3 200次,储能系统配置为2 MW/3.3 MW·h。

④当DOD为80%时,全寿命周期内充放电循环2 500次,储能系统配置为2 MW/5.0 MW·h。

⑤当DOD为90%时,全寿命周期内充放电循环2 100次,储能系统配置为2 MW/9.9 MW·h。

LFP储能系统年投资回报率表达式为:

(30)

LFP储能系统全寿命周期内的总收益、总成本、净收益及年投资回报率等经济数据如表2所示。

表2 LFP储能系统不同配置下的经济数据Table 2 Economic data of LFP under different configurations

综上,满足向某市经济开发区西区医院及宾馆独立供电1 h的LFP储能系统在以下4种配置时可实现盈利:①2 MW/2.2 MW·h,DOD为50%;②2 MW/2.5 MW·h,DOD为60%;③2 MW/3.3 MW·h,DOD为70%;④2 MW/5.0 MW·h,DOD为80%。4种配置中,配置①的容量配置和投资成本均较小,年投资回报率较高,故LFP储能系统配置为2 MW/2.2 MW·h,DOD为50%。

4.2.3梯次电池

梯次利用的LFP在容量配置和经济性计算时有以下特点。

①本例选用的梯次电池可利用容量为新电池额定容量的80%,在BESS配置过程中需多配置一些容量以满足负荷需求。

②对梯次电池储能系统进行成本分析时除了电池的固定投资成本和运行维护成本,还要对电池进行检测、筛选、重新配组,由此产生了筛选配组成本,这部分成本为5万元/(MW·h)。

③梯次电池寿命通常较新电池短,而整流/逆变设备寿命较长(一般可达15年),在进行经济性分析时,为了充分利用整流/逆变设备及分析长期的经济效益,考虑二次投资即更换一次电池,更换成本为5万元/(MW·h)。

根据梯次动力电池相关参数,由式(18)所确定的BESS容量下限关系式为:

(31)

(32)

讨论两种情况,同理,得到符合条件的梯次利用的LFP储能系统配置方案如下。

①当DOD为50%时,全寿命周期内充放电循环2 600次,储能系统配置为2 MW/2.8 MW·h。

②当DOD为60%时,全寿命周期内充放电循环2 000次,储能系统配置为2 MW/3.1 MW·h。

③当DOD为70%时,全寿命周期内充放电循环1 500次,储能系统配置为2 MW/4.2 MW·h。

④当DOD为80%时,全寿命周期内充放电循环1 100次,储能系统配置为2 MW/6.2 MW·h。

⑤当DOD为90%时,全寿命周期内充放电循环900次,储能系统配置为2 MW/12.4 MW·h。

梯次电池储能系统初期固定投资成本为:

(33)

梯次电池储能系统更换电池的二次固定投资成本为:

(34)

年投资回报率表达式如下:

(35)

梯次电池储能系统在更换一次电池后全寿命周期内的总收益、总成本、净收益及年投资回报率等经济数据如表3所示。

表3 梯次电池储能系统不同配置下的经济数据Table 3 Economic data of second-use battery under different configurations

综上,满足可向某市经济开发区西区医院及宾馆独立供电1 h的梯次电池储能系统在以下两种配置时可实现盈利:①2 MW/2.8 MW·h,DOD为50%;②2 MW/3.1 MW·h,DOD为60%。两种配置中,配置①的容量配置和投资成本均较小,年投资回报率较高,故LFP储能系统配置为2 MW/2.6 MW·h,DOD为50%。

4.3 年投资回报率的分析

随着DOD的递增,需配置的储能容量随之增大,寿命随之减小,容量增大使得收益和投资成本都上升,寿命的减小又降低了全寿命周期内的收益,所以BESS的年投资回报率函数是一个复杂函数。分析式(20)、式(22)、式(27)、式(30)和式(35)可知,BESS的投资回报率主要取决于DOD变化时循环次数增减幅度的大小,在一定范围内,DOD每降低10%,循环次数增幅越大时,所带来的收益增长速率会超过投资成本增长速率,投资回报率由负变正并逐渐增加。由式(20)得到DOD的下限取决于负荷峰值和晚间负荷最大值,对特定负荷来说,这个值是定值,就本文而言这个值是50%,与BESS电池种类无关,只和负荷特性有关。

4.4 算例小结

通过对三种电池的最优配置及对应的全寿命周期内的经济效益分析,可以得到如下结论:①总的净收益方面,梯次电池、LFP,PCB依次增加;②一次投资成本方面,梯次电池、PCB,LFP依次增加;③总投资成本方面,PCB,LFP、梯次电池依次增加;④年投资回报率方面,梯次电池、LFP,PCB依次增加。就本例而言,BESS配置中经济效益最好的是PCB,而LFP循环寿命更长、性能更优且经济效益随着电池价格的迅速下降将会有大幅度提升,这两种电池都适用于本例储能系统;梯次电池虽然初期投资最小,但目前来看BESS全寿命周期内总成本较大,经济效益不显著,不适用于本例中的储能系统。

5 结语

本文的主要结论如下。

1)在BESS优化配置过程中通过寻找影响储能配置的关键因素,逐步简化数学模型,避免了繁琐的寻优过程,更具工程实用性。

2)PCB前期投资较小,投资的年回报率较高,但存在碳污染的隐患,目前对于大规模的储能系统,使用PCB经济效益更好;LFP环保、充放电效率高、寿命长、可大倍率充放,但目前成本依然较高,经济效益不显著,随着近几年LFP价格的快速下降,其应用在BESS的年投资回报率会有明显上升;梯次电池提高了电池的再利用率,缓解了电池处理中的污染问题,应用在储能方面可以降低初期投资成本,但目前在BESS中使用梯次电池全寿命周期内的总成本较高,年投资回报率较低,经济效益不明显。

3)目前BESS的年投资回报率随着近几年电池价格的迅速下降已经有了大幅提高,峰谷电价差越大的地区BESS的经济效益越好。BESS大规模应用的关键在于蓄电池循环寿命的提高、充放电效率的提升、成本的下降及商业模式的完善和政策的支持。

本文在计算过程中未考虑蓄电池容量衰减等因素对计算结果的影响,且经济效益的影响因素考虑也不够全面。故如何更加全面地考虑各方面因素以实现储能系统优化配置有待进一步研究。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。