热网特性对于综合能源系统超短期调度的影响

姚 帅, 顾 伟, 张雪松, 赵 波, 陆 帅, 吴晨雨

(1. 东南大学电气工程学院, 江苏省南京市 210096; 2. 国网浙江省电力公司电力科学研究院, 浙江省杭州市 310014)

0 引言

随着世界能源危机和环境污染问题的日益加重,能源互联网、综合能源系统、“互联网+”智慧能源等创新想法不断涌现[1-3],转变能源供给模式,建设清洁高效的现代能源体系具有重要意义。综合能源系统依托能源传输技术、能量转换设备和可再生能源等相关技术的不断革新,耦合电网、热网和天然气网等多种能源网络,有利于实现多能协同供应和能源综合梯级利用,逐渐成为能源领域的重要发展趋势之一[4-7]。

多种能源相互耦合是综合能源系统区别于传统能源系统的重要标志之一[1],各类能源的特性差异对系统的规划运行提出了新的挑战。区域热网作为传输热能的媒介,由于在传输损耗和传输时延方面与电网具有明显差异[5-7],在构建多能协同供应的综合能源系统中吸引了广泛的研究关注。文献[6]针对多区域综合能源系统之间的环状热网,考虑了网络流量—温度约束和热损平衡约束,并将其应用于多区域综合能源系统的协同规划。文献[8]关注区域热网的传输时延,提出了一种利用热网和建筑物负荷的热惯性来消纳风电的优化运行模型。文献[9-12]采用相似的思路,利用区域热网的蓄热能力适应大量的可再生能源接入,提高系统运行的灵活性和经济性。

目前对于热网水力工况的研究已趋于成熟,但对热力工况的研究尚处于探索阶段[13-14]。文献[10]提出了一种分开考虑输送延迟和热损失的方法来模拟热网温度变化的动态特性。文献[15]对热网进行动态仿真,通过改变热源供热量,定量分析了管网的输送延迟和蓄热特性。文献[16]在节点法的基础上提出了一种突出考虑热网暂态温度特性的数值模拟方法,并与商业软件TERMIS的预测结果进行对比。

上述研究虽然能够获得较高精度的热力数据,但是所用模型较为复杂,求解耗时长,并且需要给定用户热负荷数据和热源供水温度,难以应用于综合能源系统的超短期调度中。部分学者面向稳态传热问题,对热网的传热特性和网络约束做了大量简化。文献[6]中所建立的热网模型未考虑管段的温度、压力变化和传输延时特性。文献[7]固定回水温度,未考虑回水管网拓扑结构和温度变化对于供热系统的影响。文献[17]认为热网中热媒的出口温度跟随入口温度实时变化,忽略了热媒温度由初态变化到稳态的过渡过程。上述热网模型虽然易于求解,但是当系统调度策略的时间尺度与热网延时相当时,将导致显著的误差,因而问题的关键在于建立一个兼顾精确性和求解复杂度的热网模型。

本文在现有热网模型的基础上,进一步考虑回水管网的拓扑结构、管段温度变化的暂态过程和热网传热的时延特性,建立精细化的热网模型,兼顾了模型精确性和求解复杂度。为了反映热网特性对于综合能源系统超短期调度策略的影响,设置了三个情景并对设备最优出力和热网最优运行状态进行对比分析。

1 热网建模

供热系统常用蒸汽和热水作为载热介质,中国采暖、通风和热水负荷均以热水作为载热介质[18]。本文所建立的热网模型基于热水供热系统,采暖热用户与热水网路采用无混合装置的直接连接方式,通风用热设备与热水网路采用最简单的连接方式[18],热水供应热用户通过表面式水—水换热器与热水网路相连,采用无储水箱的连接方式。供热采用质调节并且满足水力工况要求。

将热网看作流体网络,如图1所示,每根管段为一条支路,热源、热用户和管道的连接点为节点。热网模型共包含节点流量平衡、节点功率融合、负荷取用特性、供回水温度约束和管段传热特性5个部分。图中：bi表示管道；Li表示负荷；Si表示热源。

图1 热网示意图Fig.1 Schematic diagram of heating network

1.1 节点流量平衡

对于热网中任一节点,流入的热媒流量之和等于流出的热媒流量之和,即

(1)

(2)

1.2 节点功率融合

由能量守恒定律可知,对于热网中的任一节点,流入的功率之和等于流出的功率之和,即

(3)

(4)

式中:TSF和TEF分别为由管段始、末温度和流量组成的列向量;Tsi和Tei分别为第i根管道的起始温度和末端温度,其中i=1,2,…,b。

节点处发生功率融合后,该节点的温度与流出该节点的热媒温度相等,即

Tni=Ts1,i=Ts2,i=…=Tsk,i

(5)

式中:Tni为第i个节点的温度;Ts1,i,Ts2,i,…,Tsk,i为所有与第i个节点直接相连,并且热媒流出该节点的管段的起始温度。

1.3 负荷取用特性

如图2所示,对于包含热用户的热网支路,供、回水管段的温度与热用户的取用功率满足式(6)。

(6)

(7)

式中:TLI和TLO分别为所有热用户处的供水温度和回水温度构成的列向量;c为热媒比热容,取值为4.2 kJ/(kg·℃);ρ为热媒密度,取值为934.667 kg/m3;ηHX为热网负荷端各换热设备的平均效率;QL/F为所有热用户的取用功率与管道流量组成的列向量;QLi和fLi分别为第i个负荷取用的功率和其所在管段的运行流量,其中i=1,2,…,k。

图2 含有热用户的热网管道示意图Fig.2 Schematic diagram of pipeline in a heating network with heat users

1.4 供回水温度约束

为了保证热源和热用户的供热质量,需要对热源和热用户的供、回水温度进行限制,即

(8)

式中:TSO和TSI分别为热源的供、回水温度;TLI和TLO分别为热用户处的供、回水温度;下标min和max分别为对应参数的最小值和最大值。

1.5 管段传热特性

热网依赖热媒的流动实现能量传输,热媒输送的迟滞可能会导致数分钟到数小时不等的功率传输延迟,这对于综合能源系统的超短期调度可能产生显著影响。

1.5.1稳态传热特性

管段的稳态传热特性是指管段内热媒的温度随传输距离的变化关系,当管段的传输时延远小于系统调度策略的时间尺度时,可以使用稳态传热公式近似地描述热网的传热特性[7, 19],如式(9)所示。

(9)

式中:x为管段上某一点与管段首端的距离;R为管段单位长度的热阻;Ts,Te,Ta分别为一根管段的首端温度、x处温度和外界温度;f为热水流量。

考虑到式(9)指数项中x的系数接近于零,可以将其泰勒展开并略去高次项,得到线性化后的形式为:

(10)

将式(10)改写成矩阵形式:

TE′=ηTS′

(11)

(12)

式中:TS′和TE′分别为由管段首端温度、x处温度和外界温度构成的等效管段起始温度列向量和等效管段末端温度列向量;η为由管段参数构成的矩阵。

1.5.2暂态传热特性

管段的暂态传热特性是指管段上某一点的温度从一个稳态变化到另一个稳态的过渡过程,当管段的传输时延与系统调度策略的时间尺度相当时,应当使用暂态传热公式描述热网的传热特性,以保证调度策略的精确性。

如图2所示,取管段内长度为dl的流体微元进行分析,设其从热源发出时的初始温度为Ts。不计流体微元之间的相互作用,仅考虑流体微元通过管壁对外界散失热量Hloss,由傅里叶定律可知:

(13)

式中:λ为管段的热导率;A为流体微元等温表面的传热面积;δ为管壁厚度；T为温度。

初始时刻,该流体微元刚从热源处发出,具有的能量Hs为:

(14)

式中:d为管段的内径;Tr为管段的回水温度。

t时刻该流体微元具有的能量等于初始能量减去散失的热量,即

(15)

式中:T(t)为该流体微元在t时刻的温度。

联立式(13)至式(15)可以解得管段内该流体微元的温度随时间的变化关系,如式(16)所示。

(16)

若该流体微元经过时间t后到达管段x处,则

(17)

将式(17)代入式(16)可得此时流体微元的温度为:

(18)

此温度即为管段x处的稳态温度(见式(9)),即经过时间t后,管道x处的温度恰好达到稳态。

由于传导、对流以及流体之间复杂的水力作用,加之摩擦热等因素的影响,管段某一点处温度由初态变化到稳态的暂态过程难以精确建模[14]。为了工程应用的方便,本文采用线性模型描述暂态传热过程,即假设管段x处从初态温度到稳态温度的过程随时间线性变化,则一维管段的暂态传热特性可表示为:

T(x,t)=

(19)

(20)

式中:T(x,t)为距离热源x处的热网管道在t时刻的温度;Ts和Ts′分别为初态时和稳态时的热源温度;α和β为常数。

将式(19)推广至热源处进行多次质调节的情况。

1)对于距离热源较近的地方,暂态过程较短,在一次调节之后、下一次调节之前,管段温度已经达到稳态,这些点处管段的暂态传热特性可以表示为:

Ti(x,t)=

(21)

2)对于距离热源较远的地方,暂态过程较长,在一次调节后,温度尚未达到稳态,下一次调节已经开始,这些点处管段的暂态传热特性可以表示为:

(t-ti-1)+Ti-1(x,ti-1)t∈[ti-1,ti]

(22)

式中:Ti-1(x,ti-1)为第i-1时段内,距离热源x处的热网管道在ti-1时刻的温度；i=1,2,3,…。

1.6 模型评估

由式(17)可知,从一根管段首端流入的热媒微元经一个调度周期Δt后,若未到达该管段的末端,则该管段存在暂态传热特性,即

(23)

式中:L为管段长度。

式(23)即为热网是否存在暂态传热特性的判据。记临界时长tc表示热媒微元从管段首端运动到管段末端所需要的时间,则

(24)

下面依据文献[20]提供的实测数据对本文所提出的线性传热模型的误差及其适用范围做定性分析。

图3展示了热网中某一管段的首端温度变化时,其末端温度变化情况的实测值、稳态传热模型值和线性传热模型值。以管段首端升高温度为例,当调度周期小于临界时长的2/3左右时,相较于普遍采用的稳态传热模型,本文提出的线性传热模型与实测情况更加接近,并且调度周期越短,线性传热模型在减小误差方面的优越性较稳态传热模型体现得越明显。因此,线性传热模型适用于系统调度周期小于管段临界时长2/3的情况,超出这一范围时,宜使用稳态传热模型。

2 能量优化管理模型

在多时间尺度能量优化管理模型中,超短期调度以5～15 min为周期不断修正可再生能源和负荷功率的预测值,在日前计划的基础上加入滚动优化环节以减小与实际情况的偏差[21]。为了体现热网的暂态传热过程,取15 min为滚动优化的周期。

图3 热网管段首、末端温度的实测值与模型值对比图Fig.3 Contrast of initial and terminal temperatures between measured values and model values

2.1 目标函数

对于并网运行的综合能源系统,滚动优化的目标函数是使未来4 h内的运行费用最小[22-23],即

minC=Ce+Cg

(25)

(26)

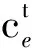
2.2 约束条件

2.2.1功率平衡约束

系统源设备发出的各种功率经转换设备和传输网络输送至负荷端时,应满足负荷端的功率需求,能量的转换和传输过程满足能量守恒定律。以本文的综合能源系统算例为例(相关参数见附录A),热源S1由燃气轮机和余热锅炉共同组成,热源S2为燃气锅炉;负荷QL1,QL2,QL3分别为商业区、办公区和住宅区热负荷,热源端热功率的平衡约束可由式(27)表示,冷、电功率平衡约束不再赘述。

(27)

QSi=cρfSi(TSO,i-TSI,i)

(28)

2.2.2热网特性约束

供热系统采用质调节方式,运行流量固定,节点流量平衡方程自动满足,除此以外,节点功率融合、负荷取用特性、供回水温度约束以及管段温降特性应当分别满足。由于热网负荷端存在热水型吸收式制冷机组,负荷取用特性约束由式(29)表示。

(29)

式中:QL/F,i为QL/F的第i个元素；ηABC为吸收式制冷机的制冷系数;CABC为吸收式制冷机输出的制冷功率。

此外,热网中的每个热源都是由实际的设备组成,因而每个热源的供热功率应该与相应设备的输出功率相等。以本文的综合能源系统为例,每个热源的约束可由式(30)描述。

(30)

2.2.3其他约束

系统各设备应该满足各自的输出容量约束和爬坡约束。对于储能设备,还应该满足蓄/放能功率约束和状态变量约束[5]。

3 算例分析

3.1 参数设置

本文所构建的综合能源系统相关参数见附录A,系统结构图见图A1(a),各设备参数见表A1。热网结构图见图A1(b),热网参数见表A2。系统冷、热、电负荷和光伏出力均使用滚动预测值,视为已知量,数值见图A1(c)。分时电价和天然气价格见图A1(d),算例系统初态见表A3。

3.2 结果分析

为了便于比较分析,将考虑热网暂态传热特性的情况作为情景1,仅考虑热网稳态传热特性而不考虑暂态特性的情况作为情景2,不考虑热网传热特性的情况作为情景3。程序在Win10操作系统下配置有Intel(R) Xeon(R) CPU E3-1230 V2 @ 3.30 GHz处理器和8 GB内存的计算机上运行。

3.2.1情景1运行优化结果

图4(a)至(c)展示了考虑热网暂态传热特性时算例系统的优化运行结果。图中1个时段为15 min,下同。在电价较低的时段(00:00—07:00),系统所需电负荷主要由电网购电满足,随着电价的上升,燃气轮机逐渐成为供电主体。在热网热源端,从07:00开始,燃气锅炉出力随着燃气轮机出力的增加而有所减少。制冷功率方面,吸收式制冷机仅在15:45—17:00和19:15—24:00有明显出力,其余时段均由电制冷机提供制冷功率。

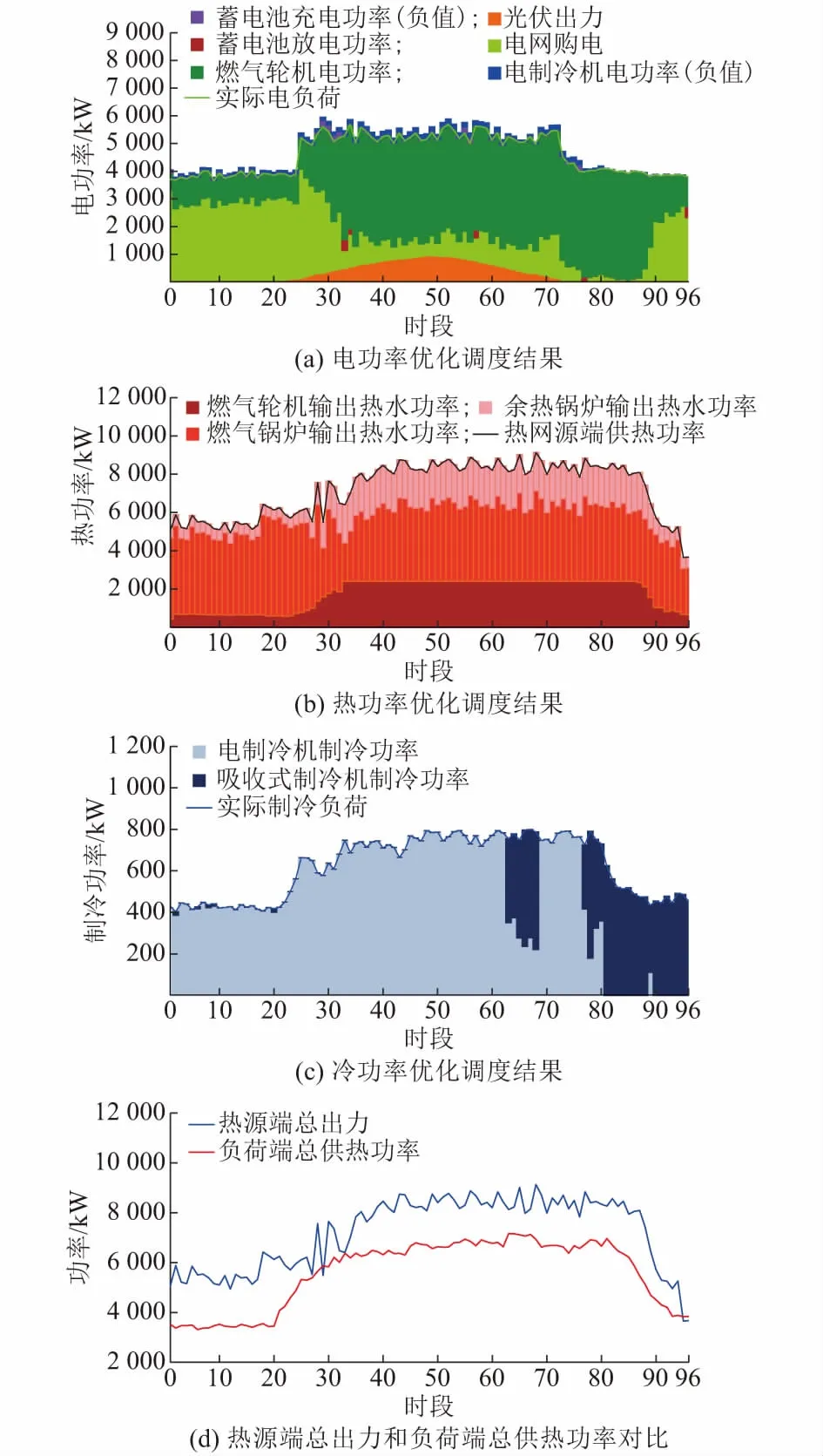
图4 情景1功率平衡关系Fig.4 Power balance relationship in situation 1

图4(d)展示了系统热源端总出力和负荷端总需求的实时匹配关系。热网自身的传热特性改变了系统热功率的供求匹配机理,复杂的拓扑结构和传输时延造成的蓄热特性,以及沿程的功率衰减,使得热源端和负荷端的供、求热功率不必实时匹配。对于整个系统而言,热网运行时就像一个储能设备,按经济性最优的原则进行蓄、放能。情景1和情景2由于考虑了热网的传输特性,系统热源端总出力和负荷端总需求均不再实时匹配,而情景3忽略了热网的传输特性,系统供求热功率实时匹配。

3.2.2不同情景的优化运行结果对比

1)日运行成本和模型求解时间对比

三种情景下系统日运行成本和优化模型的求解时间对比情况如表1所示。情景2忽略了热网的暂态传热特性,认为管段温度瞬间达到稳态值,这放大了有暂态传热过程的管段损耗,使得情景2的热网损耗略大于情景1,日运行成本略高于情景1。情景3未考虑热网传热特性,因而没有热网损耗,日运行成本也最低。依据热网模型的复杂度,情景1至情景3的求解时间依次递减。

表1 三种情景下系统日运行成本和模型求解时间对比Table 1 Contrasts of daily operating costs and model solution time of system in three situations

2)燃气锅炉运行状态对比

三种情景下燃气锅炉功率出力的对比情况如图5所示。情景1和情景2中的燃气锅炉功率出力有较明显差异。情景3中燃气锅炉的输出功率与情景1和2中的情况差异显著,由此可见热网特性对于综合能源系统的优化运行影响显著。

图5 三种情景下燃气锅炉输出功率对比Fig.5 Power output comparison of gas boiler among three situations

3)热网运行状态对比

图6展示了情景1和2中热源S2和负荷QL2处的供水温度对比情况。可以看出,在考虑热网暂态传热特性前后,热源和负荷的供水温度均有明显变化,可见在系统超短期调度中应考虑热网暂态传热特性。

4 结语

本文建立了综合考虑回水管网拓扑结构、热网暂态传热特性和传输时延的热网模型,着重研究了管段的暂态传热特性,推导出依据调度周期和管段长度判断管段暂/稳传热特性的公式。此外,本文所建立的热网模型适用于不同拓扑结构的二维、三维热网,并且可以方便地推广到量调节、分阶段改变流量的质调节、间歇调节等情况。

图6 情景1和情景2中热网优化运行状态对比Fig.6 Comparison of optimal operation states of heating network in situation 1 and situation 2

为了反映热网特性对于超短期调度的影响,本文设置了三个情景并进行对比分析。算例结果表明,热网传热特性改变了系统热功率的供求匹配机理,复杂的拓扑结构和传输时延造成的蓄热特性使得热源端和负荷端的供、求热功率不必实时匹配。考虑热网暂态传热特性前后,供热设备的最优出力变化显著,系统日运行成本稍有降低,热源和热负荷的供水温度均有明显变化,由此可见考虑热网暂态传热特性在系统超短期调度中的必要性。

但是,本文所采用的热网暂态传热特性模型也有一定的局限性,模型误差会随着调度周期的改变而改变,并可能达到相当可观的量级。此外,本文的换热器模型未能反映供回水温度与换热功率的单值对应关系,有待进一步完善。建立更加精确的热网传热特性模型和换热器模型将是今后的研究重点。

针对审稿意见的答复与讨论见附录B,期待更多的学术探讨。

本文受到国网浙江省电力公司科技项目(5211DS16002H)资助,特此感谢!

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。