裂隙水流运动的入渗试验及数值模拟研究
2018-07-26程勤波张志才张润润黄日超蔡炼彬河海大学水文水资源学院江苏南京210098河海大学水文水资源与水利工程科学国家重点实验室江苏南京210098
程勤波,陈 喜,张志才,张润润,丘 宁,黄日超,蔡炼彬(1.河海大学水文水资源学院, 江苏 南京 210098;2.河海大学水文水资源与水利工程科学国家重点实验室, 江苏 南京 210098)
由于构造、风化、卸荷等作用,岩体裂隙在自然界中广泛存在。由于岩体裂隙的渗透性远大于基质岩体,裂隙是岩体的主要导水介质。在可溶性石灰岩地区,裂隙控制水流运动,因此,研究岩体裂隙中流体运动规律对于了解喀斯特流域水动力过程以及溶质运移具有重要意义[1]。
Poiseuille在均质恒定运动条件下,导出了单片光滑平行板裂隙中水流运动的理论公式,即立方定律[2]。Lomize[3]和Louis[4]各自采用平行玻璃板模拟裂隙壁,证明了在层流时立方定律的有效性。然而,天然裂隙面多粗糙不光滑,并且裂隙宽度多存在小范围的不平整和大范围的起伏,不符合立方定律假设条件。Djik和Berkowitz运用核磁共振技术研究饱和粗糙裂隙中水流场分布,结果显示裂隙横断面水流速度呈类似抛物线,但不完全对称[5]。鉴于立方定律的局限性,众多学者基于室内外实验和数值模拟结果提出了各种形式的修正公式,其核心思想是修正裂隙宽度[2~6]。
隙宽等裂隙特征是控制裂隙导水能力及水流运动的主要因素,目前主要根据自然界岩体出露面测量裂隙隙宽,但由于自然岩体裂隙中存在大量粗糙面,当前技术还无法对自然界裂隙壁的粗糙程度及有效隙宽精确测算。对于非充填裂隙,Navier-Stokes(N-S)方程组描述裂隙水流运动比连续性方程具有更高的精度,但数值求解N-S方程组非常困难,因而将N-S方法应用于野外原位实验研究裂隙水流运动规律鲜有报道[6]。目前大多数软件基于立方定律的连续性方程数值解模拟裂隙水流运动,主流裂隙水模拟软件有:TOUGH,RockFlow,FracMan/MAFIC等[7]。
为研究自然岩体裂隙对入渗水流运动作用,本文选取具有垂向与横向裂隙交错的典型岩体,利用现场单环注水入渗试验,分别基于N-S方程组、立方定律的连续性方程建立裂隙入渗水流运动数值模型,以实测单环水位变化为目标,采用试算法,推求裂隙水力隙宽及入渗水流在不同裂隙中的比例。对比两种模型计算结果,分析裂隙水数值模拟中立方定律适用性。
1 野外裂隙入渗实验
试验地位于贵州省普定县陈旗村董家山阴坡岩石开挖剖面,该处岩石属于三叠系关岭组灰岩。试验岩块有两条较为发育的纵向裂隙面(图1中①、③号),其中,①号裂隙面实测隙宽为1 mm,沿岩石面垂向(图2中Z方向)裂隙长56 cm,垂直于岩石面(Y方向)裂隙长约60 cm;③号裂隙面实测隙宽为2 mm,沿Z方向、Y方向裂隙面裂隙长度都约为60 cm。在横向(X方向),有条较发育的岩层解理面(②号裂隙),裂隙面隙宽为1 mm,倾向164°,倾角8°,沿X、Y方向裂隙面裂隙长度分别为60 cm和47 cm(图1)。

图1 岩体剖面照片及主要裂隙Fig.1 Photo of the rock profile and fractures
裂隙面均无明显填充物,实测裂隙宽是裂隙出露面处的平均隙宽。为便于数值模型中网格划分及提高数值解的收敛性,裂隙面均概化为平面,即裂隙宽度沿程不变。
为研究各裂隙对入渗水流影响程度,按上述三条裂隙组合分为三种模式(图2):(a)单条垂向裂隙(①号裂隙);(b)横向与垂向裂隙组合(①②号裂隙);(c)一条横向与两条垂向裂隙组合(①②③号裂隙)。
单环裂隙入渗试验步骤:(1)将单环罩于上表面裂隙上、水位计置于单环内(图1,单环半径为15 cm);(2)瞬时将单环水位加注到H0(=0.0743 m);(3)自记水位计自动记录单环水位下降过程。

图2 3种岩石裂隙概化模式Fig.2 Three cases of the conceptual rock fractures
根据雷诺数(Re)判别裂隙水流的流态,用以选择合适的数学模型[2]。根据实测单环水位下降最大速度得裂隙水流最大雷诺数为68,远小于临界值1 150[2],所以本次试验裂隙水流流态为层流。
2 数值模拟方法
2.1 Navier-Stokes方程组
非饱和无填充裂隙水流入渗问题可视为水流驱替空气问题,该问题属于流体力学中的水和空气的两相流问题。描述水、空气运动的Navier-Stokes方程组[8]为(简称N-S方程):
连续性方程:

(1)
动量守恒方程:
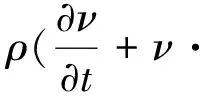
(2)
式中:ρ——流体密度/(kg·m-3);
ν——流体速度/(m·s-1);
t——时间/s;
W——源汇项/(kg·(m3·s)-1);
p——静压/Pa;
G——重力体积力/N;
f——其它体积力(如两相流体间的作用)/N;
Γ——应力张量/N。
对于可压缩流体,应力张量计算公式为:
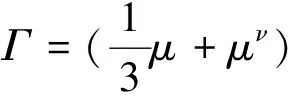
对于不可压缩流,应力张量计算公式为:
Γ=μ(·ν)
式中:μ——动力黏度/(kg·(m·s)-1);
μν——第二动力黏度/(kg·(m·s)-1);
对可压流体(空气),采用理想气体方程描述密度与压强的关系[8]:
(3)
式中:R——普适气体常数/(m2·(T·s2)-1);
T——绝对温度/K。
对于水、空气两相流问题可采用容积比率模型(简称VOF)模拟:VOF模型假设水与空气不相容,并且两流体不会互相穿插,在整个流场内采用统一N-S方程组求解,但在不同相中方程组参数不同(如流体密度、动力粘度、压缩公式)。在流体交界面处,计算单元格各相的容积比率(容积比率之和为1),根据容积比率计算方程组在该单元格内参数的平均值[8],单元格平均密度ρ可采用如下公式计算:
ρ=α1ρ1+α2ρ2
(4)
式中:α1,α2——水和空气所占容积比;
ρ1,ρ2——水和空气密度/(kg·m-3)。
2.2 单环水位变化模拟
相对于裂隙,由于单环容积大,水位变化缓,单环内水动力现象不突出,单环水位变化控制方程采用如下水量平衡方程:
(5)
式中:H——单环水位/m;
Q——裂隙入流率/(m·s-1);
νf——裂隙入渗面的流速/(m·s-1);
S——裂隙入渗面的面积/m2。
单环水位对时间的离散形式可写为:
(6)
式中:Qtn——t时刻,n次迭代期裂隙面入流率/(m·s-1);
Qt-Δt——t-Δt时刻裂隙面入流率/(m·s-1)。
2.3 基于立方定律的连续性方程
对于具有充填物的裂隙或裂隙隙宽小的非填充裂隙,水流速度一般较小,多属符合达西水流规律的层流,可采用基于达西定律和立方定律的连续性方程研究裂隙水流运动[7,9],其非饱和流微分方程形式为:
(·
(7)
式中:h——水势/m;
K——渗透系数/(m·s-1);
C——立方定律修正系数;
d——裂隙隙宽/m;
Θ——饱和度;
Ss——贮水率/m-1;
c——比水容量/m-1。
3 数值模拟及结果分析
3.1 基于N-S方程组的数值模型构建及模拟结果
3.1.1数值模型构建
本文采用基于有限体积法求解N-S方程组的FLUENT软件建模求解[8]。针对裂隙入渗实验,使用FLUENT软件建模,其中,裂隙中水流驱替空气过程模拟选用FLUENT中的两相流模型(VOF模型);针对入渗单环水位变化的模拟,由于FLUENT提供的现有边界模式中,没有变水头入渗边界模式,本文采用FLUENT提供的用户接口(UFD),遵照C语言书写规范,编制了模拟单环水位变化的UFD代码模块,作为裂隙水流运动边界条件。
裂隙水流数值模型构建中非常重要、也较为困难的是网格剖分。本文先采用Gambit软件[8]将裂隙面剖分成1 cm×1 cm的四边形网格,再沿裂隙壁将裂隙剖分成6层,构建出裂隙空间的三维网格系统。
初始状态设置为空气,初始含水量设置为零,无残余含水量。N-S模型参数(如动力粘度(μ),流体密度(ρ)和重力加速度(g))均采用FLUENT软件默认值,这些值均源于大量实验测定结果[8]。
3.1.2裂隙水力宽度推求
由于天然裂隙壁粗糙不光滑,裂隙宽度沿程变化,因此实测裂隙宽度与裂隙的水力宽度一般不一致,研究表明水力宽度远小于实际宽度[6]。本文以数值模型计算的单环水位与实测水位之差最小为目标,采用试错法推求实际剖面中三条裂隙组合情形下(图2c)各裂隙水力宽度。由于每次调整裂隙宽度都需要重新做网格剖分,比较繁琐,因此为减少计算量,三条裂隙水力宽度按裂隙实测宽度同比调整。推求的①②③号裂隙水力宽度分别为:0.25 mm、0.25 mm、0.50 mm。数值模型计算的单环水头与实测水头变化过程见图3,两者较为接近。图3中模拟前期,模拟值明显偏小于实际值,这主要是由于在水流浸润过程中裂隙的水动力宽度比水流稳定之后的水动力宽度大,而试错法拟合得到的隙宽仅为该裂隙在时间、空间上的综合(平均)水动力宽度。
3.1.3不同裂隙组合情形下入渗水流模拟
三种裂隙组合情形下(图2)分别模拟的单环水位变化过程见图3。可以看出,水头模拟误差随着岩体裂隙概化合理性增大而减小,仅一条垂向裂隙和两条裂隙组合情形比三条裂隙情形所模拟的单环水位高。在①、②两条裂隙间设定监测断面I、在②、③两条裂隙间设定监测断面II(图2),计算通过断面I、II水流速度过程见图4,入渗结束时裂隙中压强、含水量、水流速度分布见图5。
根据图4中设定的监测断面水流速度模拟结果,得到通过断面I、II的入渗水量:两条裂隙情形下(图2b),83.3%入渗水沿垂向裂隙(①号)下渗,剩余16.7%通过水平向断面I入渗;三条裂隙模拟情形下(图2c),沿垂向裂隙(①号)入渗水流占75.9%,通过断面I的水平流量占总入渗量的24.1%,该部分水流中,通过断面II的流量占总入渗量的21.8%。因此,三条裂隙情形下通过水平向I断面的入渗水量比两条裂隙情形大7.4%,说明入渗水运动不仅取决于垂向、水平向裂隙发育程度,而且取决于裂隙连通程度。但总体而言,与单环入渗面直接连接的垂向裂隙入渗水量占主要部分。

图3 三种裂隙情形中模拟的单环水位变化与实测值对比图Fig.3 Comparison of the measured and simulated water levels for three rock fracture cases

图4 FLUENT中两监测断面流速变化图Fig.4 Simulated flow velocity of two monitoring sections with the FLUENT model
图5压强分布表明,FLUENT软件计算出的压强具有较好的连续性;含水量分布中三种情形求得的裂隙①的含水量分布差异较大,表明FLUENT中两相流模型(VOF模型)在复杂水流情况下会出现异常结果,但这并没有影响压强及速度计算结果;流速分布表明,渗出面附近流速较大,水流多从溢流面底部渗出。

图5 FLUENT软件模拟末期裂隙中压强、含水量、水流速度分布图Fig.5 Pressure, water content and velocity distribution at the end of simulation with FLUENT
3.2 基于立方定律的数值模型构建及模拟结果
3.2.1数值模型构建
非填充裂隙中水分入渗过程需要考虑水气两相流运动,难度较大,而且岩体裂隙宽度较小,裂隙容水量少,水分会瞬时充满裂隙,运用立方定律可忽略裂隙水的浸润过程,仅考虑饱和裂隙水流问题。SUTRA是美国地质调查局(USGS)开发的饱和、非饱和带水流计算程序,广泛应用于土壤水及地下水数值模拟[19]。
利用SUTRA模拟裂隙入渗水流实验时,有两类边界需要特殊处理:(1)单环入渗边界。根据单环水位变化公式编写单环水位模拟程序,将计算的单环内水压设置为SUTRA中的变水头边界。(2)裂隙溢流边界。可采用溢流面设置方法,将溢流面处计算节点设置为SUTRA中的变水头边界,根据临近节点压强计算该处节点压强,当临近结点压强大于0(饱和)时,则该节点压强设置为0,反之,该节点压强设置与临近节点压强相等。该方法可有效防止回流,确保渗流面出流通畅。考虑到裂隙的储水能力小,裂隙含水量对裂隙水量影响较小,因此将裂隙初始压强值设置为0,确保裂隙渗流面出流通畅。
为仿真模拟裂隙水流运动,在SUTRA中将所有计算节点区分为:饱和节点和非饱和节点。饱和节点含水量为1,渗透系数为饱和渗透率,而非饱和节点含水量接近0,渗透系数也应该近似为0。SUTRA采用VGM模型描述非饱和水动力特征:
(8)
式中:θ——土壤饱和含水量;
θr——土壤残余含水量;
K——土壤非饱和渗透系数/(m·s-1);
Ks——土壤饱和渗透系数/(m·s-1);
α,n,m——VGM模型经验参数,其中m=1-1/n。
当α→∞时,K→0,同时θ→θr。这说明当α取较大值时,SUTRA可模拟出裂隙中的非饱和节点特征。考虑到算法的稳定性,经过多次测试,本研究采用如下非饱和水动力参数值:α=0.002/Pa,n=2,θ=1,θr=0。依据FLUENT求得的最佳水力裂隙宽度,及立方定律可求得①②③三条裂隙的饱和渗透系数分别为:0.051, 0.051和0.204 m/s。由于N-S方程在模拟裂隙水流运动中存在误差(图3),因此N-S方法推求的裂隙宽度可能与实际情况存在差异,从而导致SUTRA模型中裂隙饱和渗透系数估计不准。所以此处将集中讨论SUTRA与FLUENT模拟结果的差异,并据此探讨裂隙水数值模拟中立方定律的适用性,而忽略SUTRA模型模拟单环水头的准确度。
数值模型SUTRA网格划分同样采用Gambit网格剖分软件:先将裂隙面剖分成1 cm×1 cm网格,再沿裂隙壁将裂隙剖分3层。网格划分好后,可输出网格节点编号及坐标,再组织成SUTRA所需的格式即完成数值计算所需的网格剖分。
3.2.2不同裂隙组合情形下入渗水流模拟
根据裂隙入渗实验的概化结果,利用SUTRA建立三种裂隙组合情形的数值模型,模拟的单环水位变化见图6,通过监测断面I、II的流速见图7,入渗结束时裂隙中压强、含水量、水流速度分布见图8。
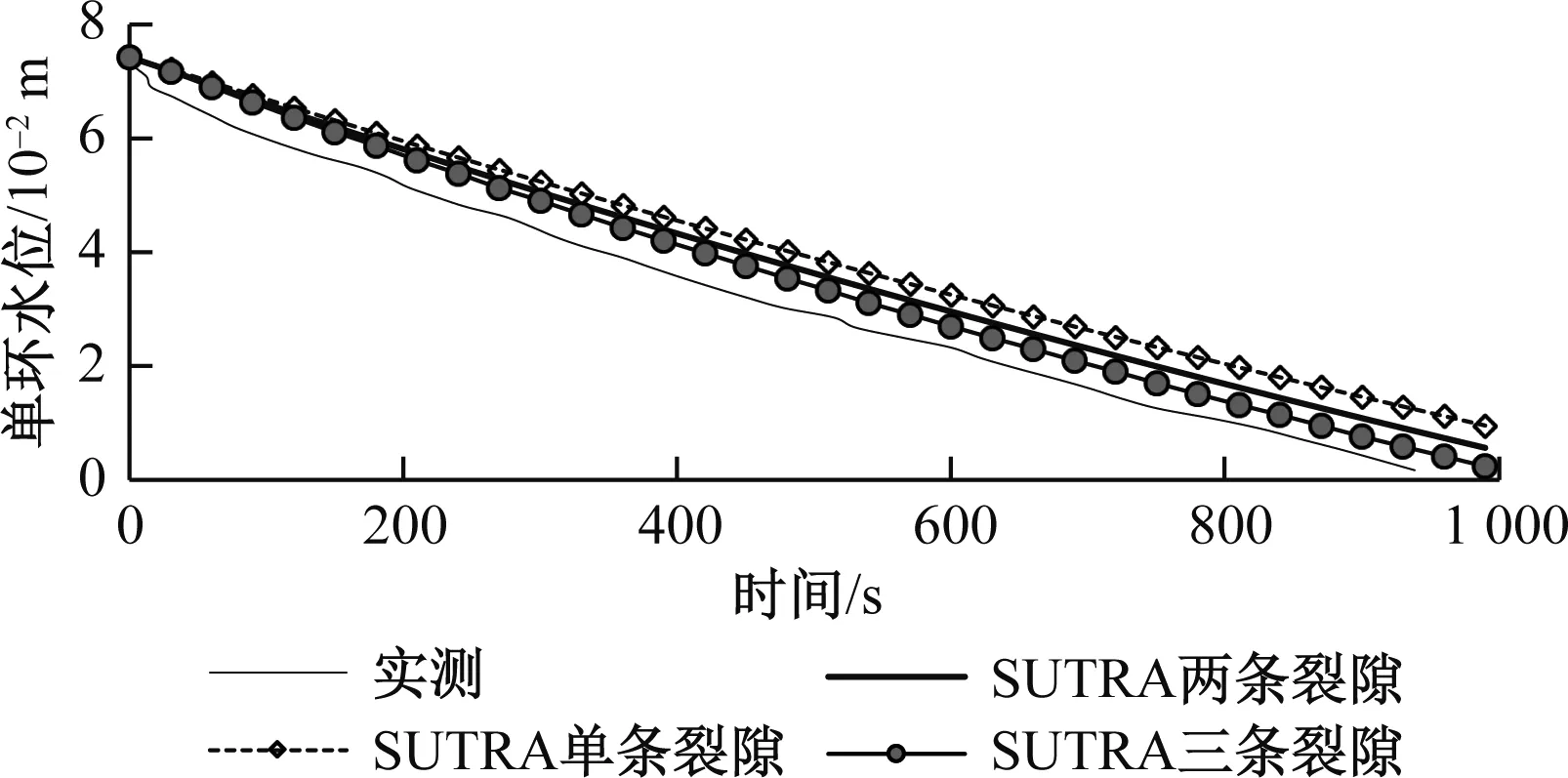
图6 三种裂隙分布情形中单环水位模拟与实测值对比图Fig.6 Comparison of the measured and simulated water levels for three rock fracture cases
图6显示随着裂隙条数的增加,SUTRA模拟的单环水位下降速度增大。图7中,两条裂隙模拟情形下通过I的流量占总入渗量的19.5%,三条裂隙模拟情形下通过I的流量占总入渗量的33.8%,通过II的流量占总入渗量的31.0%;与FLUENT相比,沿水平侧渗量要偏大,但总体而言,沿主渗流面(①号裂隙面)入渗量占主导,三条裂隙情形下,所占比例为66.2%。
图8表明,SUTRA计算出的压强和含水量分布具有较好的连续性,尤其是含水量分布并未出现不合理现象,表明SUTRA模型具有较好的稳定性;流速分布显示渗出面底部水流速度较大,表明水流多从溢流面底部渗出。
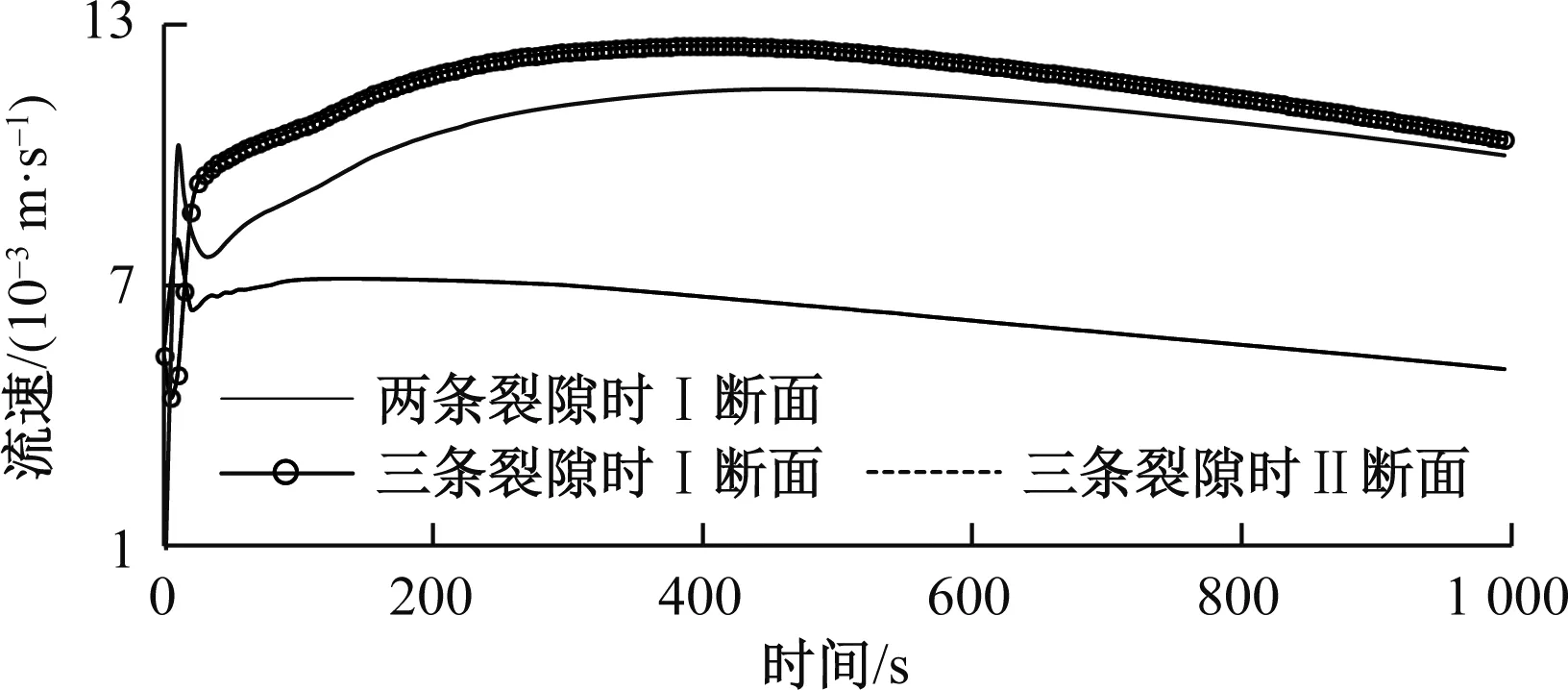
图7 SUTRA模拟的断面流量变化图Fig.7 Simulated flow velocity of two sections with SUTRA

图8 SUTRA模拟末期裂隙中压强、含水量和水流速度分布图Fig.8 Pressure, water content and velocity distribution at the end of simulation with SUTRA
3.3 两种模拟方法比较
理论上,N-S方程可以推导出达西定律与立方定律[3],换而言之,基于立方定理的连续方程水流模型仅为N-S方程在裂隙介质中的简化形式。然而N-S方程求解过于复杂,因此在实际应用中常采用基于立方定理的连续性方程模型。
两模型单环水位模拟结果(图3、图6)对比表明:SUTRA模拟的单环水位下降速率小于FLUENT计算结果。原因可能是SUTRA模型(基于立方定律)计算的是裂隙断面平均流速,而N-S模型能刻画裂隙横断面水流流速的抛物线分布(即“优势流”),其实际流速要快于SUTRA计算的平均流速。同时,FLUENT模拟的单环水位下降速率的变化率(图6)也大于SUTRA(图3),这反映出FLUENT模型对水位变化的敏感性比SUTRA模型大,因为其在裂隙断面上流速的差异随着单环水位(压强)减小而减小。
两模型模拟的监测断面出流过程差异较大(图4、图7),总体说来FLUENT模拟的水流过程更加细致,因为其模拟了水、气驱替过程,而SUTRA模拟结果则相对平顺。
SUTRA模拟的裂隙压强和流速分布(图8)与FLUENT模拟结果(图5)近似,但含水量分布与FLUENT有明显差异,这反映出SUTRA中用于概化两相流运动的方法存在误差,主要表现为非饱和节点含水量消退较慢。同时,SUTRA模拟的流速分布(尤其在渗流面附近)比FLUENT模拟结果平缓,其主要原因可能是SUTRA模拟的单元格出流能力(即平均流速)小于FLUENT模拟结果(即可描述“优势流”的抛物线型流速)。该因素同时也导致SUTRA模拟的溢流高度大于FLUENT结果。总体而言,基于Darcy定律和立方定律的连续性方程模型可用于近似模拟裂隙水流运动。
4 结论
(1)以实测单环水位变化为目标,FLUENT推求的裂隙等效水力宽度仅为实测裂隙宽度的1/4,远小于实测隙宽,这与以往研究成果相符。
(2)FLUENT计算结果表明,岩体裂隙概化越符合实际情况,其单环水头模拟误差越小;裂隙水流大部分沿垂向裂隙下渗,但也有部分(约20%)水流沿横向裂隙侧向运动。
(3)SUTRA模拟结果表明,随着裂隙条数的增加,SUTRA模拟的单环水位下降速度增大,但单环水位下降速率的变化率小于FLUENT计算结果,这是由于N-S方程能刻画裂隙横断面水流速度的抛物线分布(即“优势流”),而立方定律则只能反映裂隙断面的平均流速;SUTRA模拟的压强、流速分布与FLUENT模拟结果接近,因此基于达西定律和立方定律的连续性方程模型可用于近似模拟裂隙水流过程。
(4)在实际应用中,由于N-S方程求解复杂繁琐,不便于区域数值模拟计算,因此采用连续性方程求解裂隙水流问题更为方便有效。
