定时同步与匹配滤波频域联合实现技术

2018-07-26吴艺彬邵高平

信号处理 2018年9期

吴艺彬邵高平汪洋

(中国人民解放军战略支援部队信息工程大学，河南郑州 450001)

1 引言

随着卫星技术和星上有效载荷技术的发展，卫星所需传输的数据量急剧增加，使得地面接收系统向高速宽带数字处理发展。但是受常用数字处理器(如FPGA)稳定工作时钟频率的限制[1]，传统的串行处理技术显然无法满足高达Gsps采样率数据流的实时处理，因此要想突破处理器时钟频率的限制，提高系统通信速率，就必须采用并行处理技术。

一般来说，常用的并行解调架构可分为时域并行结构、频域并行结构。由于频域并行结构，具有运算量低、实现简单的特点，更适用于高速通信，因此高速环境下一般选用该结构[2]。但是伴随系统调制符号速率的提升和并行路数的增加，传统的频域并行架构已经无法满足实时通信的需求，需要对系统算法和系统架构做改进。文献[3]参照Gardner算法提出了一种改进的插值结构，不仅提高了精度，还降低了实现难度。目前算法改进研究较多且较为成熟，优化空间较有限。文献[4- 6]从系统架构入手，通过采用免混频、并行滤波器的简化等方式，有效降低了系统的实现复杂度和硬件资源使用。该种方法的优点在于通过使用快捷算法，在不改变系统性能的前提下简化系统实现，但是未能考虑到模块间的算法特点，充分复用模块间的公共资源。因此文章围绕系统模块间资源的复用问题，对该架构进行了进一步改进，改进后的并行架构计算量更低、适用性更强。

2 基于免混频的频域并行解调架构

为避免NCO(数字控制振荡器)模块的不稳定性，降低架构实现的复杂度，文献[4]将免混频结构引入到传统的并行解调架构中去，并对匹配滤波器模块进行了改进。改进后的架构可表示为如图1所示。

2.1 免混频结构的定义

设I(t)、Q(t)分别是发送信号符号的I、Q分量，fc表示载波频率，fs表示采样率，则接收到的中频信号为：

s(t)=I(t)cos(2πfct)-Q(t)sin(2πfct)

(1)

取4fc=fs，采样后信号表示为：

s(n)=I(n)cos(2πfcn/fs)-Q(n)sin(2πfcn/fs)=

-I(2),Q(3),I(4),-Q(5),...]

(2)

由式(2)可以看出，只需要对采样后中频信号进行分路、插零、取反，便可以得到I、Q两路的基带信号：I(n)=[I(0),0,I(2),0,…]，Q(n)=[0,Q(1),0,Q(3),…]。而后将两路基带信号分别通过低通滤波器便可以得I、Q两路的基带信号。将这种不需要进行数字下变频的特殊结构称为免混频结构[5]。

2.2 匹配滤波器的简化结构

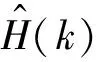
(3)

(4)

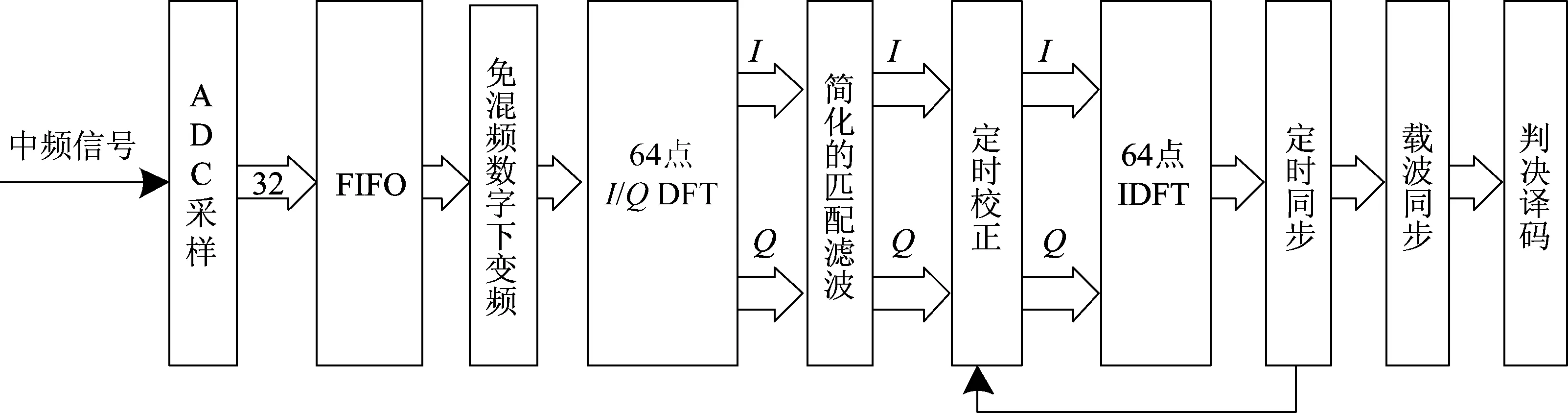
图1 并行解调架构系统流程图Fig.1 The flow chart of parallel demodulation architecture system

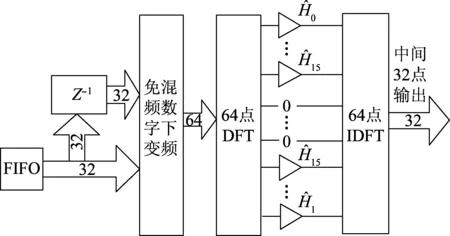
图2 频域匹配滤波简化实现结构Fig.2 The simplify structure of frequency domain matched filters

通过分析可知，上述简化结构的优点在于实现简单，资源消耗少，但是该结构也有明显的不足，当滤波器系数较短时，滤波器需要补零的位数也随之增加，易引起资源利用率不高[8]。而高速通信系统中，过采样倍数一般较低，滤波器系数也随之较短，采用并行解调架构并不具有优势，因此，在实际应用中还需要对该架构进行改进。

3 定时同步与滤波器的联合实现方案

为解决系统资源利用率不高、避免反馈回路等问题，本文拟从系统结构入手，一方面降低系统复杂度，另一方面减少资源使用。而匹配滤波器作为运算量最大的模块，能否将其通过复用以达到简化成为了本文研究的重点。

3.1 联合结构的提出

通过对图1分析可以知，系统是先完成匹配滤波后再进行同步估计的，可以说不论是在时间上还是资源使用上这两个模块都是完全独立的。同时匹配滤波和定时同步模块都是充分利用频域算法的优势，基于频域实现的，实现过程中都需要用到DFT/IDFT算法，因此在运算过程中如果能够充分利用两个模块间公共的资源，便可以在一定程度上减小不必要的计算。基于该思路，本文提出了一种免混频条件下定时同步与匹配滤波器联合实现的并行解调架构，其解调流程如图3所示。

由图3可得，系统将免混频信号部分调整后，采用重叠保留法的方式，分段将数据送进DFT模块中，然后利用信号的时域卷积特性分别完成I、Q两路的滤波和定时同步工作，最后从恢复时钟的信号中筛选出最佳采样点进行离散傅里叶反变换(IDFT)，并将结果输出到后续的模块中去。该系统利用免混频信号的特殊结构，不仅实现了DFT和定时同步模块间资源的复用，最后还可以通过筛选最佳采样点方式，有效的降低了输出数据速率，为系统硬件资源的节约、复杂度的降低、计算量的减少提供了有效途径。

3.2 联合结构的实现

匹配滤波器与定时同步模块联合实现的关键在于实现模块间资源的复用，也就是将匹配滤波器模块的运算结果复用到定时同步模块中去。基于该思路，本文主要对匹配滤波器模块和同步算法模块进行了改进，以确保通过一次FFT便可实现信号的滤波和同步处理。

3.2.1 DFT模块的改进

在传统架构中，I、Q两路是分开进行处理的，需要两个DFT/IDFT模块和两个滤波器模块，消耗资源较多。在免混频架构中，I、Q两路是混合交替的，若直接做DFT变换，其结果显然无法直接被定时同步模块复用。若对其进行分路、插零、取反后，再做DFT变换，虽然结果可复用，但却带来了运算量和资源上的浪费。因此为减少DFT/IDFT模块和滤波器模块的多次使用，实现DFT模块和定时同步模块的复用，文章利用I、Q两路混合交替的特点，对DFT模块结构进行调整，使得通过一次变换便能得到I、Q两路分别的频域值，具体实现如下。

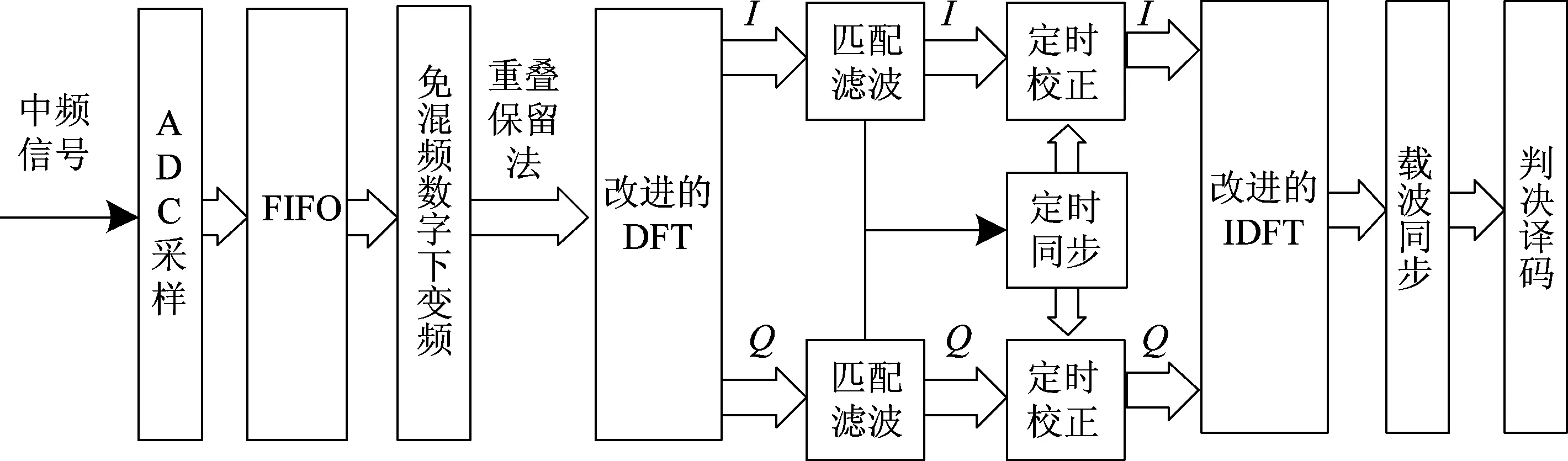
图3 联合结构流程图Fig.3 The flow char of joint structure

假设输入信号为并行的64点免混频信号，采用计算量最小的基- 4 FFT/IFFT算法作为基本架构[9]，64点DFT可表示为：

(5)

记X(k)=X(k2,k1,k0)，x(n)=x(n0,n1,n2)，经分解，式(5)可以表示为：

(6)

其算法实现流程如图4所示。该流程的最小运算单元是4点FFT运算单元，第一级由16组相互独立的最小运算单元组成，第二级由4组4并行的最小运算单元组成，第三级由1组16并行的最小运算单元组成。通过观察可知，在到达第三级之前，基数点(I路)和偶数点(Q路)的处理是相互独立的，也就是说只需要改变第二级与第三级间的级间旋转因子，同时让偶数下标的数进行相加减，让奇数下标的数进行相加减，便可得到序列I(n)=[I(0),I(2),I(4)…]、Q(n)=[Q(1),Q(3),Q(5)…]的FFT结果，最后根据离散信号整数倍内插的性质，可得过低通滤波器后序列[I(0),0,I(2),0,…]，[0,Q(1),0,Q(3),…]的FFT结果。改进后实现流程如图5所示。和DFT模块相似，IDFT模块只需要改变级间旋转因子，并将最小运算单元换成4点IFFT运算单元即可。

3.2.2 同步算法的选择及实现

当前常用的频域同步算法主要有SLN(平方律非线性)、AVN(绝对值非线性)、FLN(四次方律非线性)和LONG(对数非线性)等算法，文献[10]指出，在加性高斯白噪声信道下，四种算法均能够实现大频偏条件下的定时参数估计，其中SLN算法对滚降和信号调制方式相对不敏感，性能相对较稳定。因此基于上述的分析比较，结合文章的高速解调架构特点，本文拟采用SLN算法作为定时同步估计算法。

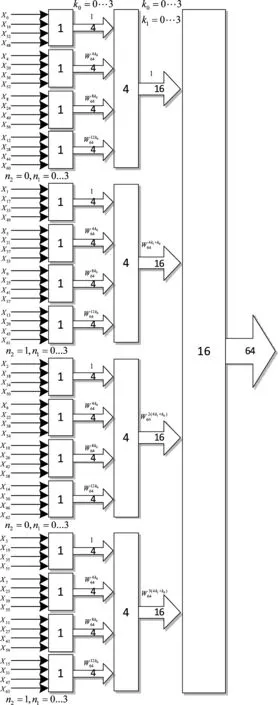
图4 64点基- 4FFT算法流图Fig.4 The flow char of 64-point base- 4 FFT algorithm

通过近似和简化，最终SLN算法中的时延τ可以表示为：

(7)

其中s(n)为输入的免混频信号，T为符号速率，P为一个符号内的采样点数，即P=Ts/T。

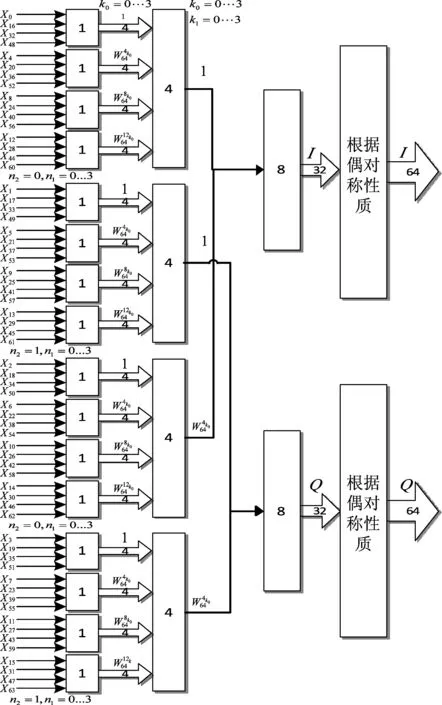
图5 改进后64点基- 4FFT算法流图Fig.5 The flow char of improved 64-point base- 4 FFT algorithm

为满足同步模块对频域滤波结果的复用，需要从频域的角度对式(7)进行理解：|s(i)|2序列在最佳采样点处含有时延信息，时域的传输时延相当于频域频谱分量的相位旋转，因此可以通过将|s(i)|2进行离散傅里叶变化后求得传输时延τ。

(8)

I(n)=[I(0),0,I(2),0,…]

(9)

Q(n)=[0,Q(1),0,Q(3),…]

(10)

由式(8)、(9)、(10)易得：

|s(n)|2=|I(n)|2+|Q(n)|2

(11)

因此可以将序列|s(n)|2频域值求解的问题转化为|I(n)|2、|Q(n)|2频域值求解的问题。利用DFT的频域循环卷积特性和线性性质可得：

(12)

(13)

基于式(13)的思路，式(7)的物理意义最终可理解为，求解序列|I(n)|2+|Q(n)|2以LP为长度的短时傅里叶变换后，第L条谱线的相位值，也可以看作对序列|I(n)|2+|Q(n)|2做P点短时傅里叶变换后，对第1条谱线做L个周期的平均统计。而DFT[I(n)] 和DFT[Q(n)]均已求得，可以直接将运算结果运用到定时同步模块中去。而后将求出的时延通过相位旋转因子的形式，在频域完成输入序列的时延校正，最后再将恢复结果通过IDFT反变换，输出到下一步的处理流程中。

由此分析可得SLN算法的频域并行实现结构如图6所示。对匹配滤波器输出的I/Q各32路的信号进行循环卷积计算，求得第L条谱线的值，而后对所求的相位角进行算数平均便得到定时误差的估计值。和传统的时域并行实现结构相比(如图7所示)，完成一次32路并行的数据的处理，频域并行算法大概需要1次乘法、1次加法以及1次相位求解的时钟周期，而时域并行的算法大概需要1次乘法、4次加法以及1次相位求解的时钟周期。由此可得，采用频域并行结构并不会带来系统上的时延。

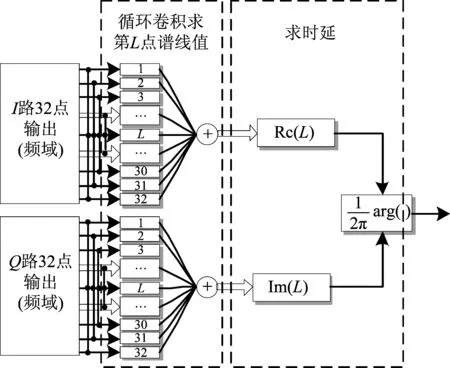
图6 SLN算法频域并行实现结构Fig.6 SLN algorithm frequency domain parallel implementation structure

图7 SLN算法时域并行实现结构Fig.7 SLN algorithm time domain parallel implementation structure

4 性能仿真与分析

4.1 算法性能仿真与分析

利用MATLAB软件，对估计量的均方误差和信号解调前后的星座图进行仿真分析。仿真中采用QPSK信号，信号符号速率为600 Msps，采样率为2.4 GHz，中频信号频率为600 MHz，每个符号4个采样点，发送端和接收端采用的滚降系数均为0.35的33阶根升余弦滤波器。

仿真中估计性能由传输时延τ的均方误差和时延恢复前后的信号星座图来描述。假设信号的传输时延分别为T/8和3T/8，观察长度为64个符号时，在不同信噪比下联合算法的估计性能和修改后克拉美罗界(modified Cramer-Rao bound,MCRB)对比如图8所示。

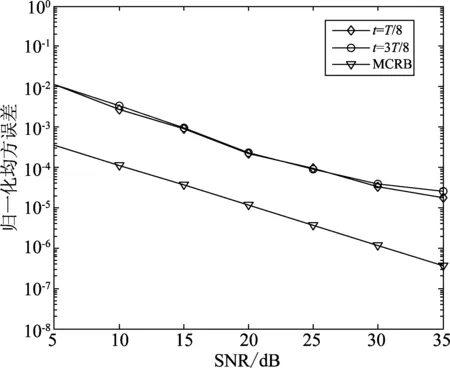
图8 不同信噪比条件下的均方误差Fig.8 Mean square error at different SNR

图8是在不同信噪比条件下，不同定时估计的均方误差曲线与修正克拉美罗界间的比较。由图8可以看出，在加性高斯白噪声信道下，大时延和小时延的均方误差线基本重合，联合较为接近克拉美罗界，说明该算法对大时延和小时延都具有较好的估计性能。

图9显示了在0～14 dB的信噪环境中文中算法与Gardner算法的误比特性能，由图可以看出，在信噪比为6～14 dB时Gardner算法具有较低的误码率曲线，其中在误比特率为10-4时，文中算法较Gardner算法有约0.5 dB的性能损失。在实际应用中，虽然Gardner算法精度高，但是估计时延长，不适合实时信号处理，而文中算法无反馈回路，即便精度差点也是可以接受的。

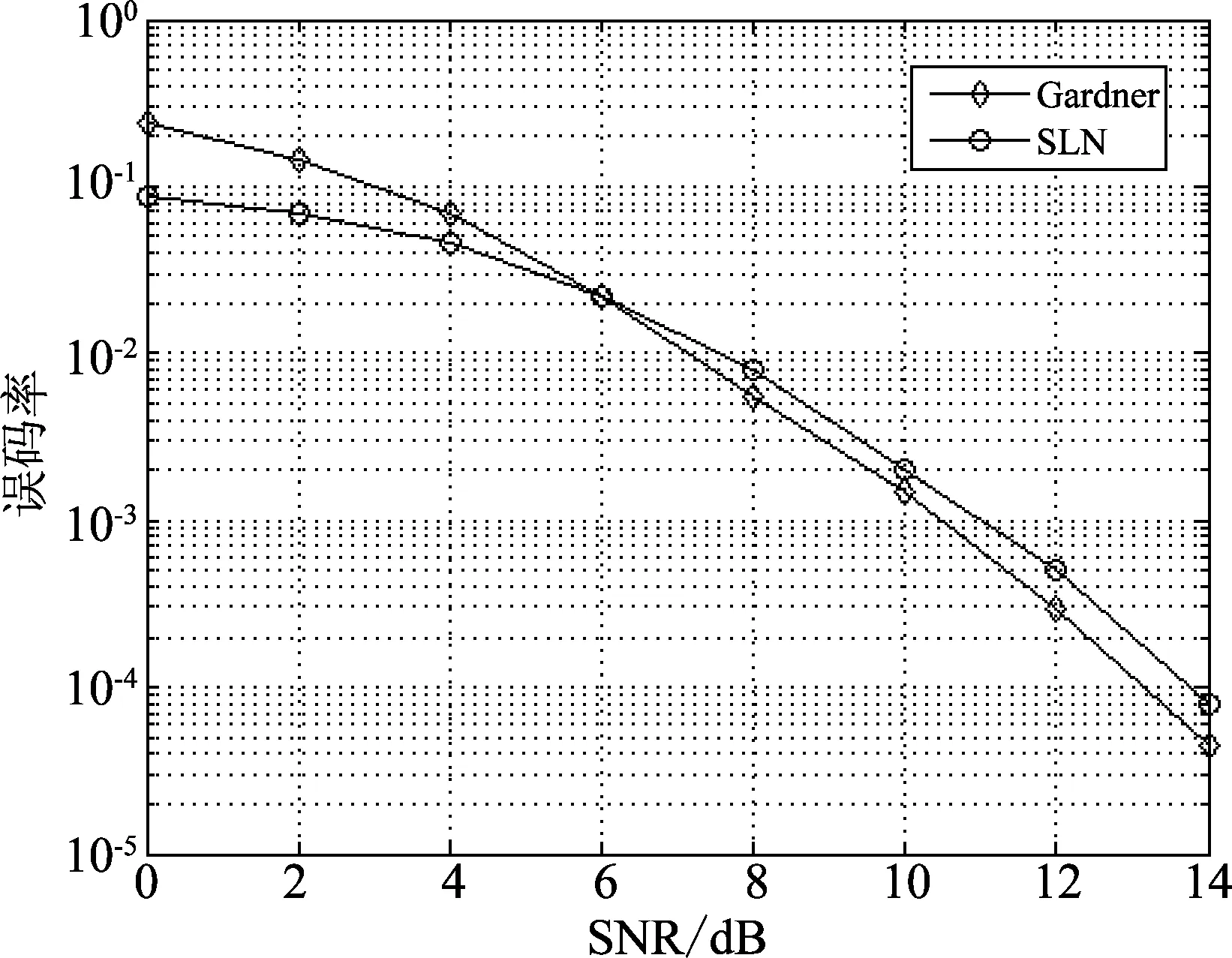
图9 Gardner算法与SLN算法误码率仿真Fig.9 The BER simulation of Gardner algorithm and SLN algorithm

图10(a)～(d)给出了时延误差为T/8和3T/8、信噪比为25 dB时接收信号时延恢复前后的星座图。图10(e)～(f)给出了时延误差为3T/8、信噪比为15 dB时接收信号时延恢复前后的星座图。

从图10(a)～(d)可以知，在信噪比为25 dB的大时延环境下，接收端的相位信息基本被破坏，已经完全看不到4个基准相位点了，但是经过时延恢复后，可以明显的看出基准相位点，可见该算法在信噪比较好的解调环境中能够准确的实现时延恢复。从图10(e)～(f)可以看出在低信噪比、大时延的解调环境中，信号基准点已经完全模糊不清，但是该算法依旧有较好的时延恢复性能，能够较准确的恢复时延信号，说明该算法适用于低信噪比的通信环境。

图10 信号星座图Fig.10 Signal constellation

4.2 方案复杂度分析

本文并行解调架构的特点在于通过资源的复用有效降低了系统实现的复杂度、减少系统资源的使用，相对于其他解调架构具有一定的优势。为进一步量化说明，拟通过不同解调方案乘法运算的次数为比较标准，分析不同方案的运算量。选择方案如下：

方案1 Gardner定时同步算法(闭环算法)+FIR滤波器。该结构主要包含匹配滤波器、内插滤波器、定时误差检测器、数控振荡器(NCO)和环路滤波器等。为方便比较，假设系统中匹配滤波器、内插滤波器和本文的滤波器阶数相同，均为M阶，同时忽略NCO和环路滤波器等较小的部件的运算量，因此得到方案的运算量如表1所示。

方案2 最大平均功率定时同步算法(开环算法)+FIR滤波器。该结构主要包括平均功率计算模块和匹配滤波器模块，算法均基于时域实现。

方案3 SLN同步算法+FIR滤波器(FFT实现)。该结构主要包含定时同步模块和匹配滤波器模块，其中同步模块基于时域实现，使用时域乘法运算，匹配滤波器模块基于频域实现，使用复数乘法运算。由于输入信号均为实数，因此可以根据实信号的傅里叶变换具有共模偶对称性，降低一半的运算量[11]。为方便比较，按照一次复数乘法等价于3次实数乘法快捷方式进行换算[12]，最终可得该结构的运算量。

方案4 定时同步与匹配滤波器联合实现。方案中匹配滤波器计算方式和方案3的类似，不同的是方案中将定时同步嵌入到滤波器模块中去，因此在定义模块计算量时，可以将其分别等效为总运算量的1/2。

表1给出了四种方案所需要的乘法器次数的估量值。

表1 不同方案所需要乘法运算次数比较

假设码元的长度L=512，分成m=64段，系统采用P=4倍过采样，滤波器阶数M=33，利用重叠保留法对数据进行分段处理，每段长度为64点，滤波后长度为N=64。

从表1可以看出，方案1和方案2计算量差别不大，因此在选择时主要考虑同步算法的精度和适用场合。方案3相比于方案1和方案2，滤波器的计算量减少明显，说明简化后的匹配滤波器不论是在硬件资源使用上还是实现复杂度上都有较大的改进。方案4通过模块的融合，极大的减少了系统计算量。和方案1相比，方案4的计算量大约是方案1计算量的30%，说明该方案适用于高速场合。