城市公交线路模态行驶工况构建研究*——以西安市公交线路为例

李耀华 苟琦智 任田园 邵攀登 宋伟萍

(长安大学汽车学院 西安 710064)

0 引 言

汽车行驶工况是用来描述特定交通环境下车辆行驶特征的速度-时间历程，对汽车领域的相关研究有着重要作用，是汽车研发、试验和检测重要的数据支撑。根据行驶工况形态，可以分为瞬态工况和模态工况2种。瞬态工况典型代表有美国行驶工况(FTP75)，模态工况典型代表有NEDC工况、Japan10-15工况和中国城市客车四工况等。目前，瞬态工况的构建方法较为成熟，有聚类分析法、V-A矩阵法和马尔科夫链法等[1-6]。但汽车模态行驶工况构建方法相关研究较少。其中荆哲铖[7]认为模态工况特征在于曲线形态规则，以片段最短持续时间和相邻片段加速度差作为依据，运用最小二乘法将瞬态工况曲线进行模态化处理；张鹏运[8]用小波去噪理论进行瞬态工况模态化研究。以上研究主要是运用数学手段将瞬态工况转成模态工况，最终生成的模态曲线形态依然较为复杂，可操作性差。

基于西安市公交线路实测运行数据，运用多目标理论优化方法构建出公交线路模态工况，并通过特征值误差和比功率分布对其进行验证。结果表明，本文构建的模态工况能真实反映西安市城市客车实际运行状态，构建模态工况的方法具有一定的科学性和准确性，从而为开发出曲线规则、操作性强、精度高的模态工况奠定理论基础。

1 数据采集与处理

1.1 线路筛选

目前，西安市公交线路达到近200条。定义线路强度用来量化线路的代表性[9-11]，见式(1)。

(1)

式中:μi为第i条线路的线路强度；λj为第i条线路第j个站点出现的总频数；n为第i条线路的总站点数。

西安市公交线路筛选综合考虑线路代表性和覆盖率。通过对西安市所有公交线路线路强度统计，得到市区和市郊公交站点强度最大的前5条线路，见表1。

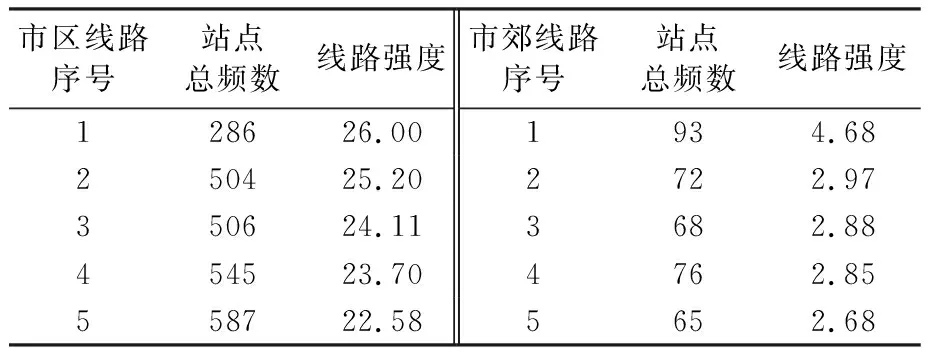
表1 西安市区市郊线路强度前5条线路Tab.1 Xi′an urban and suburban lines with top 5 line intensity

综合考虑线路走向、覆盖率和线路强度。选取市区排名第2和第5的线路，市郊排名第1的线路进行数据采集，其测试公交路线见图1。

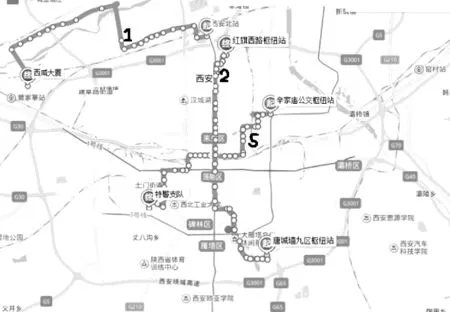
图1 测试公交路线图Fig.1 Test bus route map

1.2 数据采集

数据获取方法是在市区和市郊3条线路上共随机挑选9辆正常营运的新能源公交车安装GPS+CAN采集设备，进行全天不间断数据采集。数据采集周期为15 d，采样时间保证覆盖运营时间、上下班高峰和节假日，同时采样过程充分考虑驾驶员随机性和天气因素[1-9]。车载设备的采样频率为1 Hz。经过1个周期的数据采集，最终市区线路2采集数据量为544 700条有效车速信息，市区线路5采集数据量为526 850条有效车速信息，市郊线路1采集数据量为498 610条有效车速信息。

1.3 数据预处理

由于采集方法限制和GPS设备因素，会导致采集的数据出现漂移和失真[9-13]。因此，需对采集的数据进行预处理。数据预处理流程见图2。

图2 数据预处理流程
Fig.2 Data preprocessing process

在正常的公交车运营过程中，定义将最大加速度上限设定为3 m/s2，最大减速度上限设定为-3 m/s2。因此，加减速度超过限值的数据点为尖点。采用线性插值的方法处理尖点数据。GPS采集数据存在零点漂移现象。采用CAN总线车速标定方法处理零点漂移。即采用仪表盘CAN总线怠速数据对GPS怠速数据进行标定。

定义公交车从首站到末站行程为1个长行程。由于采样设备输出数据为以天为单位的连续采样数据，且采样数据包含汽车站内行驶和来回公交公司等无效数据，因此，将公交车从首站到末站的长行程数据从连续数据中剥离出来，以最大程度保证数据的有效性。首先以怠速时间进行初步截取，时间尺度依据实际公交调度时间为准；运营高峰期时，公交到站停车时间很短，因此以运行距离为标准进行二次截取；最后剔除长度过小的无效长行程。

1.4 样本数据库建立

采集3条公交线路数据，如何利用不同线路数据建立样本数据库以用于研究西安市公交模态工况也是笔者研究的问题之一。以线路强度比决定数据库中线路数据量占比。以市区2条线路为例，线路2和线路5的线路强度比为1.12，因此，线路5取40个长行程，线路2取45个长行程建立市区样本数据库。市郊线路1取40个长行程构建市郊样本数据库。按照此方法建立同样数据量验证数据库以用于对建立的模态工况有效性进行验证。市区和市郊线路总样本特征值见表2。

表2 市区、市郊线路总样本特征值比较Tab.2 Comparison of urban and suburban sample Eigenvalues

2 模态工况构建

2.1 模态工况模型

汽车在实际道路上运行，通常可简化为加速、减速、匀速和怠速4个工况。参照ECE-EUDC工况，将市区线路模态工况简化为图3模型，并设置17个时间变量和7个速度变量。将市郊线路模态工况简化为图4模型，并设置12个时间变量和7个速度变量。

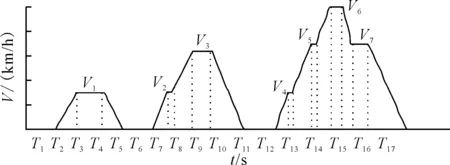
图3 市区线路模态工况模型图Fig.3 Mode of urban circuit modal condition

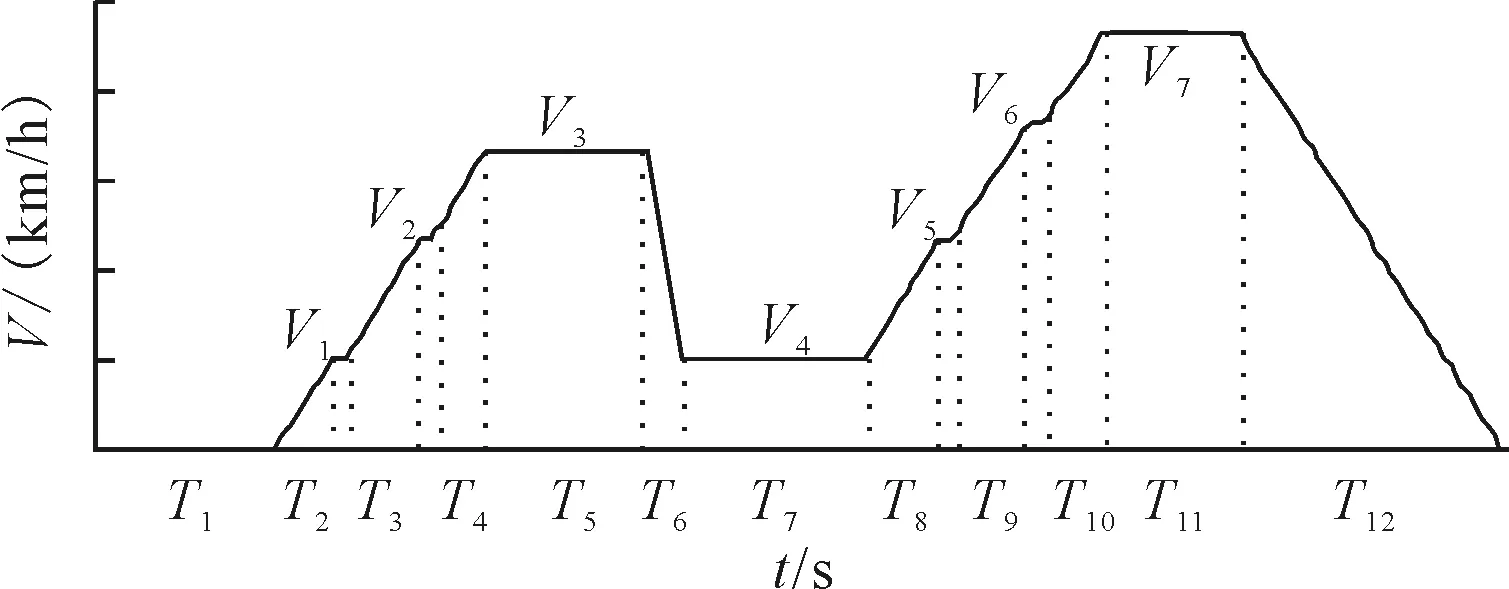
图4 市郊线路模态工况模型图Fig.4 Mode of suburban circuit modal condition

2.2 模态工况模型解析

由图3可见，市区线路模态模型需要对其各个运行段的运行时间及运行车速共24个变量进行优化。优化变量可表示为

X1=(T1,T2,…,T17,V1,…,V7)

(2)

X2=(T1,T2,…,T12,V1,…,V7)

(3)

运用多目标优化理论对模态工况模型求最优解，选取怠速比例FPmi、加速比例FPma、匀速比例FPmc、减速比例FPmd、平均车速FVm、平均运行车速FVmr、平均加速度Fam、平均减速度Fdm等8个具有统计意义的重要指标作为目标函数优化计算[8-10]，故确定目标函数见式(4)～(13)。

(4)

Fpma=

(5)

Fpmc=

(6)

(7)

(8)

(9)

(10)

(11)

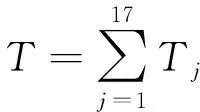
(12)

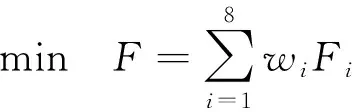
(13)

上述公式中S为运行距离，即为图3中图形面积；Fi为8个具有统计意义的重要指标；wi为以上8个分目标的权因子；Pi，Pa，Pc，Pd，Vm，Vmr，Am，Dm分别为实验总样本数据的怠速比例、加速比例、匀速比例、减速比例、平均车速、平均运行车速、平均加速度和平均减速度。

结合市区线路总样本特征参数。定义市区模态模型目标函数的约束条件见式(14)。市区线路模态最高车速为50 km/h，最大加、减速度均不超3 m/s2，换挡点车速均在15，35，50 km/h左右。

(14)

市郊模型目标函数和约束条件的构建原理与市区模型一致。根据样本最高车速及公交公司相关限速规定，本文定义市郊线路模态最高车速为55 km/h。

2.3 模型优化求解

现对以上模型目标变量进行求解，由于以上目标函数的8个变量都反映了汽车行驶工况的重要特性，具有平行关系，故而本文给八个重要指标加权wi将多目标转化为单目标求解。由于以上8个指标分别从速度、速度分布、加速度方面描述所开发的工况，故本文认为其重要性相当，取其权因子相等,即wi=0.125 (i=1,2,…,8)。

对目标函数和约束条件进行多目标优化，通过计算机编程，运用Matlab优化工具箱，并对时间圆整，得到市区和市郊线路模态工况的各个参数优化解X1和X2，优化解向量为

X1=(18,14,11,14,18,6,12,8,13,18,6,11,9,

5,9,8,14,15,14.94,35,14.9,34.9,50,35.1);

X2=(22,8,11,8,15,6,39,12,10,3,9,

32,14.9,35.1,49,15,35.02,50.06,55)。

依据优化结果，合成的市区线路(简称UB-MD)和市郊线路模态工况(简称SUB-MD)分别见图5～6。市区、市郊线路模态工况特征参数见表3。

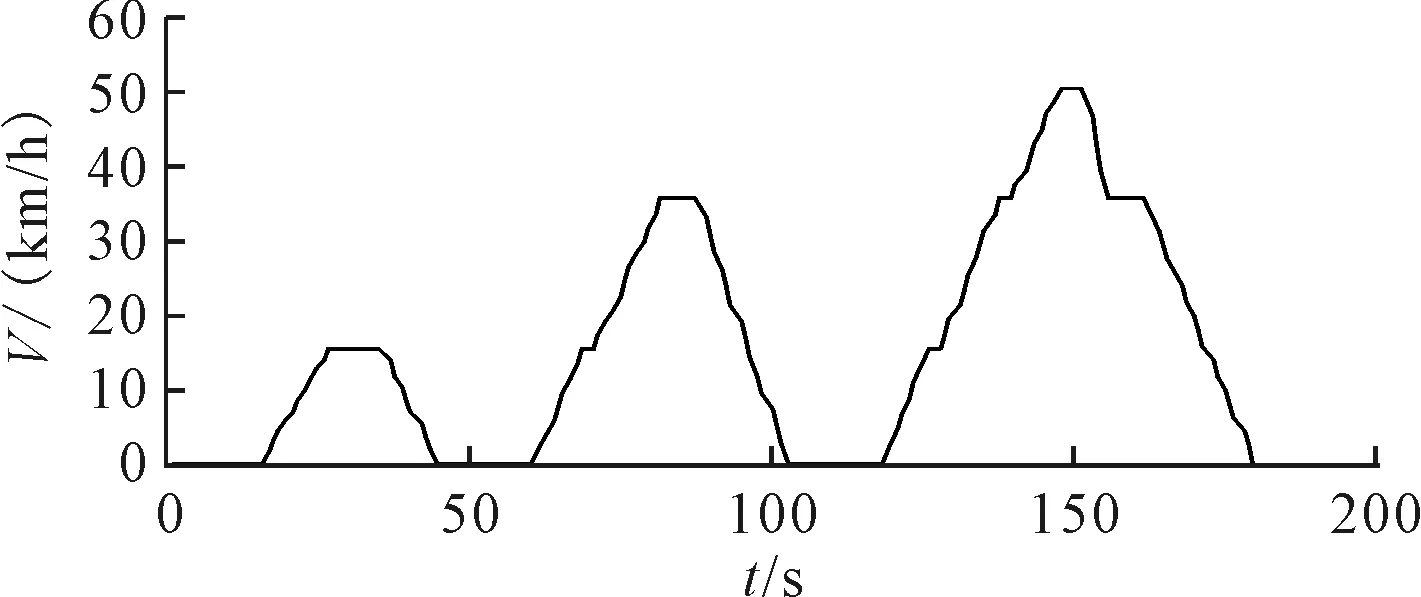
图5 市区线路模态工况Fig.5 Modal condition of urban circuit

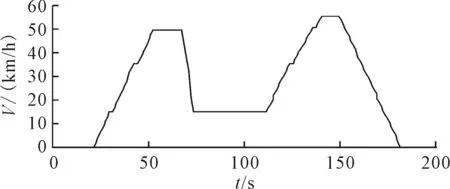
图6 市郊线路模态工况Fig.6 Modal condition of suburban circuit

3 工况验证

3.1 特征值误差验证

为对所构建的西安市城市客车行驶工况做出评价，选取Vmean，Vmr，Vsd，Amean，Dmean，Asd，Pa，Pd，Pc，Pi共10个影响比较大且具有统计意义的特征参数进行误差评估[9-13]。各指标误差和平均误差计算见式(15)～(16)，误差计算结果见表3。

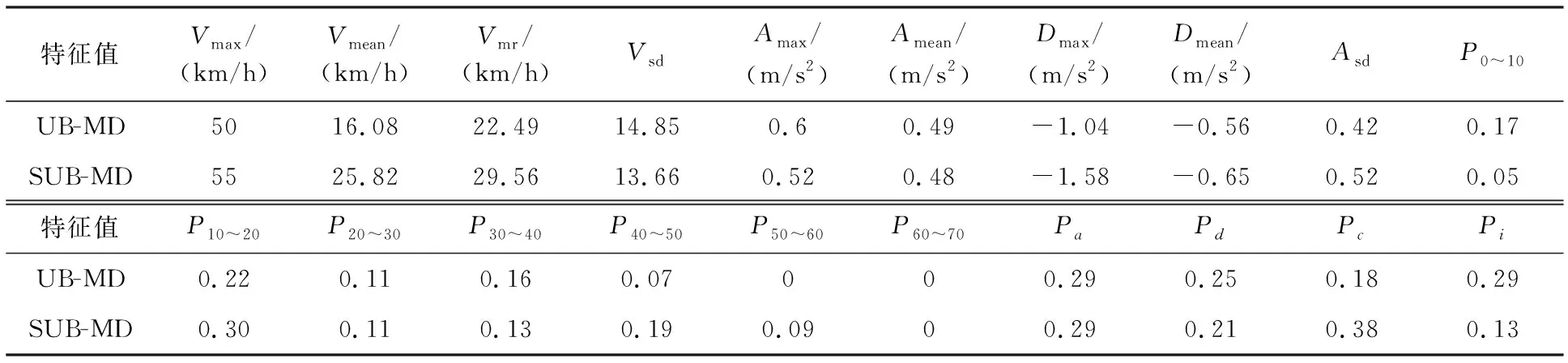
表3 模态工况特征值比较Tab.3 Comparison of modal conditions Eigenvalues

(15)

(16)

相对误差验证以模态工况、城市客车用运转循环工况(CCBC)，ECE-EUDC工况与验证样本的相对误差对比进行分析，如表4所示。西安市市区线路模态行驶工况与样本平均误差最小，为8.54%；城市客车用运转循环工况(普通路)误差为14.25%；ECE-EUDC市区工况误差最大，为28.44%。市郊线路模态行驶工况与样本平均误差仅为2.77%，城市客车用运转循环工况(快速路)误差为27.42%，ECE-EUDC市区工况误差达到61.18%。误差对比分析表明城市客车用运转循环工况和ECE-EUDC工况与总样本数据误差较大，不能反映西安市城市客车实际运行工况，而笔者构建的模态工况能真实反映西安市城市客车实际运行状态，且构建模态工况的方法具有一定的科学性和准确性。

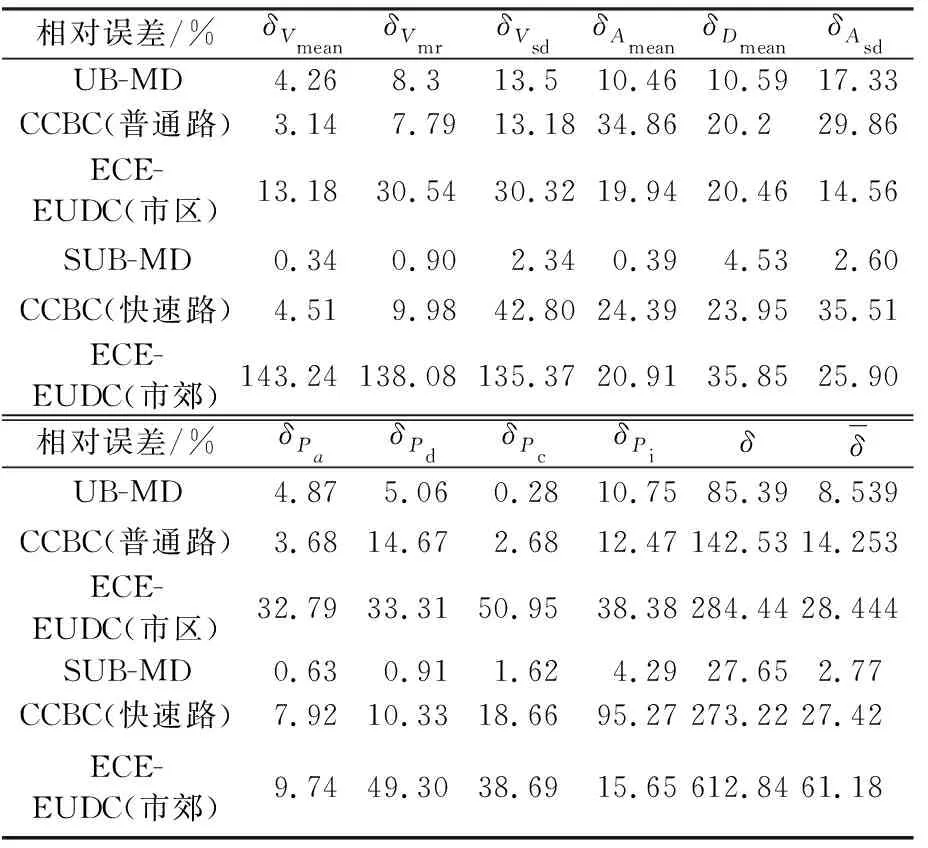
表4 模态工况、城市客车循环工况、ECE-EUDC工况与验证样本相对误差分析Tab.4 Relative error analysis between modal conditions,CCBC, ECE-EUDC and verification samples

3.2 比功率分布验证

比功率参数(vehicle specific power，VSP)既能反映车辆旳行驶特征，又与车辆排放密切相关[14-17]，因此，利用比功率分布进行工况验证。西安市新能源公交车VSP的计算公式见式(17)。以1 kW/t作为VSP划分区间间隔。

VSP=v×(a+0.091 99)+0.000 171×B3

(17)

将模态工况、典型工况和验证样本计算VSP参数，并进行区间划分，得到市区和市郊线路比功率分布见图(7)～(8)。

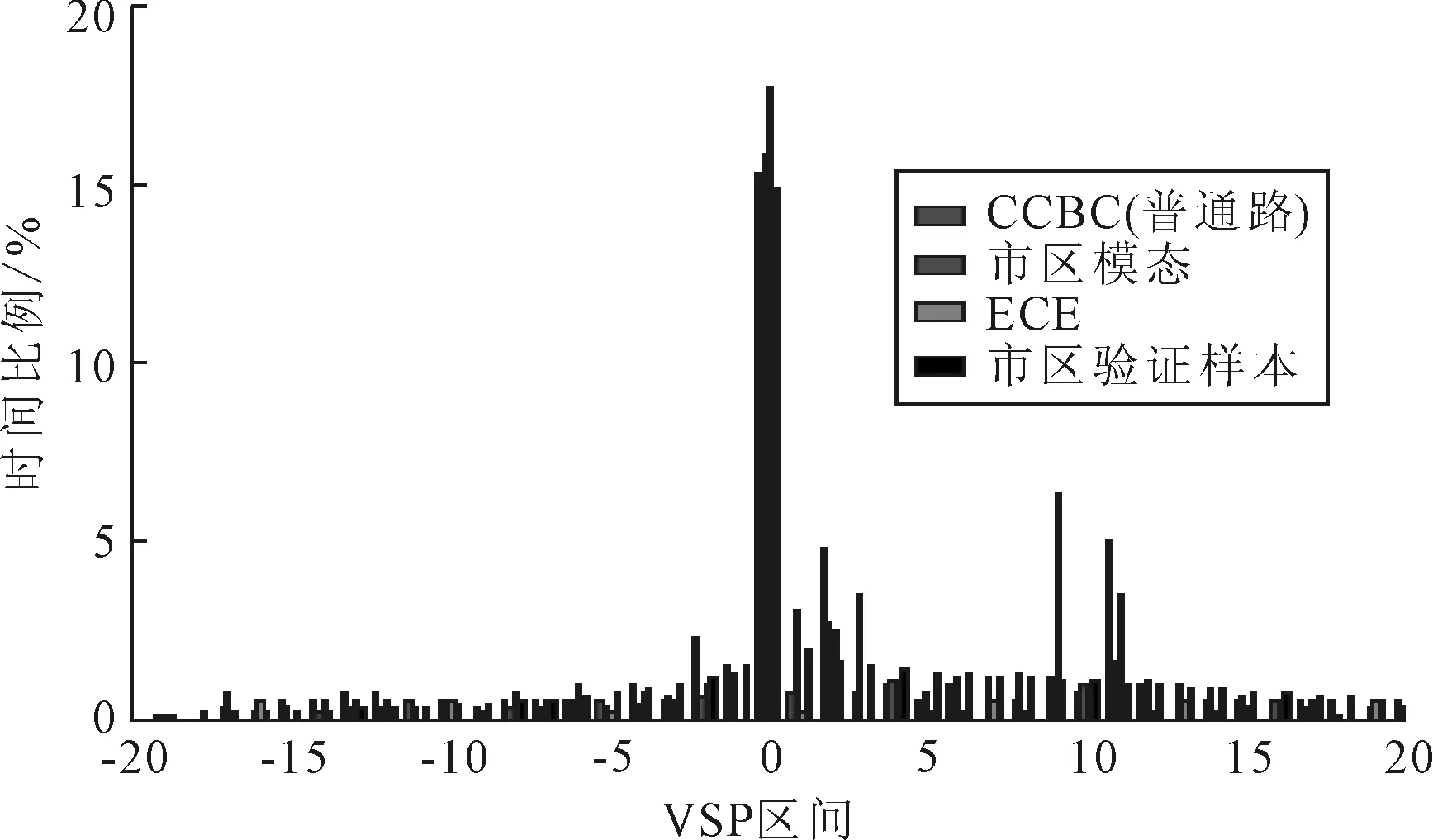
图7 市区模态、CCBC(普通路)、ECE工况与市区验证样本数据的比功率分布对比图Fig.7 Comparison of specific power distribution between urban modal condition,CCBC (normal road),ECE and urban verification sample data

图8 市郊模态、CCBC(快速路)、EUDC工况与市郊验证样本数据的比功率分布对比图Fig.8 Comparison of specific power distribution between suburban modal condition, CCBC (highway),EUDC and suburban verification sample data

为直观表述VSP分布的相似性，选取均方根误差RMSER衡量指标。RMSE值越小，则该工况与验证样本的VSP分布相似度越高[16-18]。RMSE计算公式见式(18)。计算可得工况与验证样本的比功率分布误差，见表5。

(18)

式中：i为VSP区间编号；Bins,i为样本编号为i的VSP区间分布比例；Binmic,i为工况编号为i的VSP区间分布比例；N为区间总数。

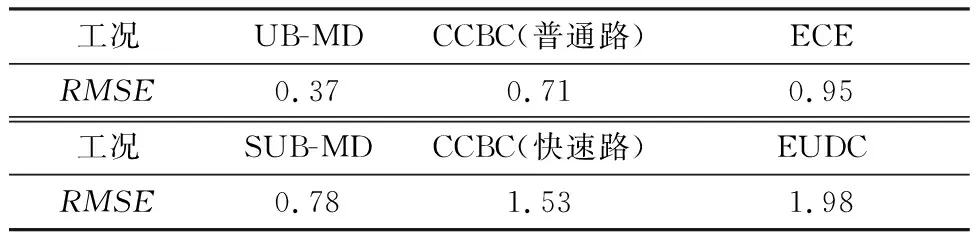
表5 工况与验证样本RMSER值比较Tab.5 Comparison of RMSER values between drivingconditions and verification samples

依据比功率分布相似性可知，笔者建立的市区模态、CCBC(普通路)和ECE与市区验证样本比功率分布误差分别为为0.37%，0.71%和0.95%。市郊模态、CCBC(快速路)和EUDC与市郊验证样本比功率分布误差分别为0.78%，1.53%和1.98%。本文建立的模态工况与验证样本比功率分布误差较小，表明建立的模态工况能准确地预测公交车的排放。

4 结束语

通过线路筛选，利用GPS+CAN设备采集大量实测数据。基于总样本数据特征参数确定目标函数及约束条件，运用多目标优化理论求解参考模型关键点参数，建立西安市区和市郊线路模态工况。

特征值误差验证可知，市区和市郊线路模态工况与验证样本平均误差最小，分别为8.54%和2.77%；城市客车用运转循环工况和ECE-EUDC工况与样本平均误差均超过10%。笔者建立的模态工况在数理分析角度更符合实测数据。

比功率分布验证可知，构建的市区和市郊模态与验证样本比功率分布误差为0.37%和0.78%。而CCBC工况和ECE-EUDC工况与验证样本比功率分布误差较大，这表明本文建立的模态工况在排放预测角度更符合实测数据。

关于模态工况构建研究，目前尚无更好的方法，以参考模型为基础，探索了一种基于实测数据优化模型关键数据参数的构建方法。该方法对于样本数据精度要求较高，优化算法具有多样性，但参考模型未有统一标准。在优化算法和参考模型选择方面值得进一步研究。