基于GIS的住宅价格时空分布规律研究

文/张靖苗、李利芬 云南城市建设职业学院 云南昆明 650222

1、引言

随着我国住房制度改革的不断深入，房地产业呈现出高速发展的态势，房价更是成为社会各界和专家学者们关注的焦点。由于房地产与一般商品有所不同，它作为一个具有空间属性的商品，其价格变动深受地理区位因素的影响而具有明显的空间性。也就是说，在一个城市中，位于不同区域的房地产价格水平不同，使得房地产价格具有区域差异，即房价的空间分异。本文利用ARCGIS作为技术支持，通过空间自相关分析法和空间插值法来研究成都市住宅价格的时空分布规律。

2、数据与研究方法

2.1 数据采集与处理

本文选择成都市主城区作为研究区域，以二手房市场为研究对象，原因是相对于新开盘的项目，二手房的市场化程度更高。其次，住宅市场的众多物业类型中，普通商品房的比重较大，所以本文选取的住宅样本均为普通商品房。数据主要来源于成都市搜房网和安居客，收集样本总量为1500个，选择2015年6月和12月的普通住宅小区二手房销售均价作为价格数据。以这些住宅小区的名称、位置、销售均价等数据为属性数据，通过ARCGIS建立空间数据库，把成都市地图作为分析底图，矢量化后构建样本住宅的点数据图层。将属性数据与底图匹配，得到成都市2015年普通住宅分布图（图1）。

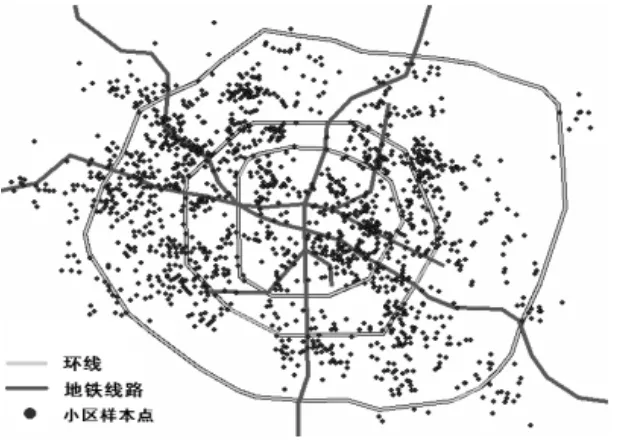
图1 成都市2015年普通住宅分布图

2.2 研究方法

2.2.1 空间自相关分析

在空间统计分析中，通过相关分析可以检测两种现象（统计量）的变化是否存在相关性。空间自相关分析就是量测所谓空间事物的分布是否具有自相关性，高的自相关性代表了空间现象聚集的存在[1]。空间自相关可分为全局空间自相关和局域空间自相关，全局空间自相关可以用来描述某现象的整体分布状况，以及空间中相似属性的聚集程度；局域空间自相关可以帮助我们更加准确地把握空间要素的异质性特性，并推算出聚集地的空间位置和范围。其中Moran's I值是应用较为广泛的空间自相关性判定指标，全局空间自相关Moran's I计算公式如下:

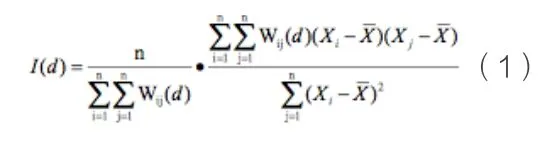
局域空间自相关Moran's I计算公式如下:

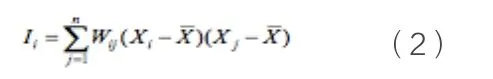
其中，n为研究对象的数目，Xi和Xj为观测值，为 X的平均值。Wij为区位相邻矩阵，它是（0，1）空间权重矩阵，权重矩阵可以通过邻近规则和距离规则来构建。Moran's I值介于-1与1之间，I＞0，表示空间正相关，说明相邻区域有相似的数据属性，空间实体呈聚合分布；I＜0，表示空间负相关，说明相邻区域属性差异大，空间实体呈离散分布；I=0则表示空间实体是随机分布的，且I值越大表示空间分布的相关性越大[2]。

2.2.2 空间插值法

在实际研究中，我们无法对空间中所有的点进行观测，但可以通过设置一些关键样本点来反映空间分布的全部或部分特征，然后利用空间内插的方法来获取未采样点的值[3]。也就是说，根据已知点数据来估算研究区内未知点数据值的过程就是空间插值。本文选取空间插值中的克里金插值法（Kriging），此方法是建立在变异函数理论及结构分析基础上，在有限区域内对区域化变量的取值进行线性无偏最优估计的一种方法[4]。

本研究中采用的是普通克里金插值的方法，估算任意点Z值的通用方程如下：

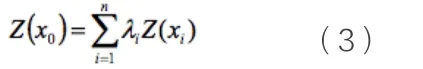
3、实证研究

3.1 房价空间自相关检验

为反映出相邻区域内住宅价格之间的相互影响关系，本文通过探索性空间数据分析（ESDA）中的空间自相关性分析方法，从根本上概括了成都市普通住宅二手房房价的空间集聚与分散的结构模式，并能够定量检测空间集聚现象的存在。

3.1.1 房价分布的全局空间自相关分析

利用ARCGIS计算得到成都市2015年6月和12月的普通住宅二手房价的全局Moran's I指数（表1），分别为0.4252和0.4087，均大于1，且Z统计量分别为32.33和31.08，因此成都市普通住宅二手房价格整体上存在显著的正向空间自相关性，空间上集聚分布现象明显，即房价高的区域和房价低的区域都有集聚现象。6月份的莫兰指数较12月份的略高，但相差不大，说明这种相关性比较稳定。

3.1.2 房价分布的局域空间自相关分析

通过ARCGIS的聚类和异常值分析(Anselin Local Moran's I)功能得到Local Moran's I指数（图2）。住宅样本价格之间存在四种关联模式，正向和负向的空间关联模式各有两种。其中正向的空间关联模式包括：①局部高值空间聚类（“高-高”聚类），即价格高于总体均价的区域单元被同是价格高于总体均价的区域单元所包围。从图2可以看到，此类住宅样本大部分集中在成都市的一环以内，即中心城区，还有一部分集中在西二环以外以及南二环以外。②局部低值聚类（“低-低”聚类），即价格低于总体均价的区域单元被同是价格低于总体均价的区域单元所包围，这类住宅样本主要分布在成都市的北部二环以外。处于这两种关联模式下的样本点数量越多，住宅价格的空间集聚性就越显著。负向的空间关联模式包括：①局部高值异质点类型（“高-低”聚类），表示某一区域单元价格高于总体均价，但其周围单元价格低于总体均价，此类样本点主要分布在成都北部，一环与三环之间，主要集中在地铁站附近，说明地铁对周边房价是有一定影响的。②局部低值异质点类型（“低-高”聚类），表示价格低于总体均价的住宅样本点被价格高于总体均价的点所包围，这类样本点数量较少，大部分集中在一环内，少部分在西边二环与三环之间，这类样本点主要位于在中心城区的城中村附近，周边环境相对较差，导致房价偏低。

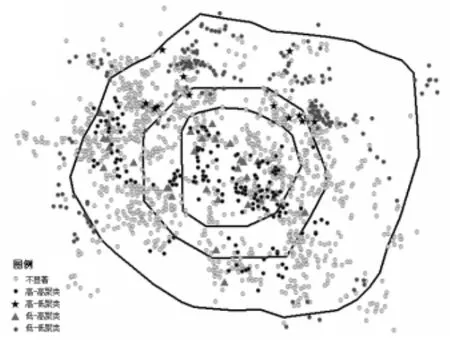
图2 （a）成都市6月份住宅价格聚类分析图

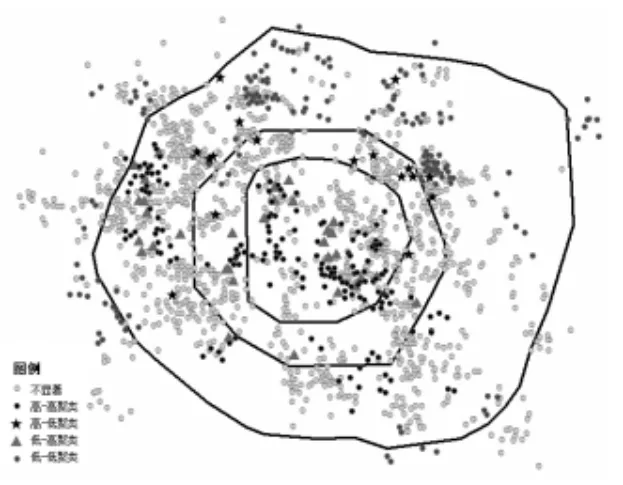
图2 （b）成都市12月份住宅价格聚类分析图

3.2 房价时空分布特征

本文利用ESDA对样本数据进行趋势分析，并利用ARCGIS对样本点进行空间插值，绘制等值线图，以此来研究成都市的时空分布特征。

3.2.1 趋势分析

对房价数据进行趋势分析，可以揭示房价整体在空间区域变化的主要特征，从而反映出房价空间的整体规律。利用ARCGIS的趋势分析功能，将成都市6月和12月的房价数据分别绘制成趋势分析图（图3）。图3中的X轴表示东西方向，Y轴表示南北方向，Z轴表示小区均价，曲线为小区均价在各方向上的投影所形成的趋势线。从图上可以看到，房价趋势线在东西方向上和南北方向上都是倒U形状，呈现中间高、两边低的趋势，且北边的房价明显低于南边，西边的房价高于东边，与以前形成的“南富西贵，北乱东穷”的特征相符。其中12月的房价分布在正南方向和正西方向较6月份有所抬高，但整体的趋势变化不大。

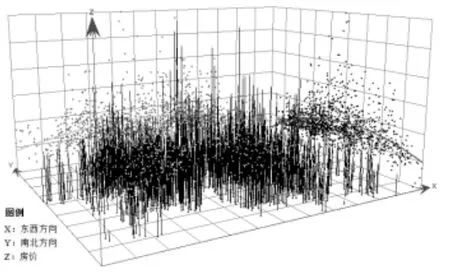
图3 a成都市6月房价趋势分析图

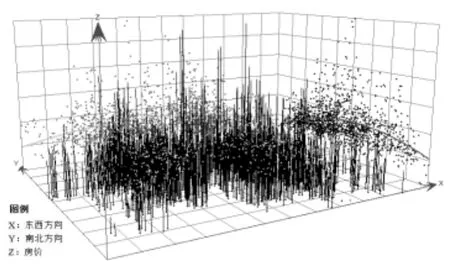
图3 b成都市12月房价趋势分析图

3.2.2 房价空间分布特征探析

本文采用普通克里金插值法对成都市普通住宅小区二手房价格进行插值，得到房价的空间分布图，再利用等值线分析模块绘制房价等值线图（图4）。图中左下角为图例，表示房价的范围，颜色越深说明房价越高。加粗的黑线为环线位置，其余闭合曲线为房价等值线。从两张图中可以看到成都市房价空间分布具有以下特征：

①在部分区域，房价呈现自中心向四周逐渐降低的趋势，房价峰值区域位于一环的中西部，房价大致在17000元/m2～23000元/m2（6月）和16700元/m2～22000元/m2（12月）之间，由此处向四周递减。结合成都市的实际情况来看，一环中西部有青羊宫和杜甫草堂等几个比较著名的旅游景点，对周边房价起到了带动作用。

②天府广场一带是成都市的市中心，也是传统的城市CBD，但房价的最高值并不在这一区域，而是集聚了一些中高档小区，房价在13500元/m2～17000元/m2（6月） 和13300元/m2～16700元/m2（12月）之间。说明在成都市这样的大城市，传统的商务中心可能已经不再被认为是居住条件最好的区域。城市基础设施建设及城市功能的完善，为城市居民提供了更多的选择。

③从等值线图的颜色深浅可以看到，除了一环以内的中心区域颜色最深外，在二环与三环之间的西部和东南部颜色也较深，表现跳跃。说明成都市的房价分布存在明显的空间异质性，且房价分布不连续。西部表现跳跃的有金沙片区和光华片区。东部表现跳跃的是建设路片区、万年场片区和锦华商圈片区。

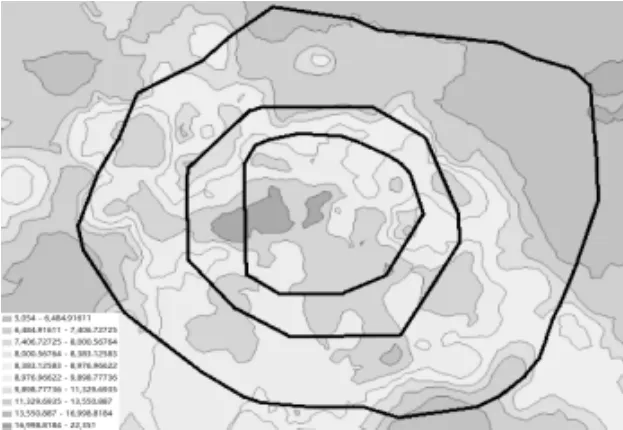
图4a 成都市6月住宅价格等值线图

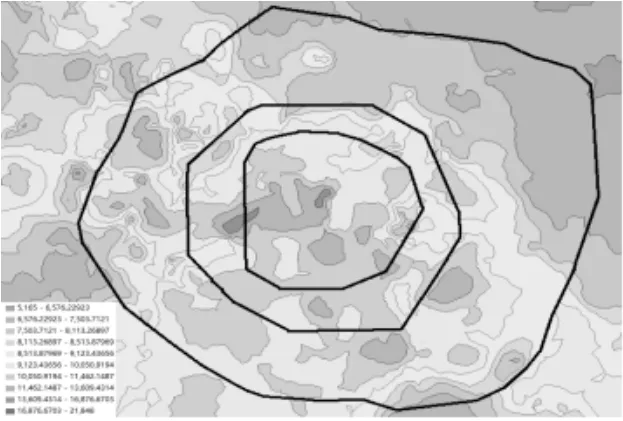
图4b 成都市12月住宅价格等值线图

结论：

本文利用ARCGIS软件的空间分析功能，揭示了成都市普通二手住宅价格的时空分布特征。结果表明：

①成都市2015年6月和12月的普通二手住宅价格的全局Moran's I指数均大于0，说明成都市二手房房价存在正向空间自相关性，总体上呈现出空间集聚的特征。其中，大部分房价表现为局部空间集聚，而少量存在空间异质性，即呈现离散分布。房价的局部高值空间聚类集中在成都市的一环以内，还有一部分集中在西二环以外以及南二环以外，低值聚类主要分布在成都市的北二环以外。存在空间异质性的区域主要分布在中心城区的城中村附近，以及成都北部，一环与三环之间的地铁站附近，说明周围的居住环境和轨道交通对房价存在一定的影响。

②成都市二手住宅价格的地域分异规律明显：房价峰值区域位于一环的中西部，房价呈现自中心向四周逐渐降低的趋势，同时存在一定的空间变异性，房价分布不连续。天府广场作为成都市的市中心，房价的最高值却不在这一带，说明在成都市这样的大城市，传统的商务中心可能已经不再被认为是居住条件最好的区域。由于历史遗留原因以及后期的经济发展不均衡，造成成都市二手房价格整体分布趋势表现为南高北低、西高东低的区域特征。

对住宅价格的时空分布特征进行研究，给城市的规划和发展提供了良好的理论指导和实例验证，对未来城市和房地产市场的健康发展都具有一定的意义。