细长轴正反车削变形研究*

李 毅，胡晓兵，李现春，李彦儒

(四川大学 制造科学与工程学院，成都 610065)

0 引言

细长轴是一种长径比大于20的零件，由于其自身刚性较差，在车削过程中受到切削力、自身重力、切削热的作用容易弯曲变形，加工后的杆件成腰鼓形，竹节形，麻花形等使加工精度出现严重偏差，属于难加工类型工件。国内外很多学者在这方面作了研究。李方军等[1]采用专用夹具，对刀具材料，刀具参数，切削用量，进行详细分析和优化。沈志平等[2]采用“一夹一拉”的装夹方式加工细长轴，取得了理想的成果。邓志平等[3]建立双刀车削模型，并进行仿真模拟，确认了双刀车削的可行性。黄小东等[4]设计了一种双头带锥度车削专用机床，解决了细长轴加工过程中对心不准，振动较大表面质量较差的问题。叶建友[5]设计了一种射流支撑的细长轴加工方法，并通过实验验证了其可行性。以上几位学者的研究成果都是需要在特定的机床上加装特定的机构才能够提高细长轴的加工精度，如此造成成本升高且只适用于小批量生产。本文从工艺路线的角度出发，在普通的机床上不增加任何机构的情况下，探索在车削加工中正向走刀和反向走刀的差异，运用理论计算和ANSYS有限元分析对比分析两种走刀方式的结果，寻求最优的方法提高加工精度。

1 装夹方式的选择

生产加工中，工件的装夹是至关重要的，它是保证加工质量的前提和基础，尤其是加工细长轴这类刚性较差，对心较难，精度要求高的零部件，因此选择一个合适的装夹方式尤为重要。

细长轴常用的几种装夹方式主要有：一夹一拉，一夹一顶，两顶尖装夹。这三种方式各有优缺点，结合国内外学者研究成果以及现有的实验条件，最终选择了一夹一顶的装夹方法，其优点是安全可靠，对心较好，能够承受较大的轴向切削力，由于一端是顶尖，因此在受到切削热和轴向力时不会导致额外的弯曲变形。可将这种装夹简化为：卡盘装夹端为固定端，顶尖装夹为铰链支座，其简化如图1所示。

图1 装夹简化图

2 正向走刀的力学分析

2.1 力学模型

正向走刀时，细长轴受力分析如图2所示，车刀从铰链端(顶尖简化)向固定端(卡盘简化)做进给运动。其中：Fx为指向固定端的轴向力，Fy为径向力，L为总长，x为力的作用点距离固定端的距离，ys为径向力Fy和轴向力Fx共同作用下产生的位移。

图2 正向走刀受力分析图

2.2 分析计算

由材料力学[6]相关理论得到：

(1)

外圆车削时的切削力计算公式[6]：

Fy= 9.81×CFy×apxFy×fyFy×(60×v)nFy×KFyFx= 9.81×CFx×apxFx×fyFx×(60×v)nFx×KFx

(2)

式中，CFx，CFy决定于被切削金属和切削条件的系数；xFx，xFy为切削深度ap的指数；yFx，yFy为进给量f的指数；nFx，nFy为切削速度v的指数；KFy，KFx为修正系数。这些系数均可根据实际加工条件查询经验表得到。

3 反向走刀力学分析

3.1 力学模型

反向走刀时，细长轴受力如图3所示，车刀由固定端向铰链端做进给运动。

图3 反向走刀受力分析图

3.2 分析计算

由材料力学理论得到：

(3)

4 实例分析

根据某企业提供的材料，选择了如图4所示的活塞光杆进行理论分析。材料为结构钢，查表得到其弹性模量E=200GP,泊松比为0.3。总长为L=100mm，直径为d=4mm，其长径比达到了25，属于细长轴零件。

图4 活塞杆尺寸图

由于长径比较大，直径较小，参考一些文献和工程经验选择了下列切削参数：切削深度为ap=0.2mm，机床主轴转速为n=1500r/min，进给量为f=0.1mm/r。刀具选择硬质合金，根据上述切削参数，从机械设计手册中查表得，外圆纵车时：CFx取值为294，CFy取值为199；xFx取值为1.0，xFy取值为0.90；yFx取值为0.5，yFy取值为0.6，nFx取值为-0.4，nFy取-0.3。硬质合金刀具的主偏角为60°，前角为20°，修正系数KFx=0.777,KFx=0.539。

将模型简化，假定切削力在加工过程中保持不变，根据已知的参数可以计算出以下重要的参数：

(1)切削速度：

(4)

(2)径向力和进给力：

Fy= 9.81×CFy×apxFy×fyFy×(60×v)nFy×KFy=9.81×199×0.20.9×0.10.6×(60×0.314)-0.3×0.539=24.08N

Fx= 9.81×CFx×apxFx×fyFx×(60×v)nFx×KFx=9.81×294×0.21×0.10.5×(60×0.314)-0.4×0.777=43.79N

(5)

(3)转动惯量：

(6)

(4)其他参数：

(7)

4.1 理论计算分析

为了得到可靠准确的变形量数据，根据给定的材料，将活塞杆分为十段，每隔10mm取一个关键节点，根据变形量计算公式计算出每一个点的变形。见表1，得到了变形量与节点位置的计算数据。

为了更清楚显示其关系，如图5所示，运用Matlab强大的绘图能力在一张图上清楚地显示出两种走刀方式所得到的结果。

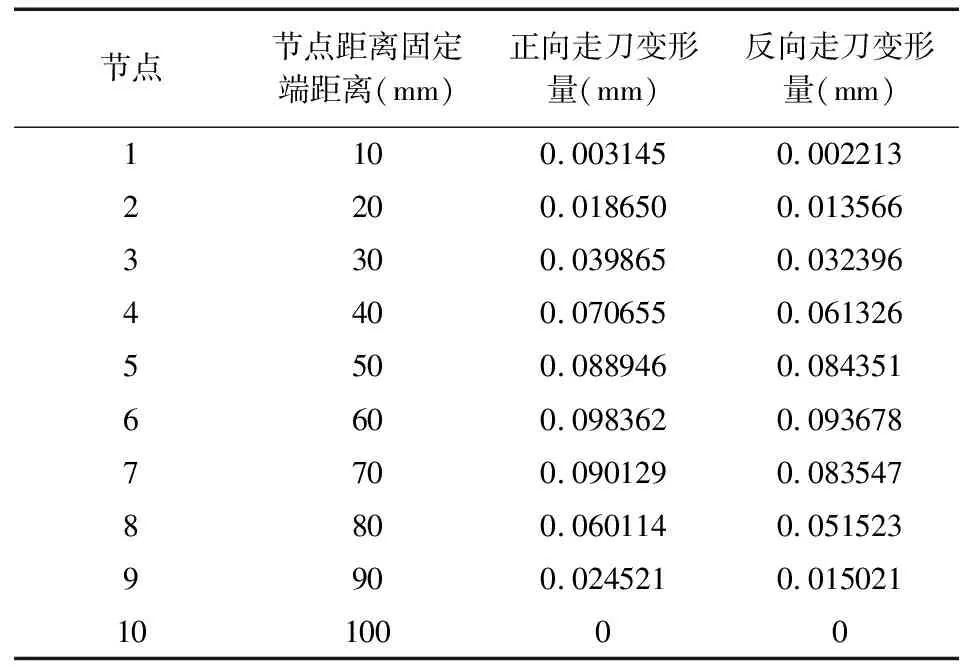
表1 理论分析数据

图5 数学模型计算变形曲线

从图上可以清楚看到无论正向走刀还是反向走刀，活塞杆的变形都是呈山峰状，在中间位置支撑较小的地方变形量大，两端变形量小，并且反向走刀变形量曲线始终在正向走刀变形量曲线下方。

4.2 有限元分析

为了进一步验证计算数据的可靠性，将采用ANSYS有限元分析软件对结构钢活塞杆的加工过程进行仿真分析。

为了更加接近真实的加工条件，对模型进行了如图6所示的载荷和约束的添加。对活塞杆左端施加固定约束B，对右端施加位移约束A(约束Y和Z两个自由度)，给整个工件施加一个转速为1500rpm的惯性载荷C，在关键节点位置分别添加Y方向偏置位移为-1.8mm(切削深度为0.2mm)的轴向力D(43.79N)和径向力E(24.08N)。

图6 载荷约束

经过ANSYS计算和后置处理得到表2所示数据。

由表2可知，正向走刀位于节点6时，ANSYS分析得到变形量最大值，与实际情况相符。图7所示该节点处的变形图。图8为此时工件的整体变形情况。

表2 ANSYS分析数据

图7 关键节点6变形图

图8 整体变形图

将所得数据绘制成如图9所示的坐标曲线图。

图9 ANSYS分析变形曲线

从图中可以看出，ANSYS所求解出来的变形曲线呈山峰状，两端小中间大，并且反向走刀的变形曲线始终在正向走刀变形曲线之下，这与本文通过数学模型所计算出来的结果吻合，因此证明数学模型可靠。在以后的生产加工中，可以在前期依靠理论计算所得数据，预测工件的变形状况，并在数控程序中进行实时补偿，减少加工前的试切工作量。

4.3 工艺结果对比

通过数据表和坐标曲线，可以清楚看出，在细长轴加工中，反向走刀比正向走刀加工精度更高。为了获得更具体的高精度数据，对数据进行筛选，由坐标曲线图可知，细长轴加工过中，两端的变形量很小，相对于中间部位可以忽略，因此取变形量较大的中间几个节点进行对比，结果如表3所示。

表3 提升精度

由表3可知，反向走刀的变形量比正向走刀小，加工出来的精度会比正向走刀高，通过数据的估算大约可以提高9.2%。

5 结束语

先通过选择合适的装夹方式建立理论计算和有限元分析的框架，经过数学模型的计算，得到细长轴两种走刀方式的变形曲线，再运用ANSYS对每一个点位进行静力学分析，同样得到两种走刀方式的变形曲线，综合分析发现有限元分析与理论计算的结果是一致的，反向走刀的变形相对正向走刀有所降低，在细长轴加工中反向走刀是一种更好的选择。