巧用定义解圆锥曲线客观题

江西省金溪县第一中学 郑蔚文

圆锥曲线的定义揭示了它们各自存在的条件、基本性质及几何特征。椭圆、抛物线、双曲线的定义既有相异的一面（第一定义），又有相同的一面（第二定义），定义就成了了解和研究圆锥曲线最重要的工具，下面不妨举例说明。

例1 动点P为椭圆上运动，且保持AB∥x轴，则△AMB的周长l的取值范围是（ ）。上异于顶点（±a，0）的一点，F1、F2为椭圆的左、右焦点，动圆I与线段F1P、F1F2的延长线及线段PF2相切，则圆心I的轨迹为除去坐标轴上的点是（ ）。

A.抛物线 B.一条直线 C.双曲线右支 D.椭圆

例2 已知点M（1，0），动点A，B分别在图2中抛物线y2=4x及椭圆的实线部分

图1

图2

分析：易知点M为抛物线和椭圆的公共焦点，设A（x1，y1）、B（x2，y2），则根据椭圆和抛物线的定义可得|BM|=|AM|=x+1，1又|AB|=x2－x1，所以解＜4，选C。

例3 如图3，已知抛物线x2=4y上的动点P在x轴上的射影为M，点A（3，2），则|PA|+|PM|的最小值为____________。

分析：延长PM交抛物线准线y=－1于点N，由抛物线定义知 |PN|=|PF|，则 |PA|+|PM|=|PA|+|PN|－ 1=|PA|+|PF|－ 1，要使|PA|+|PF|取最小值，点F、P、A三点必共线，此时|PA|+|PM|的最小值为|AF|－1=

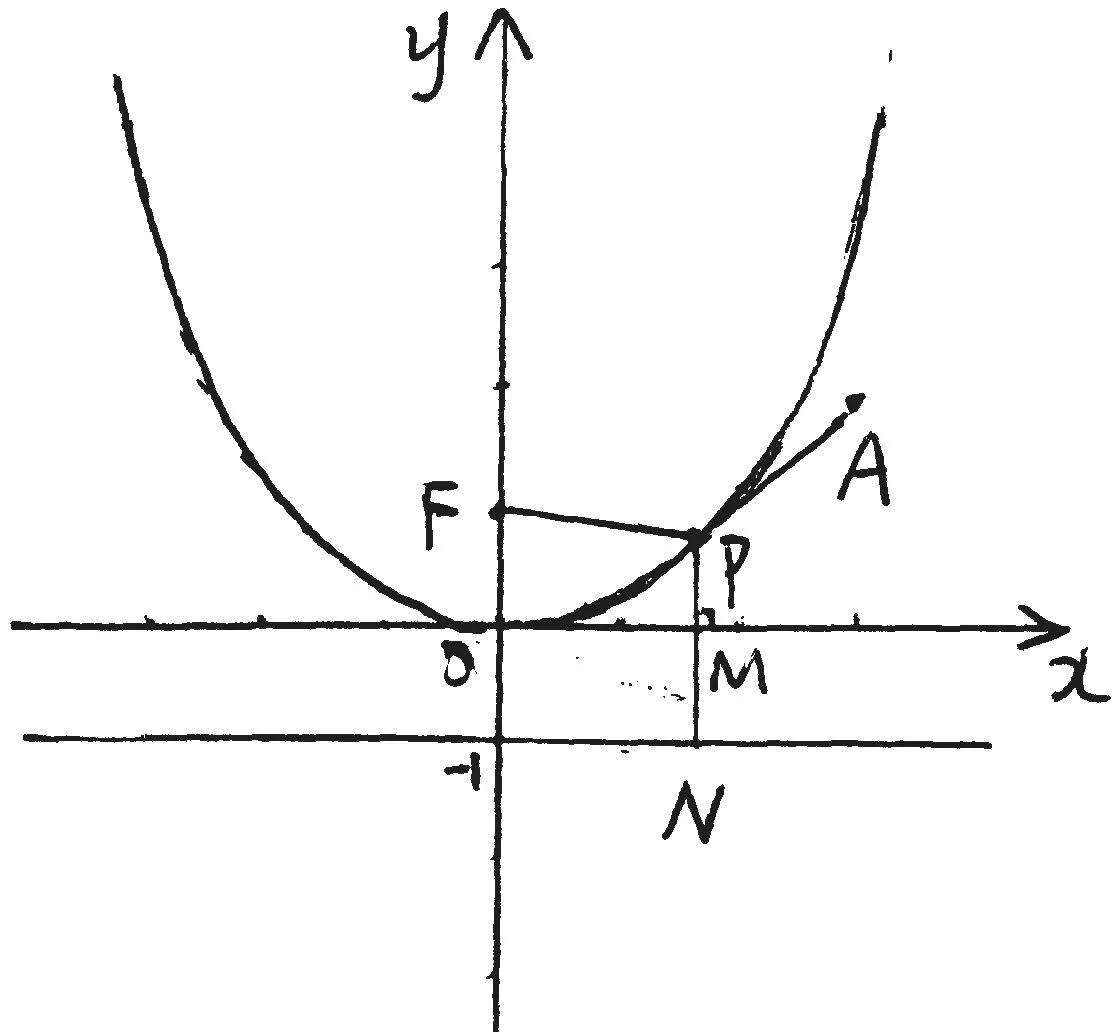
图3

例4 已知抛物线y2=4x，直线l的方程为x-y+4=0，在抛物线上有一动点P，P到y轴的距离为d1，P到直线l的距离为d2，则d1+d2的最小值为（ ）。

分析：如图4，设PM⊥y轴于M点，延长PM交抛物线准线x=－1于N点，根据抛物线的定义有|PN|=|PF|， 所 以d1+d2=|PF|+d2－1。 而 要|PF|+d2的值最小，只需过F作FH⊥l于点H，那么最小值为|FH|=选D也就很自然了。

例5 已知定点F1（－2，0）、F2（2，0），N是圆O：x2+y2=1上任意一点，点F1关于点N的对称点为M，线段F1M的中垂线与直线F2M相交于点P，则点P的轨迹是（ ）

A.椭圆 B.双曲线 C.抛物线 D.圆

分析：如图5，当N取圆O的右半侧时，因为直线NP为线段F1M的中垂线，所以|PF1|=|PM|，则 |PF1|－ |PF2|=|PM|－ |PF2|=|MF2|。连接ON，则ON为△MF1F2的中位线，所以|MF2|=2|ON|=2，即|PF1|－|PF2|=2。同理，当N取圆O的左半侧时，有|PF2|－|PF1|=2，由双曲线的定义知选B。

图4

图5

A.|OB|=e|OA| B.|OA|=e|OB|

C.|OB|=|OA| D.|OA|与|OB|关系不确定

分析：如图6，设△PF1F2的内切圆I分别与 边 PF2、PF1切于 点 C、D，延 长 F2B交 PF1于点E。由双曲线定义可知|PF1|-|PF2|=2a，又所以|PF1|-|PF2|=|F1A|-|F2A|=2a，显然点A为双曲线的右顶点。又因为F2B⊥PI且PI为∠F1PF2的平分线，所以点B为F2E的中点，这样，OB为△EF1F2的中位线，即两次使用双曲线的定义，可知|OA|=|OB|=a，选C。

图6

因此，在求解圆锥曲线，特别是涉及焦点、焦半径或准线等内容时，使用定义求解，往往能避免烦琐的推理与运算，进而快速、准确地解决问题。