梁变形特殊求解方法综述

宋 江 马亮亮

（重庆大学， 重庆 401331）

梁是土木工程结构中的一个重要构件，梁承受着多种形式的荷载，于是，对梁的研究就很有必要。目前，研究梁的变形的方法主要有积分法和叠加法，这是广大结构工程师最熟悉的方法，这两种方法的应用非常广泛。除此之外，研究人员根据理论分析和试验检验，也提出了其他的解决梁变形的方法。这些方法主要有：传递矩阵法[1]，能量法[2]，等效刚度法[3]，奇异函数法[4]，曲线拟合法[5]，悬臂梁法[6]。这些方法都有各自的优缺点，本文将主要介绍这些求解梁变形的特殊方法的原理以及算例分析。此外，随着计算机技术的不断发展，计算机技术已经渗透到各个学科之中，土木工程也不例外。因此，本文还将就计算机技术在梁变形中的应用提出展望，以期能丰富梁变形方面的研究。

1 梁变形特殊求解方法

目前，研究梁变形的方法主要有两种，即叠加法和积分法，这两种方法应用很广泛，然而，许多学者也提出了其他的关于梁变形的求解方法，下面，本文将依次介绍传递矩阵法，能量法，等效刚度法，曲线拟合法以及悬臂梁法这五种求解梁变形的方法。

1.1 传递矩阵法

1.1.1. 传递矩阵法的基本原理

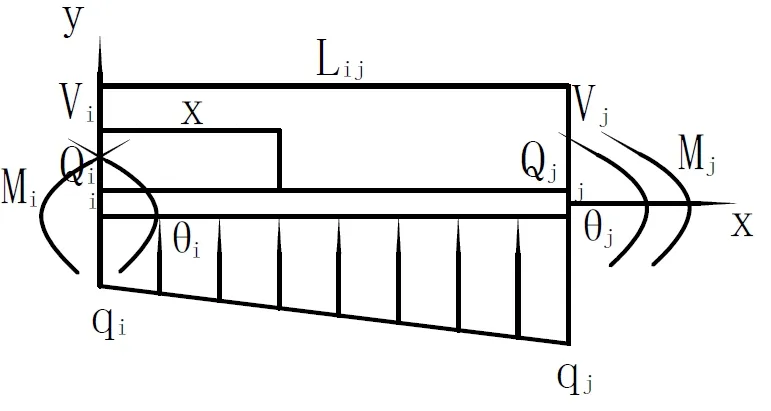
图1 任意段等截面梁

在多段梁中，取任意的 ij段等截面梁，其抗弯刚度为EI，如图1所示，其中 i端的位移分量为 Vi和iθ，内力分量为Mi和iQ,载荷集度为 qi； j端的位移分量为 Vj和 jθ,内力分量为Mj和Qj,载荷集度为 qj,分布载荷在梁段内为线性分布。各量的正、负号规定与通常的规定相同,图中所示的均为正。梁段内的弯矩方程[7]为:

在线弹性小变形的情况下，有：

如果梁段内没有分布荷载，（8）式可写为：

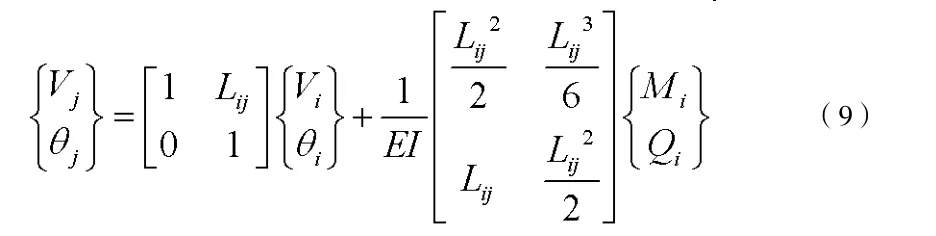
1.2 能量法

在工程结构分析中经常需要计算结构和构件的变形。使用一般的方法进行变形计算时，需要分析结构和构件的具体变形形式，计算量非常大。因此工程上通常采用能量原理完成结构和构件的变形分析。本文主要讨论的是莫尔定理，又称为单位荷载法。

1.1.2. 莫尔定理的推证

以下通过应变能概念推导莫尔定理。为了简化推证过程，以简支梁弯曲变形为例说明莫尔积分的基本概念。然后根据功能原理，推广到任意的杆系结构。

假设简支梁在任意荷载作用下，如图 3 所示，其弯矩方程为 M( x)，应变能为

式（14）为莫尔定理（Mohr’s theorem）的表达式.由于施加了广义单位力，故又称为单位力

法（Unit-load method）.

对于组合变形杆件，略去剪力对变形的影响，莫尔定理的一般表达式为：

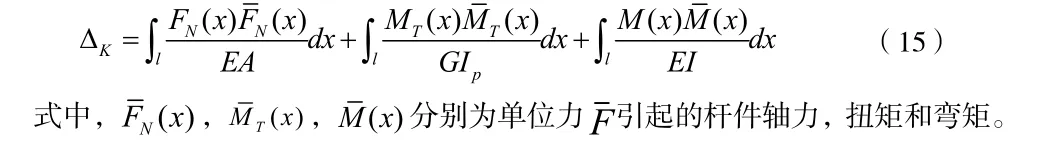
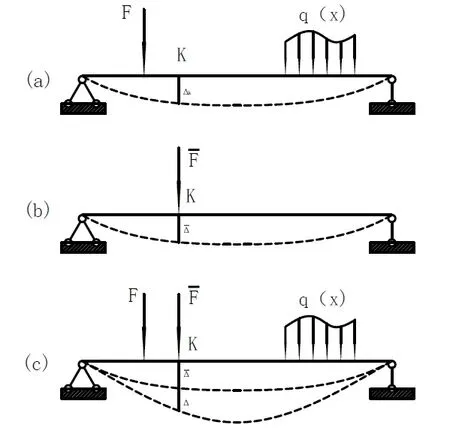
图2 任意荷载作用下的简支梁

1.3 曲线拟合法

本节从数学的角度出发,采用光滑曲线对梁的挠曲线进行拟合,根据梁上载荷作用面及支座处挠度各阶导数的物理性质和边界条件、连续条件求出拟合曲线的系数,从而得到挠曲线的数学方程。计算过程中不必写出梁的弯矩方程,且可以直接求解超静定梁的变形。

1.1.3. 曲线拟合法的基本原理

梁的挠曲线是一条光滑曲线，由积分法可知，在均布载荷作用下，挠曲线为四次曲线；在集中载荷作用下为

1.4 悬臂梁法

展望

本文所有的方法都是基于简单梁进行综述的，对于结构复杂，受力复杂的梁，仅仅依赖材料力学和理论力学的基本知识已经无法解决。当前计算机技术飞速发展，已经融入了各行各业，土木工程也不例外，计算机技术与土木工程的结合促使了有限元方法的巨大进步。对于复杂的梁的研究基本上都是基于有限元方法的。曾森等利用位移矢量插值法对空间曲梁的大变形进行了有限元分析[8]。朱宝田等利用空间扭曲梁有限元方法对汽轮机长叶片的动力和静力特性进行了研究[9]。

陶荣杰等对连续墙梁进行了有限元分析并且提出了简化计算的方法[10]。

宋子威等对铁路通用的B型梁进行了有限元分析，计算了自重和中-活载作用及荷载组合下的位移和应力、梁体的自振特性【11】。Rogério Carrazedo等讨论了层压板和壳体的有限元解决方案【12】。以上的学者补充了对各种复杂梁的有限元分析研究，未来，随着有限元的进一步发展，可以期望新的梁的有限元研究成果会越来越多。