基于椭圆曲线的识别伪基站垃圾短信改进算法
2018-07-25孙旭敏刘彩霞
孙旭敏,刘彩霞
(内蒙古大学 计算机学院,内蒙古 呼和浩特 010021)
1 概 述
1.1 伪基站
伪基站系统之所以能对用户发起进攻,是利用CSM网络单向鉴权的缺陷,即网络对用户的认证,用户终端对网络不进行鉴权以及空口信令完整性保护功能。GSM基站在与用户终端通信的过程中,终端无法检测网络身份是否合法,也无法判断接受到的网络信令是否来自合法基站。当手机终端接收到网络发送的标准信令,就会进行响应以及处理。利用这一缺陷,伪基站通过发出强于正常基站的信号,从而诱导移动用户手机的链接接入伪基站,获取覆盖范围内终端的手机串号IMSI/IMEI和电话号码,之后模拟任意号码向覆盖用户下发垃圾短信。在此期间,不仅手机会被强制接收垃圾短信,还会造成正常通信的阻断,伪基站覆盖区域内会出现大量掉话以及跨区频繁切换现象。
1.2 伪基站系统组成
伪基站系统主要是由信号处理子系统(伪基站和终端信号处理子系统)、用户操作平台和系统总控单元、天线和电源等部分组成,如图1所示。终端信号处理子系统用来实现对目标所在区域移动系统无线参数的侦查。系统总控单元完成对各子系统的控制与调度、信令处理、内部通信等功能。用户操作平台提供人机界面,能够进行系统状态的显示,小区状态的显示,目标数据库的存储、系统维护等功能。
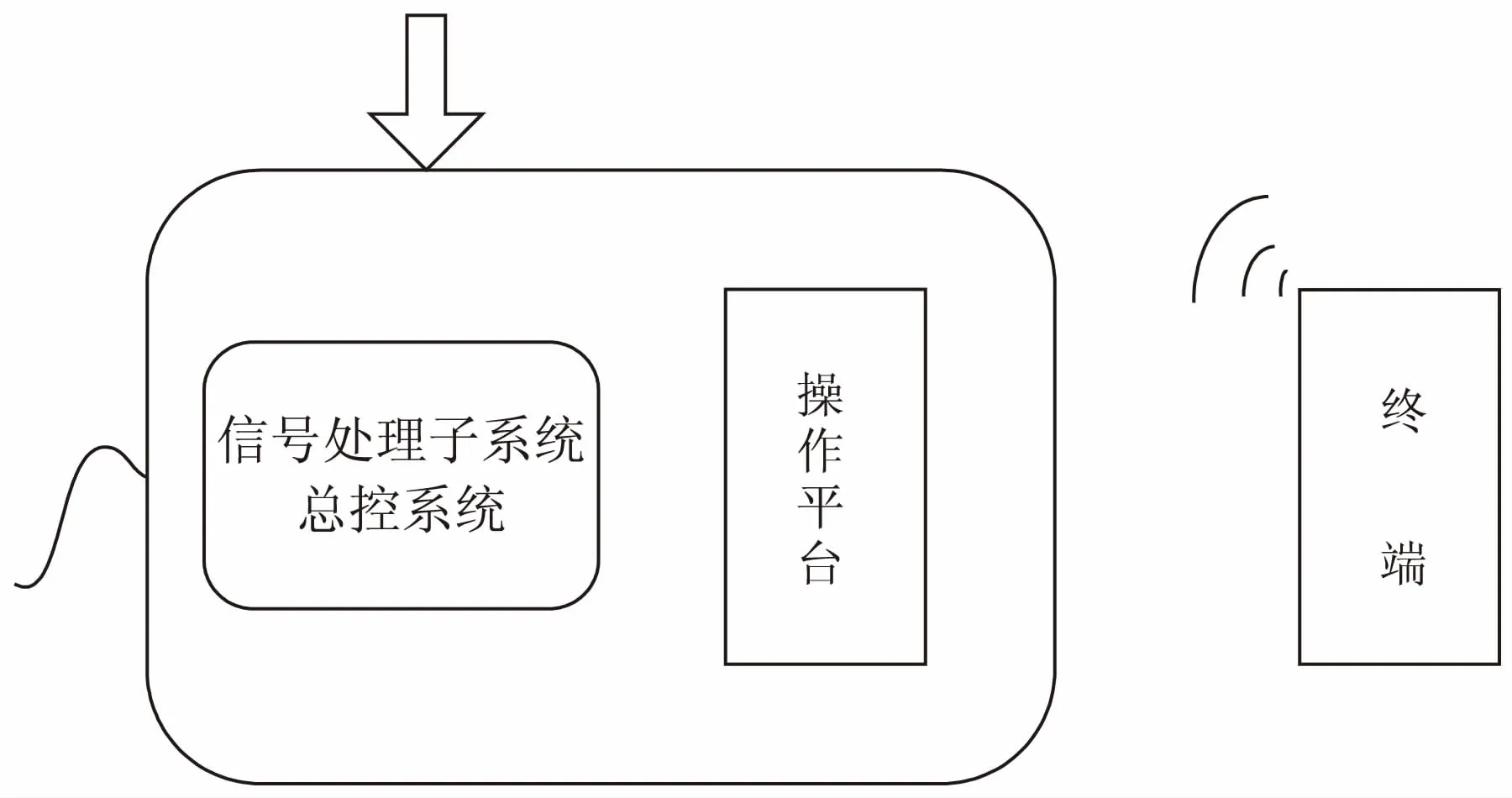
图1 伪基站系统结构
2 伪基站的系统原理
2.1 强制接入原理
目前的GSM采用单向鉴权机制,伪基站利用移动通信网络这一漏洞,仿冒运营商移动网络发射射频信号。伪基站的BCCH、功率参数与现网相同,LAC、CID与现网不同。由于伪基站设置的LAC与用户当前网络的LAC值不同,移动终端会认为所在位置发生变化,然后基于C2=C1+CRO(C1为手机接收信号电平值)优先选择C2值最大的信号快速重选到伪基站小区进行位置更新[1]。
移动终端向伪基站发送位置更新请求,伪基站借机通过MSC和BSC的信令模拟,获取目标手机IMSI、IMEI串号以及手机号码,直接向用户下发位置更新接收消息,确认位置更新后向终端下发垃圾短信[2]。此后伪基站为了避免因长时间驻留引起用户觉察,自动变换LAC,移动终端再次发起位置更新请求后,伪基站会根据数据库存储信息将已下发垃圾短信的手机剔除,发回拒绝消息“Location update rejected”,终端手机脱网,回到运营商网络。期间10~20 s,终端用户无法正常被叫,因手机被伪基站剔除后需要重新寻找网络,一般需要15 s左右才能重新驻留到GSM网络[3]。
伪基站工作原理示意图如图2所示。
2.2 下发短信机制
在GSM机制中,短消息的发送要经由移动终端所在区域的短消息服务中心(SMSC)的存储和转发,经研究伪基站下发垃圾短信的流程中,并不会经过SMSC中转站[4]。基于此漏洞,可以在短消息转发的过程中进行有效的数字签名,在接收终端上进行数字签名认证,在此过程选择合适的数字签名算法,确保其较高的安全性[5]。

图2 伪基站工作原理示意图
3 数字签名
3.1 数字签名简介
随着电子商务与电子政务的发展,对快速安全的加密算法有了新的需求。基于椭圆曲线的密码系统就以其卓越的安全性引起了专家学者的关注。椭圆签名算法的安全强度主要依赖于所选择的椭圆曲线[6]。
与其他公钥密码(如RSA、DSA等)相比,椭圆曲线密码具有绝对的优势:高安全、存储空间少、处理速度快、占用带宽少、扩展性好。在伪基站发送诈骗短信的识别中,数字签名主要提供一个身份标识,证实终端接收的短消息来自运营商。
3.2 识别伪基站垃圾短信数字签名思路
基于上文提到的伪基站下发垃圾短信的机制,对其进行分析发现数字签名的思路。
当SMCS收到短消息后,对其内容进行Hash运算得到消息的摘要。然后,SMCS用自己的私钥对消息摘要进行加密,将数字签名的摘要和短消息一起发送给用户的终端设备[7]。
数字签名算法的签名过程如图3所示。

图3 数字签名算法的签名过程
终端设备将收到的短消息采用相同的算法进行运算,得到一个短消息的摘要,并同时用SMCS的公钥对数字签名解密得到另一个短消息摘要,将两个消息摘要进行对比,识别其是否合法。若得到的两个摘要完全吻合,则短消息为合法消息[8]。数字签名的演算过程如图4所示。

图4 数字签名的演算过程
3.3 基于椭圆算法的数字签名
ESDSA是椭圆曲线加密体制ECC中应用的数字签名算法。实验表明,在椭圆曲线加密算法中采用160 bit密钥和1 024 bit密钥的RSA算法的安全性相当。由于椭圆曲线的加密算法密钥短,并且所基于的有限域的运算位数少于传统的运算位数,其加密算法很容易在计算机软硬件上实现[9]。
在基本的二进制序列中,椭圆曲线的运算速度取决于点乘运算以及求逆运算。如果能缩短点乘运算中的序列长度,以及避免求逆运算,则算法速度就会提高。基于这种考虑,文中提出了快速点乘运算的改进的椭圆曲线算法。
3.3.1 点乘的基础算法
首先,将一些基本符号规定如下[10]:
有限域K=Fq,有限域K上的椭圆曲线E:y2+xy=x3+a4x2+a6,其中x,y,ai∈K。椭圆曲线的基点为G,G不可任意改变,G点的阶为n,辅助因子为h。曲线上的两个点P(x1,y1),Q(x2,y2),Q不是无穷点ok,-p(x1,y1+x1)表示P的逆元。
定义E上的加法运算:
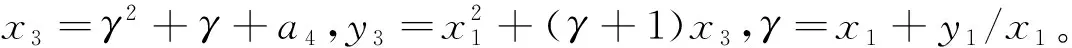
若Q≠P,且Q≠-P,Q+P=2p(x3,y3),其中x3=γ2+γ+x1+x2+a4,y3=γ(x1+x2)+x3+y1,γ=(y1+y2)/(x1+x2)。在有限域K上进行了3次乘法、1次求逆和9次加法。
设P为曲线E上的一个t阶点,且P∈E,0≤st且t∈N+。
S=an-1mn-1+an-2mn-2+…+a1m1+a0
(1)
其中,m≻1且0ajm,aj∈Z。
当m=2时,则有:
SP=(an-12n-1+an-22n-2+…+a121+a020)P=
an-12n-1P+an-22n-2P+…+a121P+a020P
(2)
由此可以看出要计算2iP,共需i次倍乘运算,且:
建立河道管理执法基地,加强河道管理装备建设和河道管理队伍能力建设。为加强河道管理装备建设,市水利局积极协调市财政局,将市级和区县级水行政主管部门归集的河道砂石资源费完全用于河道管理能力建设,购买河道巡查车辆,配置采砂在线监测系统、计算机、摄像照相等设备。各级河道管理站作为河道管理监督主管单位,要秉承服务至上的理念,努力为管理对象提供优质服务。一是提升协调能力,加强与相关单位的横向联系,建立定期沟通制度,主动为服务对象排忧解难。二是加强培训和考察,拓宽河道管理人员的知识面,提高应对复杂问题的处置能力,培养一批综合型人才,促进河道管理人员的结构优化。
(3)
基础算法需要在有限域K上进行7(n-1)次乘法以及2(n-1)次求逆[11]。
3.3.2 点乘的改进算法
由上述基本算法可知,SP的运算速度取决于n的大小,若选取适当的n=kN,其中N∈N+。令M=2K(K≻1),有:
S=an-1(2K)n-1+an-2(2K)n-2+…+a1(2K)1+a0
(4)
SP=(an-1(2K)n-1+an-2(2K)n-2+…+a1(2K)1+a0(2K)0)P=2K(2K…(2K(OK+an-1P)+an-2P)…+a1P)+a0P=2(2…(2(OK+an-1P)+an-2P)…+a1P)+a0P
(5)
改进的椭圆曲线算法如下:
Step1:
T[0]=OK
fori=1 to 2K-1
T[i]=T[i-1]+p
Step2:
T=OK
fori=N-1 to 0 by-1
begin
forh=1 tok
T=2T
forj=1 to 2K-1
ifj=a[i]thenT=T+T[j]
end
在Step1中共需要进行(2K-1)次加法运算,即需要做3(2K-1)次乘法和(2K-1)次求逆运算[12];在Step2需要进行N次点的加法运算和K×N次倍点运算,即需要做(3+4k)N次乘法运算和(k+1)N次求逆运算[13]。
基础算法与改进算法在倍点运算上区别不大,比较结果见表1。

表1 两种算法的运算步数
然而,在加法运算上面,当k与n满足n=2xk2ln2时,可使得算法效果达到最佳。
下面给出实例,随机取3个大整数进行计算,结果见表2。

表2 大整数的计算
由此可以看出,改进算法的有效性比基础算法提高了60%,考虑到短消息转发中心消息转发的及时性对用户的影响,改进的数字签名有助于加快签名和验证速度,能有效解决这一问题[14]。
4 结束语
伪基站系统对运营商的影响巨大,会导致覆盖区域大量掉话以及跨区频繁出现,并且会导致网络拥塞。对此,提出了一种改进的基于椭圆曲线的数字签名方法,将其应用于伪基站垃圾短信识别,相对于其他防治伪基站的措施具有一定的优势。将数字签名应用于伪基站垃圾短信的识别[15],对运营商网络不需进行修改;改进的椭圆曲线数字签名方法较其他算法具有较高安全性,且考虑到短消息转发中心要处理庞大的数据,改进算法的计算速度有所提高,而占用存储空间较小,便于在移动终端实现。
