河谷宽高比对高心墙坝黏土垫层剪切强度的影响

全锡志，陈鸿杰，黄文雄

(1.河海大学 力学与材料学院，江苏 南京 211100；2.华能澜沧江水电股份有限公司，云南 昆明 650214)

高心墙堆石坝常采用掺砾黏土作为防渗体,以增加心墙体刚度。水库蓄水后，心墙受自重应力及水荷载作用，在岸坡较陡或坡度发生变化时，心墙和堆石体与岩体坝基接触面常存在较大剪应力并产生较大的不均匀剪切错位变形[1-2]。黏土中的砾石容易因接触面处的剪切引起颗粒转动，并在坝基面邻近的黏土中产生孔穴，导致接触面处的渗漏。为了降低掺砾黏土心墙与坝基之间因直接接触剪切变形造成的接触面处渗漏风险，需要在掺砾黏土心墙与坝基之间设置纯黏土垫层。设计中有必要预先了解心墙与坝基接触面处的应力情况，确保黏土垫层的设置能达到预期目的。土石坝工程中，出现过接触垫层破坏的实例[3-4]。一般而言，接触面处的纯黏土垫层在满足强度条件情况下也能满足防渗要求。但当黏土垫层中或垫层与坝基接触面(界面)处应力达到或接近剪切强度极限时，接触面处的土体中会出现剪切带形式的应变局部化现象[5-6]。对于剪切带出现的情形下黏土垫层和界面处的渗透特性目前还缺乏充分的试验研究，但强度问题是黏土垫层设计中首要考虑的问题。

结合我国西南地区某水电站心墙堆石坝工程，应用有限元数值分析方法，研究心墙与坝基接触面处的应力情况和黏土垫层中的抗剪强度，重点在于考虑三维效应及河谷形状的影响。尽管文献中能见到对高心墙坝的应力分析[1,7-9]及河谷形状对坝体整体变形特性影响的讨论[10-11],但对于高心墙坝心墙与坝基接触面的应力计算和考虑河谷形状影响的黏土垫层强度分析尚不多见。因此，本文的计算和分析可为同类工程的黏土垫层设计提供参考。

1 有限元数值模型

1.1 工程概况

我国西南某水电站工程的掺砾黏土高心墙堆石坝，坝址处较狭窄的不对称“U”型河谷，河谷宽高比约为4.4，坝顶长576.68 m，坝顶宽12 m，最大坝高131.3 m，大坝上、下游坝坡均为1∶2；心墙最大高度127.8 m，心墙顶宽4 m，上、下游坡比1∶0.25；在掺砾黏土心墙与坝基接触面设置厚度2 m的纯黏土垫层过渡，坝基表面经过混凝土处理。

1.2 坝体简化和计算方案

为了便于对应力进行简单分析，本文对坝体几何形态进行了一定的简化[1，12]，主要是将河谷岸坡近似为平直。并且，尽管河谷和坝体具有不对称性，数值分析主要采用对称模型，通过改变岸坡角度考虑河谷不对称性的影响(参考图1和图 2)。模型坐标系定义为：X轴，顺河向，由上游指向下游，下游为正；Y轴，竖直向上，沿坝高延伸方向为正；Z轴，坝轴向，由坝中指向坝肩侧为正。

图1 堆石坝典型横剖面(单位：m)Fig.1 Typical cross-section of rockfill dam (unit: m)

图2 不同河谷宽高比计算方案示意(单位：m)Fig.2 Schematic diagram of calculation schemes with different width-height ratios (unit: m)

计算方案的主要几何参数如下：大坝高130 m，坝顶高程1 413.00 m，坝基高程为1 283.00 m，坝顶宽度12 m，上、下游坝坡约为1∶2；心墙顶宽3 m，上、下游坡比1∶0.25；三维模型的河床宽度均为126 m。坝体上游水库正常蓄水位为1 408.00 m，下游水位为1 328.00 m。

表1给出了不同计算方案对应的河谷宽高比，其中坝顶高程、上下游坝坡、筑坝材料以及填筑标准、坝体施工过程及水库蓄水情况均不变。作为对照，也对实际工程模型(不对称河谷)进行了三维计算(方案6)，此外还对坝体最大断面进行了平面应变计算(方案7)。

表1 有限元数值计算方案Tab.1 Computation cases for numerical analysis

1.3 数值模型

应用有限元商业软件ABAQUS对坝体进行数值分析。因主要关心坝体，特别是心墙与坝基接触面的应力情况，数值模型只包括靠近坝体的一小部分基岩。坝体材料采用目前工程界常用的邓肯-张E-B模型[13-15]，坝基材料采用线弹性模型。严格控制心墙与基岩接触面处的网格划分，尽量减小网格对结果的影响。二维堆石坝模型采用CPE4单元，单元数目为1 796个；三维模型单元类型均为C3D8，方案1～5的单元数目分别为10 994，10 480，9 985，9 468，8 676个，方案6为20 690个。

为了得到心墙与坝基接触面的应力分布，将数值模型简单区分为上游堆石区，掺砾黏土心墙，下游堆石区以及坝基(黏土垫层不参与计算)，坝体各分区材料参数取自实际工程三轴(CD)试验(见表2)，坝基材料参数:密度为2.45 g/cm3,弹性模量为1.5 GPa,泊松比为0.167。考虑坝体受力和变形的实际情况，二维模型将坝基底面以及两端设置X,Y方向约束；在三维模型中，位于对称面上的坝体和坝基设置为Z方向约束，坝基底面和侧面设置为X，Y，Z方向约束；坝体部分均不设约束。考虑到坝体施工分层碾压填筑(心墙与堆石体同步填筑)，荷载采用逐级施加的方式，计算按坝体施工填筑的先后次序分10级来模拟,每层13 m。蓄水阶段的模拟，考虑荷载的影响主要体现在两个方面，一是上游正常蓄水位以下的堆石体受到浮力作用；二是不透水心墙[16-17]受到上游库水压力、下游坝壳尾水压力的作用。

表2 主堆石料邓肯-张E-B模型参数Tab.2 Duncan-Chang E-B model parameters of main rockfill materials

2 接触面应力分布

2.1 心墙与坝基接触底面应力分布

心墙与坝基的接触面包括底面和侧面(岸坡面)，其中岸坡面上应力随河谷宽高比的变化具有一定复杂性[11]。图3和图4反映堆石坝蓄水后心墙底面顺河向剪应力和正应力沿坝轴线方向(参考图2)的分布情况(心墙底面坝轴向剪应力分量较小，未计入讨论)。总体而言，剪应力与正应力沿坝底轴线分布规律大体上一致：心墙底面中间5/6区域，剪应力和正应力分布较均匀，并且受河谷宽高比影响不大。心墙底面靠近岸坡脚的1/6区域，由于受岸坡对心墙变形的约束，剪应力和正应力显著减小。以方案3为例，剪应力减小幅值达66%，正应力减小26%左右。此外，河谷宽高比对这一区域的剪应力和正应力值都有一定影响。从强度角度分析，心墙底面中间的应力情况比较重要。

图5和图6所示为堆石坝蓄水后心墙底面顺河向剪应力和正应力大小沿河流方向的分布情况。从图中可以看出三维堆石坝几种计算方案之间的曲线走向基本一致。

从图5可知，心墙底面上游侧剪应力较大。这一现象表明心墙在上游侧水压作用下底面沿厚度方向的剪切变形不均匀，上游侧剪应变较大。心墙底面从迎水面向下游，在30 m范围内剪应力下降较快(降幅达36%)，30 m以后区段内剪应力变化不大。图6则表明，心墙底面上游侧的垂直正应力较小，体现了心墙偏心受压的结构受力特点，主要原因在于，上游坝壳堆石料浸水，受到浮力作用，故上游侧正应力值偏小[7-9]。从迎水面向下游20 m内，正应力增大较显著(增幅约13%)。其后正应力变化较小，约为1.85～1.91 MPa。下游坝壳不浸水，所以下游坝壳和心墙下游侧应力变化不大。

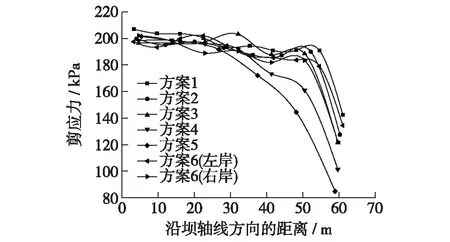
图3 心墙底面剪应力沿坝轴线的分布Fig.3 Distribution of axial shear stress at bottom of core wall

图4 心墙底面正应力沿坝轴线的分布Fig.4 Distribution of axial normal stress at bottom of core wall

图5 顺河向剪应力随距离的分布Fig.5 Distribution of downstream shear stress along with thickness of core wall

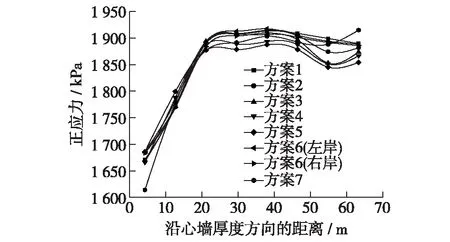
图6 顺河向正应力随距离的分布Fig.6 Distribution of downstream normal stress along with thickness of core wall

从图3～6中可以看出，几种三维计算方案得到的心墙底面沿对称轴应力分布曲线基本一致。与方案1相比，方案6(左岸)沿河流方向的剪应力偏小；与方案3比较，方案6(右岸)的剪应力在心墙底面中间区域偏大，靠近上下游部位偏小；方案6左岸部分心墙底面的正应力和方案1基本相同，右岸部分与方案3基本一致。与三维模型计算结果相比，按平面应变二维计算模型得到的底面剪应力值偏大，正应力值则差别不大。显然，三维模型能体现岸坡的作用，结果更为合理。

2.2 心墙与坝基接触侧面(岸坡面)应力分布

图7和图8分别反映了堆石坝蓄水后心墙与岸坡接触面中心线上岸坡向和顺河向剪应力分量大小随高程的变化情况。由图7可见，方案4在高程1 306 m位置附近(坝底向上约1/5坝高处)岸坡向剪应力值最大，约377.4 kPa，由于受到坝基约束，底部剪应力有所下降；从高程1 306 m到坝顶面这一区域，剪应力随河谷宽高比的减小而增大。方案6(左、右岸)分别与方案1、方案3比较，相应接触面上剪应力大致相同。图8中方案2在高程1 293 m位置附近剪应力值最大，约157.6 kPa；从高程1 360 m到坝顶区域，剪应力随着河谷宽高比(对称)的减小而增加。从建基面到高程1 350 m区域，方案6比方案1和方案3相应接触面上沿河流方向的剪应力分量要小，高程1 350 m附近以上大小基本相同。

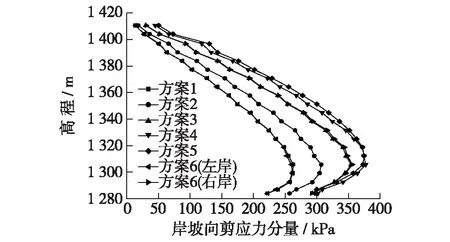
图7 岸坡向剪应力分量沿高程分布Fig.7 Distribution of slope-direction shear stress along with elevation

图8 顺河向剪应力分量沿高程分布Fig.8 Distribution of downstream shear stress along with elevation

对比图7和图8可见，在心墙与岸坡接触面上，沿岸坡和沿河流两个方向的剪应力分量大小分布随高程变化明显，大体上均先增后减；岸坡向剪应力分量值比河流向剪应力分量值大。

下面分析心墙侧面岸坡向和顺河向剪应力分量大小沿心墙厚度(河流方向)的分布情况。这里以方案4最大剪应力值的高程1 306 m位置为例进行讨论。

岸坡向剪应力分量大小沿心墙厚度变化不大。方案1～4计算结果受河谷宽高比影响较大，方案5结果比方案4略小，岸坡角在50°左右时，岸坡向剪应力最大(见图9)。方案6岸坡向剪应力分量，左岸计算结果与方案1相比偏小；右岸计算结果与方案3相比偏大。图10表明，河谷宽高比对顺河向剪应力分量大小有一定影响，最大剪应力随岸坡角增大而减小。剪应力从心墙迎水面侧向下游逐渐减小，最大值发生在心墙迎水面侧。

图9 1 306 m高程岸坡向剪应力分量沿心墙厚度的变化Fig.9 Distribution of slope-direction shear stress along with thickness of core wall (1 306 m)

图11和图12所示为心墙与岸坡接触面中心线上总剪应力和正应力随高程变化的情况。图12表明，从坝顶处向下，心墙与岸坡接触面上正应力大致接近于线性变化。最大正应力发生在略高于心墙底面的位置。在心墙侧底面附近，由于受坝基对变形的约束，正应力有所下降，呈非线性分布。从图13可以看出，总剪应力大小随高程的变化趋势与图9基本一致。总剪应力随河谷宽高比的减小而增大。总剪应力最大值大致发生在1/5坝高附近，岸坡较陡的情况下总剪应力最大值的位置有所上移。

方案1～4计算结果中，总剪应力随岸坡角增大而增大；方案1～5计算结果中，正应力随岸坡角增大而减小。非对称情形(方案6)计算结果分别与两种对称情形(方案1和方案3)计算结果相比较，左岸岸坡面中下部总剪应力偏小，中上部以及右岸差异不明显；正应力大体一致。

图11 心墙岸坡中心线上总剪应力随高程的分布Fig.11 Distribution of total shear stress along with elevation on centerline of bank slope

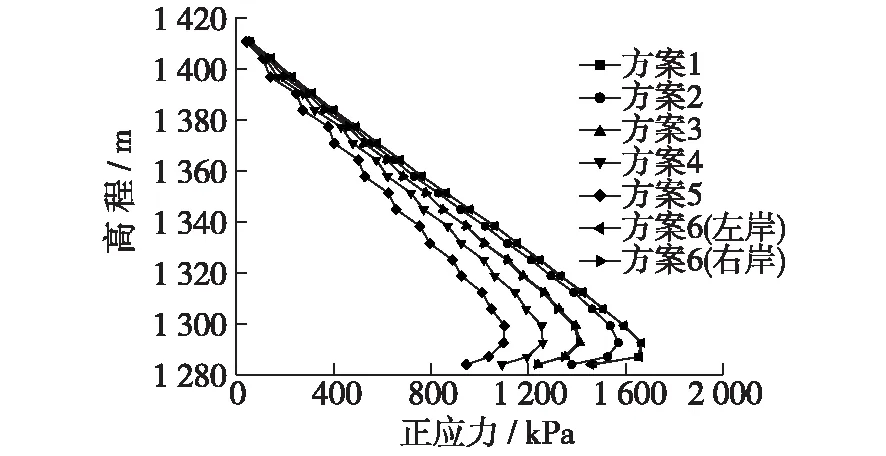
图12 心墙岸坡中心线上正应力随高程的分布Fig.12 Distribution of normal stress along with elevation on centerline of bank slope

图13和图14展示1 306 m高程总剪应力和正应力沿心墙厚度的分布规律。同样可以看出，心墙迎水坡面侧总剪应力较大而正应力较小。

图13 1 306 m高程总剪应力沿心墙厚度的分布Fig.13 Distribution of total shear stress along with thickness of core wall (1 306 m)

图14 1 306 m高程正应力沿心墙厚度的分布Fig.14 Distribution of normal stress along with thickness of core wall (1 306 m)

将方案1～5计算得出的心墙迎水坡面侧总剪应力值随岸坡角的变化点通过曲线拟合，可以看出，剪应力值在岸坡角为45°左右时最大(图15)。心墙与岸坡接触面处黏土垫层中土颗粒处于三向压应力状态，在接触面黏土颗粒一点 (单元体) 处，任意方向截面上应力所对应的点的坐标，必定位于图16所示3个应力圆所围成的阴影区域内，该点处的最大剪应力为A点的纵坐标，作用在与σ2主平面垂直，并与σ1和σ3所在的主平面成45°的截面上[18]。

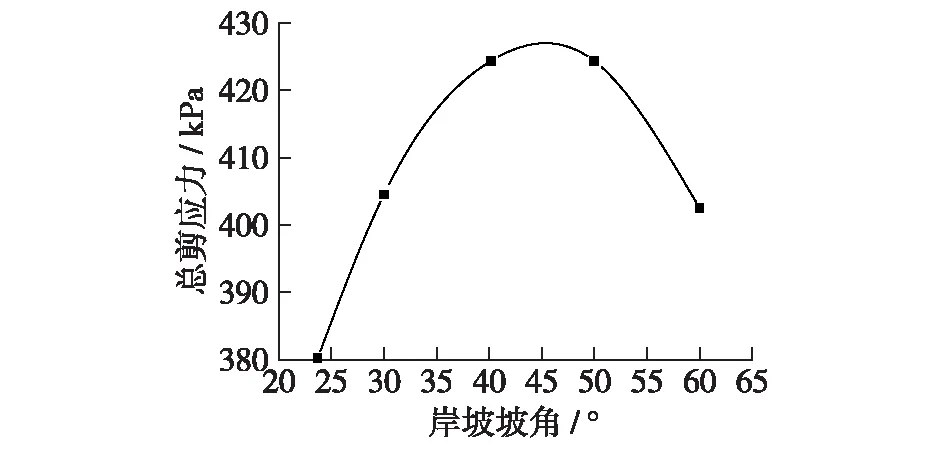
图15 总剪应力与岸坡坡角的关系Fig.15 Relationship between total shear stress and angle of slope

图16 三向应力状态应力圆Fig.16 Stress circle of three dimensional stress state

计算模型将河谷岸坡近似为平直坡面，土体有沿岸坡面滑动的趋势。李登华[19]在接触面试验过程中利用数字图像位移量测技术观测接触区土体变形以及土颗粒位移情况时，也证明了这一点。由于基岩的约束作用，黏土颗粒沿岸坡面滑动。当岸坡坡面与黏土单元体破坏面一致时，剪应力最大，所以黏土垫层剪应力最大值出现在岸坡坡角45°左右。

3 黏土垫层抗剪强度分析

通过数值模拟，得到了心墙与坝基接触面上的应力。基于此，本节对纯黏土垫层的抗剪能力按莫尔-库伦强度准则进行评估。为此定义抗剪强度系数R=τf/τN=(c+σNtanφ)/τN作为定量分析指标，其中τN和σN分别为心墙与坝基接触面上的工作剪应力和正应力；c和φ为黏土垫层的抗剪强度参数。

在接触面有黏土垫层的情况下，需要考虑两种可能的破坏情况：即黏土垫层内的剪切破坏或黏土垫层与坝基接触面处的剪切破坏。通常黏土垫层内的破坏以剪切带的形式出现，剪切带的厚度与土颗粒粒径相关[5]。若剪切破坏发生在接触面处，则剪切带出现在与坝基接触的黏土中,剪切带厚度还受到接触面粗糙度的影响[6，20]。实际工程的坝基经过混凝土处理，具有一定粗糙度。因此，无论是黏土垫层内剪切破坏还是黏土垫层与坝基接触面处的剪切破坏，均主要与黏土垫层的抗剪强度有关。已有的黏土直剪试验及黏土-混凝土接触面剪切试验成果[21]也证明了这一点, 即在结构面相对粗糙的试验条件下，试验得到的黏土垫层内剪切强度参数c和φ值均低于界面剪切破坏相应的强度参数值。因此这里的强度分析中，采用黏土垫层的强度参数即可。

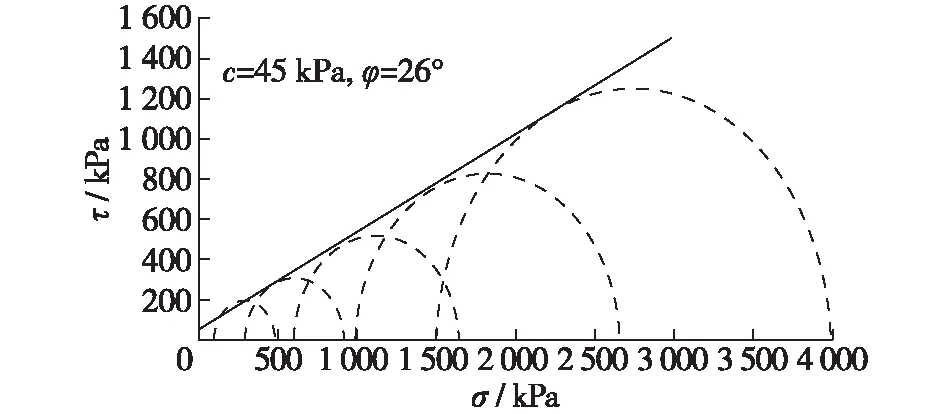
图17 黏土料排水三轴剪强度包络Fig.17 Drainage triaxial shear strength envelope of clay material

本项工程实例提供了黏土垫层的排水三轴剪试验数据。根据莫尔-库伦强度准则, 黏土的剪切破坏不受中主应力的影响。因此，可以按黏土垫层的排水三轴剪试验数据确定黏土的抗剪强度参数，参考图17，取强度参数c=45 kPa,φ=26°。

心墙与坝基接触底面正应力较大，剪应力相对较小，R值远大于1，一般不会发生剪切破坏。这里主要讨论心墙与坝基接触侧面(岸坡面)的抗剪强度。图18和19分别给出了心墙与岸坡面沿高程及中部沿河流向抗剪强度比R的变化规律。

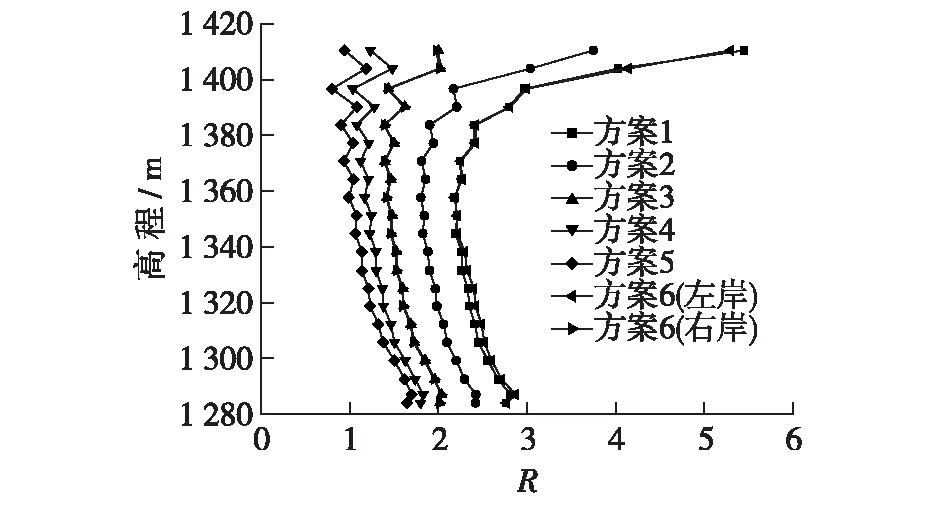
图18 R与高程之间的关系Fig.18 Relationship curves between R and elevation

图19 1 358 m高程R沿心墙厚度的分布Fig.19 Distribution of R along with thickness of core wall (1 358 m)

由图18和19可见，对于岸坡角较小的情形(方案1和2)，R最小值发生在岸坡中部偏上的位置，数值较1.0大得多，一般不会发生黏土垫层的剪切破坏。随着岸坡角增大，R值减小，最小值发生部位上移。计算方案4和5 (对应坡角大于45°)，对应的抗剪强度系数R值在岸坡上部区域小于1.0，表明心墙与岸坡上部的纯黏土垫层存在较大的剪切破坏风险。从图17可以看出，临界状态线拟合总体上很吻合，高应力区的c，φ值与工程实际偏差很小，低应力区c值偏小，φ值偏大。由于坝顶岸坡面垂直正应力过小，抗剪强度主要由c值控制，因此坝顶附近R值偏小，高估了心墙与岸坡上部纯黏土垫层的剪切破坏风险。

4 结 语

应用有限单元法对高心墙堆石坝心墙与坝基接触面处的应力进行计算，重点考虑不同河谷宽高比的影响，分析了黏土垫层的抗剪强度，据此总结出对实际工程有参考意义的规律。

(1) 河谷宽高比对心墙底面应力的影响不显著。心墙底面正应力较大，相应的抗剪安全性较高。纯黏土垫层的强度安全主要由岸坡面的应力所控制。

(2) 心墙与岸坡接触面上正应力与剪应力均为上部小、下部大。正应力沿高程大致为线性变化，在底部附近达峰值后有所下降；剪应力最大值出现在底部向上约1/5坝高处。

(3) 河谷宽高比对心墙与岸坡接触面上正应力与剪应力影响较显著。总体而言，正应力随岸坡角增大而减小，剪应力随岸坡角增大而先增后减；45°左右岸坡对应的接触面上剪应力最大。应采取措施防止(1/5坝高处)黏土垫层出现大剪切变形从而导致接触面发生渗漏破坏。

(4) 按莫尔-库伦强度准则分析，岸坡中上部的抗剪强度系数较小。岸坡角越大，发生黏土垫层剪切破坏的风险越高。在本文的工程实例中，若岸坡角大于45°，岸坡上部将发生黏土垫层剪切破坏。在岸坡坡角大于45°的狭窄河谷中修建高心墙堆石坝时，为防止心墙发生剪切破坏，建议心墙与岸坡接触面(特别是在上部)使用抗剪强度较高的黏土材料或者采取工程措施加强黏土的抗剪能力。

(5) 与对称模型相比，实际工程(非对称河谷)模型左岸岸坡中下部黏土垫层抗剪强度系数偏大，偏安全，中上部以及右岸抗剪强度系数相近。