压电陶瓷微位移的光干涉测量与控制系统

齐艳强，赵晓丹，李孟阳，张明达，b，陈智辉，b，杨毅彪，b

(太原理工大学 a.物理与光电工程学院，b.新型传感器与智能控制教育部重点实验室，太原 030024)

压电陶瓷致动器是近年来发展的高精度微位移致动器件,具有体积小、位移分辨率高、易于控制等优点，但也存在迟滞、蠕变等非线性特性[1-2]。而迟滞特性是压电陶瓷非线性产生的主要原因，对迟滞进行补偿并实现微小位移的高精度检测[3]是压电陶瓷精准控制的关键。

常用的微位移检测设备主要有电容测微仪[4-5]、电感测微仪[6-7]、激光干涉仪[8-9]等。电感测微仪和电容测微仪稳定性好、测量速度快、精度高，但容易引入外界干扰，且价格昂贵[10]。迈克尔逊干涉仪是一种应用非常广泛的激光干涉测量设备，但由于光学原理限制，测量精度只能达到λ/2.通过对迈克尔逊干涉法的进一步改进，引入干涉条纹细分[11]、电子倍频[12]等技术，可使测量精度达到λ/10.进一步完善测量技术，通过光学倍程方法[13-14]提高其测量精度是激光干涉位移测量技术的一大发展趋势。

本文针对压电陶瓷的非线性特性，提出一种高精度微位移检测与控制系统。针对迈克尔逊干涉仪测量精度不高的问题，通过引入具有位移放大功能的多次反射装置，以期实现位移测量精度的进一步提高。建立位移放大系数与光源入射角β、动镜与定镜夹角α之间关系的数学模型，并对光学系统进行仿真验证。通过建立压电陶瓷致动器的迟滞模型，以前馈控制方式实现压电陶瓷的精准定位。

1 迈克尔逊干涉的光路放大方案

迈克尔逊干涉技术是以激光波长作为基准，通过光的干涉原理对引起光程变化的微小位移进行测量的技术。传统的迈克尔逊干涉仪的原理如图1所示。

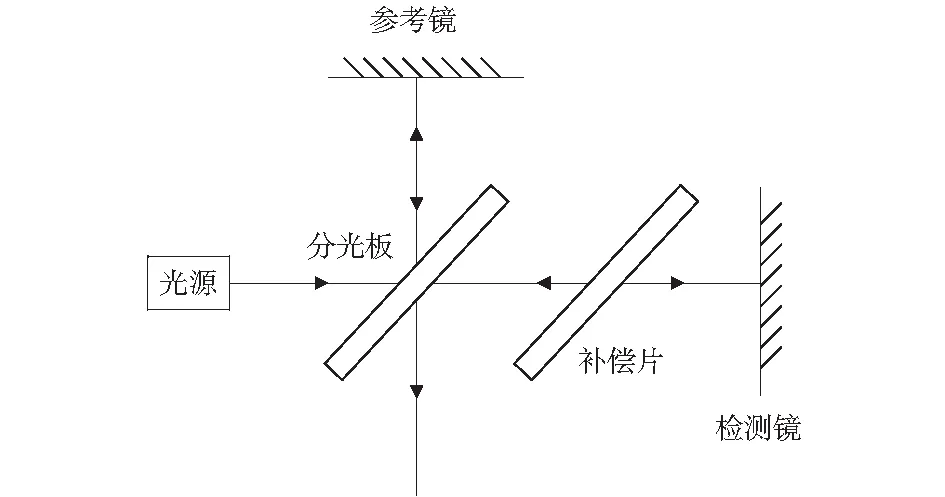
图1 迈克尔逊干涉原理Fig.1 Principle of Michelson interferometer

迈克尔逊干涉仪结构简单，应用广泛，但其分辨率只能达到λ/2，其亚微米级的测量精度无法满足压电陶瓷微小位移的测试与控制需求。本文在迈克尔逊干涉方法的基础上，利用多次反射原理，引入了光路放大装置，原理如图2所示。其中光程放大系统主要由两面高反射率的平面镜构成，动镜与定镜夹角为α.当光束以入射角β射入定镜时，如果β/α=N，入射光经过N次反射后垂直入射到动镜，再经过N次反射原路返回。将压电陶瓷垂直粘贴在动镜上，通过超高精密电动旋转台改变定镜与动镜的夹角α.当压电陶瓷受到电压驱动产生纳米级微小位移d时，该装置能够有效放大入射光线的光程。以该光路放大装置替代迈克尔逊干涉仪中的检测镜，具体光学系统如图3所示。

图2 光路放大装置原理图Fig.2 Principle of optical amplifier

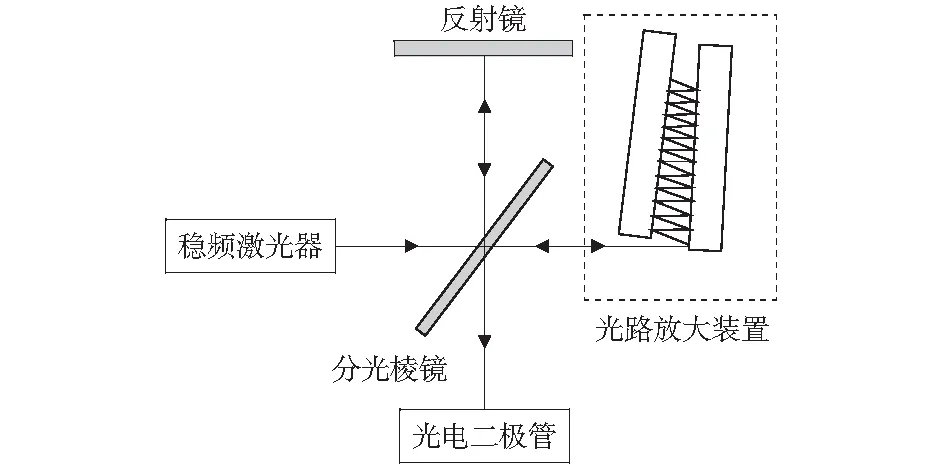
图3 基于光干涉的位移检测系统Fig.3 Displacement detection system based on optical interference

2 理论计算与仿真验证

每次反射造成的光程变化S(i)为：

(1)

式中：光路放大装置中压电陶瓷的位移为d；光源射入定镜的入射角β；动镜与定镜夹角α；i为每次反射的入射角.

因为多次反射过程中每次反射光程差的表达式相同，i每经过一次反射减小2α.则将每次反射的光程变化量相加，即可得到不同β和α下的光程变化量S与压电陶瓷位移d的倍数关系。具体如图4 所示。

为了使迈克尔逊干涉测量精度达到纳米量级，光路放大装置的放大倍数需要大于100.根据计算结果可知，在α=1°，β>45°或α=2°，β>74°或α=3°，β>81°的条件下理论上能够满足上述需求。进一步的提高放大倍数可通过增加入射角β或减小α来实现。

为验证理论计算结果的正确性，建立相应的光学仿真模型。设定光源为He-Ne激光器，波长λ为632.8 nm.初始设定动镜和定镜大小都为边长为40 mm的正方形，动镜到光源的距离L=125.000 μm，倾斜角16°，定镜距离光源139.000 μm，倾斜角14°.即系统处于α=2°，β=14°的情况下，通过仿真得到干涉图样如图5所示。

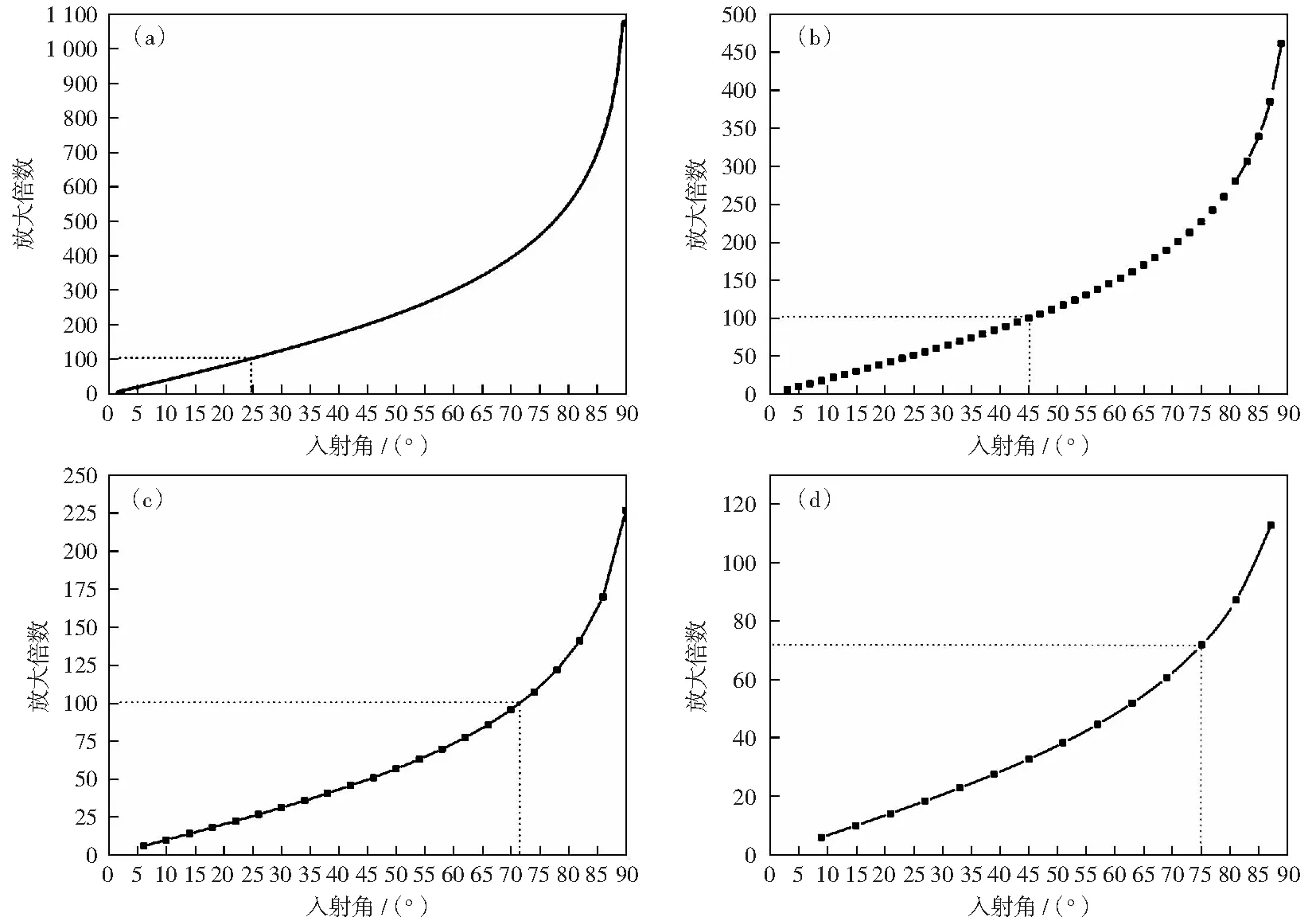
图4 不同β和α下的光路放大倍数(a) α=0.5,(b) α=1,(c) α=2,(d) α=3Fig.4 Optical amplification at different β and α

图5 干涉图样(β=14°，α=2°，L=125.000 μm)Fig.5 Interference pattern (β=14°，α=2°，L=125.000 μm)

根据理论计算结果可知，当α=2°，β=14°时，放大装置的放大倍数为14倍。光程变化半个光源波长所需动镜的变化量为：

(2)

即动镜到光源的距离L每变化0.164 μm，理论上干涉场中固定点处的明暗条纹变化一次。仿真模拟时分别设置L为125.164 μm，125.328 μm，125.492 μm，其对应干涉图样如图6所示。

图6 动镜位置变化后的干涉图样Fig.6 Interference pattern after changing the position of the moving mirror

由干涉图样可观测到，干涉场中固定点处的干涉条纹明暗变化一次，即动镜位移变化164 nm能够使光程差变化λ/2，系统的模拟结果与理论计算相符。

3 微位移测量与控制系统的建立

基于迈克尔逊干涉法，结合光路放大装置，搭建了光干涉测量与控制系统。致动器采用RP200堆叠型压电陶瓷，驱动电压0～150 V，标称位移1.8 μm.将定镜固定于旋转台上，通过RAUK超高精密型旋转台调节定镜与动镜的夹角以及光源入射的角度。采用PDA10A型硅基跨阻放大光电探测器将干涉光信号转换为电压信号。以基于FPGA的高速数据采集卡对光电探测器的输出电压信号进行采集。受限于本次实验数据采集卡的采样速率，位移放大装置的放大倍数不宜过大。实验设置α=2°，β=14°，放大倍数为14.压电陶瓷致动器每移动22.6 nm，光电探测器的输出电压变化一个周期。

以开环控制方式对压电陶瓷迟滞非线性进行补偿，首先需要建立压电陶瓷迟滞模型。对RP200堆叠型压电陶瓷施加幅值从0增加到150 V的直流电压，通过电感测微仪测量得到压电陶瓷的高精度的位移数据如图7所示。

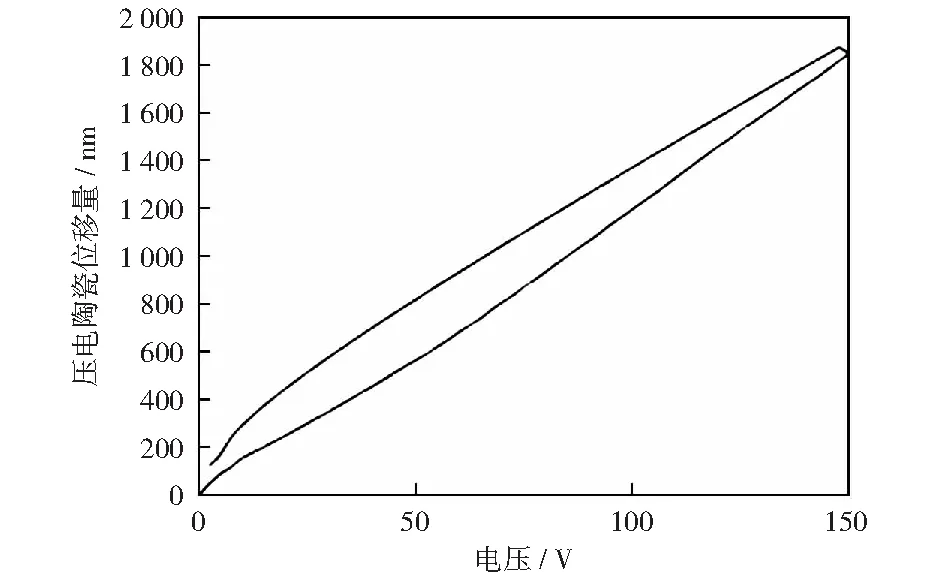
图7 压电陶瓷电压与位移关系Fig.7 Relationship between voltage and displacement of piezoelectric ceramics

根据测量结果，以极坐标方式对其迟滞特性进行数学建模，得到该压电陶瓷的迟滞特性方程：

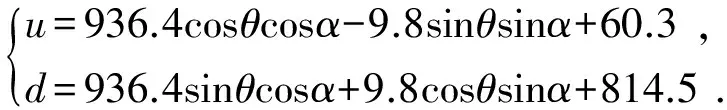
(3)

式中：θ=1.487 5，α为极坐标的角度。经拟合所得的压电陶瓷迟滞特性曲线如图8所示。

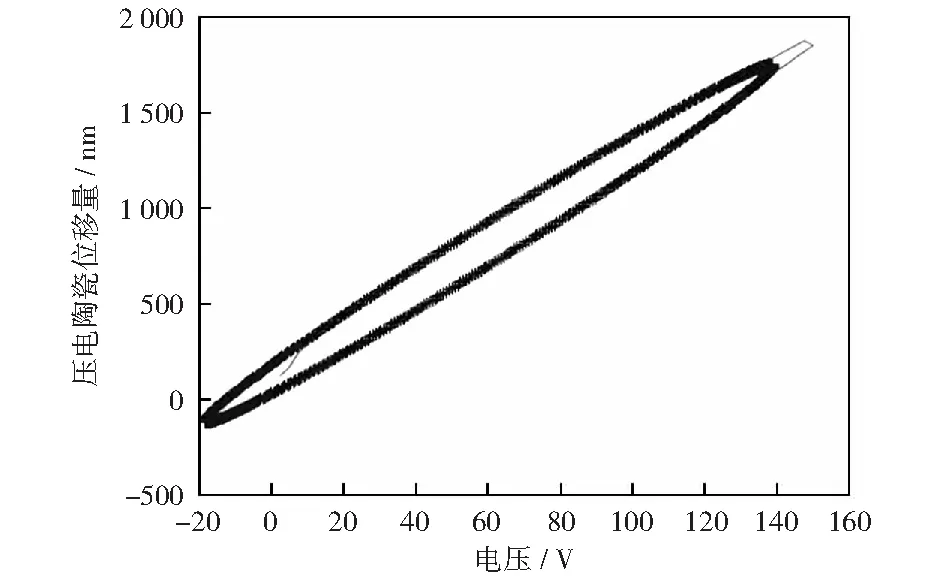
图8 拟合曲线Fig.8 Fitting curve

根据压电陶瓷的迟滞特性方程(3)，以22.6 nm为步长，代入到压电陶瓷迟滞逆模型方程得到其相应的一系列控制电压。将所得控制电压逐一施加于压电陶瓷，光电探测器将干涉条纹光强的变化转化为电压幅值的变化，通过对电压幅值变化周期数进行计数得到压电陶瓷的实时位移。具体实验结果如图9所示，其中散点为光干涉测量系统测得的位移数据，曲线为电感测微仪测得的高精度参考数据。

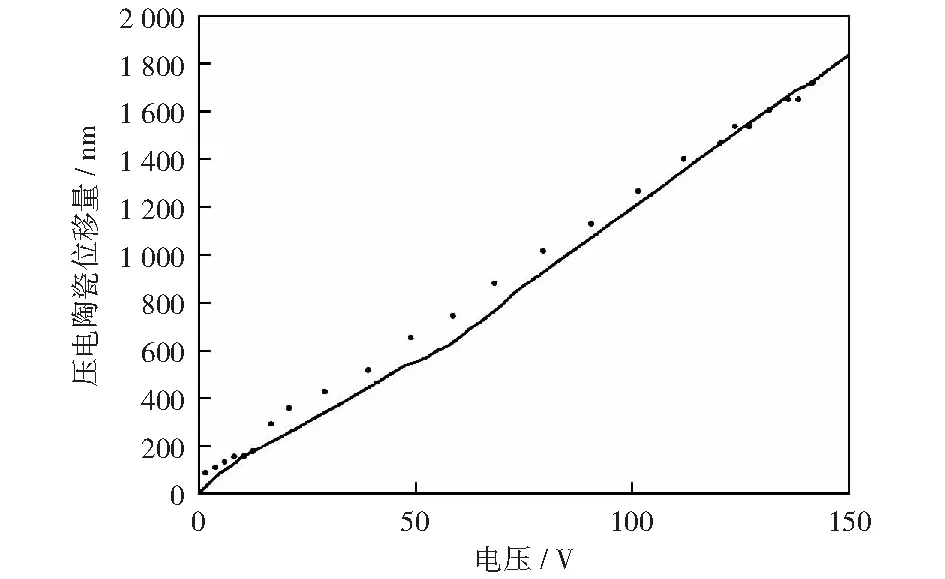
图9 测量位移误差Fig.9 Measuring displacement error

根据图9可知，该位移控制系统在压电陶瓷以低于10 V驱动时，其误差较小，可控制在一个步长即22.6 nm之内；当以10～90 V电压驱动时，误差逐渐增大，在49 V时达到了最高98 nm，达到了拟合曲线位移的7.2%；高于110 V驱动电压时，误差也降低到22.6 nm之内；在驱动电压高于120 V时，误差最小，可控制在10 nm之内。控制误差的均方差为46.6 nm，超过了两个步长。该控制方法在一定程度上能够补偿压电陶瓷的迟滞非线性，为了提高压电陶瓷定位精度可进一步结合闭环控制来实现。

4 结论

针对压电陶瓷的迟滞非线性，采用开环控制的方式对其进行补偿，以结合光程放大装置的光干涉测量系统对压电陶瓷的输出位移进行测量。通过理论计算与光学仿真验证了光程放大装置的放大作用：理论上可将迈克尔逊干涉法的测量分辨率提高到纳米量级。使用分辨率为22.6 nm的光干涉测量系统对压电陶瓷位移进行测量，结果表明：该测量与控制系统误差的均方差为46.6 nm，在小范围内可将控制误差减小到10 nm以下，在一定程度上可实现压电陶瓷的精准定位。