基于对偶模型的公司最优红利数值模拟
2018-07-21邓丽
邓 丽
(韶关学院 数学与统计学院,广东 韶关512005)
随着金融、保险、股东制度的盛行,公司的现金流优化问题也越发受到重视,即制定最优红利策略使得股东的期望收益值最大.如果公司只考虑股东的最优红利,就会加速公司破产;如果只考虑破产概率最小,就会使股东利益受损,挫伤其投资积极性,因此公司最优红利问题通常结合风险模型进行讨论.1957年De Finetti[1]讨论了离散经典风险模型的最优红利策略,从而提出了风险理论的分红问题.目前关于Barrier 策略[2-3]和 Threshold 策略[4-6]的讨论较多,也有学者讨论复合二项对偶模型的最优分红[7-8]和随机利率下相依索赔的离散风险模型的分红问题[9].本文讨论对偶模型下公司红利的最优分配方法,运用压缩映射理论和Berman递归算法在R软件中进行数值模拟,得出最优的红利策略是Threshold策略,数值模拟的结果说明结合风险模型讨论的公司最优红利更有意义.
1 最优值函数
讨论红利问题的对偶模型为:
其中c∈N+表示公司在时间区间(t-1,t]内的投资,S(t)表示公司直到时刻t的累积收益.
在考虑随机投资的复合二项模型中,假设任意(t-1,t]内最多有一次收入Xt(i.i.d.),其概率函数f(x)=Pr(Xt=x)用εtct=1(或0)表示在(t-1,t]内支出为Ct的条件下有一次收入(或没有收入),{εtct}(i.i.d.)与{Xt}相互独立,满足:
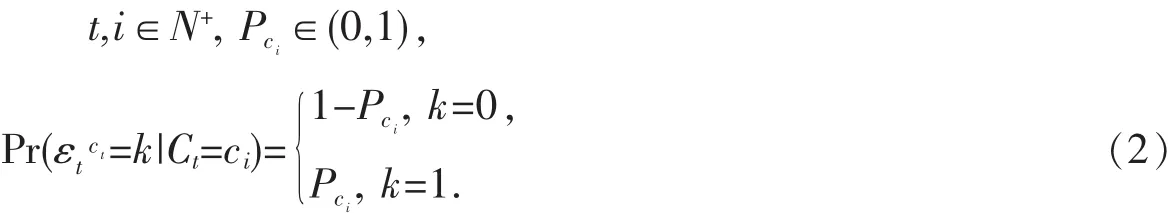
任意的时刻t,Θ表示可行的分红策略Φ的集合,则Φ是关于盈余x的函数[7].与实际结合,假设在t=0时不考虑分红,每个时刻分红的上界为.在Φ控制下破产时刻Γ前全部红利的期望贴现值为[7]:
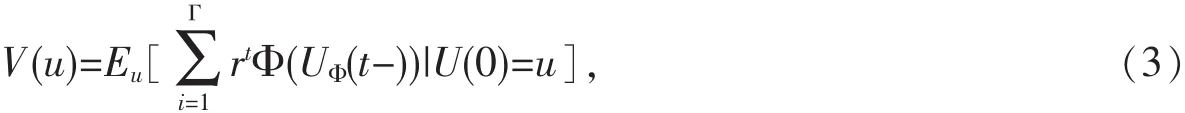
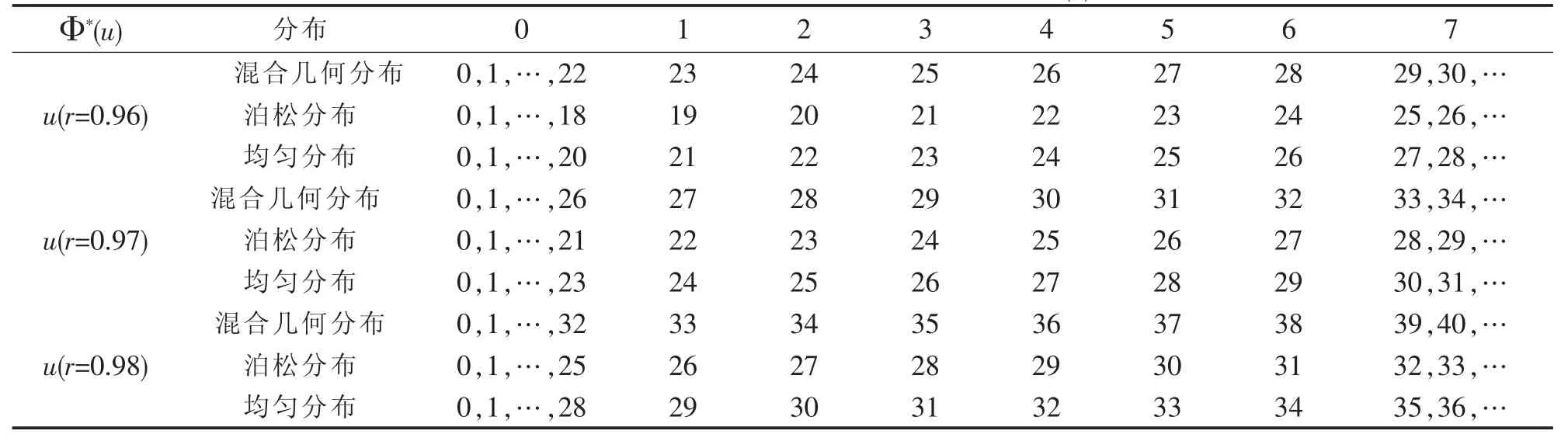
其中0 定理1 假设0 且对∀Φ∈Θ,u∈N,值函数V(u)最优当且仅当: 记最优的 Φ 为 ΦV[7]. 定义1 对∀X,Y∈H,d(X,Y)=‖x(u)-y(u)‖为H(N上的全体有界实值函数组成的集合)上的一个距离,显然∀Φ∈Θ,相应的值函数V(u)∈H,H=(H,d)是一个Banach空间.定义H上的算子T:则在0 根据式(4)和式(6),任意给定函数V(u)的一个初始值V0(u),运用Berman递归算法可由式(7)计算序列{V1(u),V2(u),…,Vn(u)…}: 由定义1知V*(u)是T的一个固定点,则,估计的精度为: V*(u)的方程中的x取值可趋于无穷,计算机编程计算有困难,因此,本文考虑V*(u)的近似值.定义2 ∀u,n0∈N,则: 由文献[8]知: 计算得误差的上限为:控制n0的值可确定估计的精度,即可要求d(V1*,V2*)→0.在数值计算中,当n0足够大时(可给定误差来确定),可以用V1*(u)或V2*(u)的值作为V*(u)的近似值. 对∀∈N,根据定义1给出两个满足压缩映射的算子T1和T2分别变换V1*(u)和V2*(u),运用不动点原理和递归算法,在R软件中就可以编程计算出V1*(u)或V2*(u)的值,本文给出了V1*(u)和V2*(u)的部分值,并给出相应结论. 例1 假设单位时间内支出Ct和对应的收入概率Pci的分布列如表1所示,收入均值为μ=17.5,要求=7. 表 1 Ct和 Pci的分布列 (2)假设收入是泊松分布. (3)假设收入是离散的均匀分布U(1,34). 给定误差(8)、(12)的上限为0.001,贴现因子r=0.96,0.97,0.98.在R软件中计算出3种分布下最优红利策略都为门槛策略,门槛值分别为:b1=22,26,32;b2=18,21,25;b3=20,23,28.符合分布的特点.因为均匀分布的概率不受收入的影响,混合几何分布的概率随着收入的增加逐渐减少,而泊松分布在收入均值17.5附近的概率值较大,在相同的模型、收入均值、误差上限和利率等条件下,混合几何分布的门槛值略高于泊松分布,泊松分布的门槛值又略高于均匀分布.又因为这里收入均值不大,因此它们之间的门槛值差距也不大,符合实际. (1)假设收入是混合几何分布,概率函数如下: 表2 3种分布下V1*和V2*的最优分红策略Φ*(u) 当r=0.97时混合几何分布V1*(u)和V2*(u)的部分值见表3,可看到V1*(u)和V2*(u)值非常接近,最优值函数V*(u)可通过V1*(u)或V2*(u)近似,这也说明了Berman递归算法的可行性.当资金较小时,每增加一单位,最优红利总值增加较明显,后期增长幅度逐渐下降,在分红有上界的限定下,V*(u)是增幅逐渐递减的递增函数.也可根据不同的问题设定合理的误差上限来提高精度. 表3 混合几何分布下V1*(u)和V2*(u)的部分值(r=0.97) 当r=0.97时离散均匀分布下的部分数值见表4.其他条件不变的前提下,当u较小时贴现因子的变动对总红利影响较显著,因为总注资过低公司的运营受外界影响因素波动较大,公司的资金大部分投入生产和避风险,分红量不够稳定,贴合实际. 表4 均匀分布下的部分值(r=0.97) 对偶模型是经典风险模型的一个延伸,本文讨论了随机投资下对偶模型的数值模拟,得出几种常用的离散分布的最优红利策略为门槛策略,在均值相同的时候得出的门槛值相差不大,与收入分布又有密切的联系,说明文中模型的可行性.实际问题中可以根据不同的情况确定收入分布,应用到公司的红利优化中.后期的研究还可考虑在公司破产前注资,随机利率等马氏优化决策方法.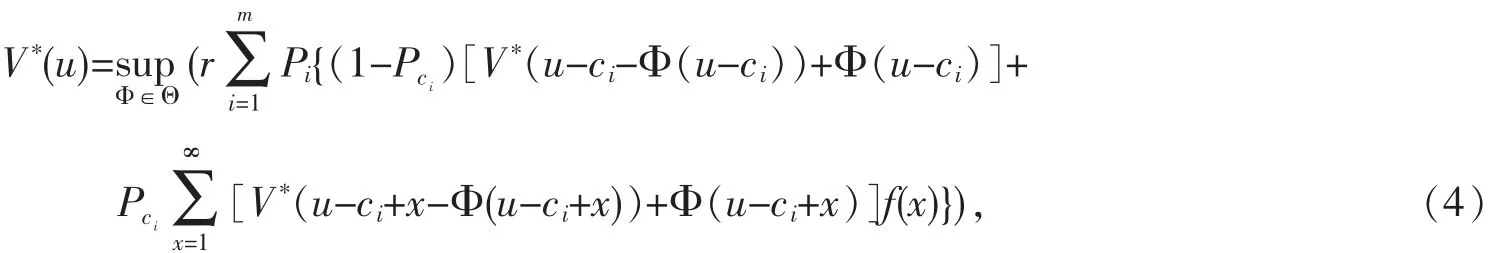

2 Berman递归算法

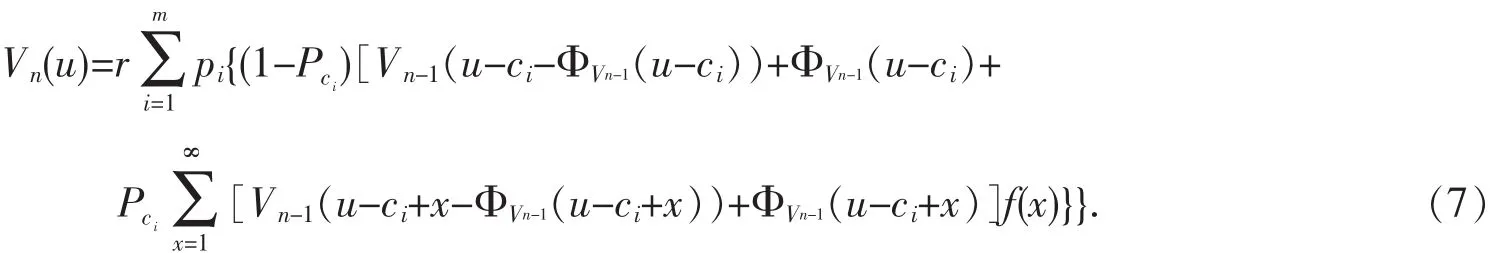

3 数值模拟
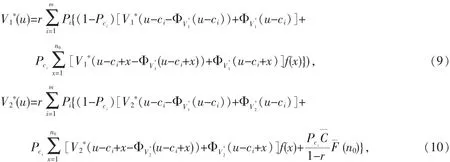






4 结论
