灰色关联—集对聚类预测模型在吉林省用水量预测中的应用

宋 帆， 杨晓华， 武翡翡， 孙波扬， 耿雷华

(1.北京师范大学 环境学院 水环境模拟国家重点实验室， 北京 100875； 2.南京水利科学研究院， 江苏 南京 210029)

1 研究背景

随着社会经济的快速发展和城市化水平的进一步提高，人们的用水需求也大为增加，水资源短缺已经严重制约了某些地区的经济发展，影响了居民的生活水平。对区域水资源进行规划时，用水量的预测是其中的一个重要内容，其结果直接影响到水资源决策的可靠性以及宏观经济规划的合理性，对地区水资源的可持续利用和城市可持续发展都有重要作用[1]。目前常用的用水量预测方法有灰色预测法[2-3]、神经网络法[4]、回归预测法[5]以及支持向量机法[6]等，近年来系统动力学[7]等动态模拟模型也逐渐被用到这方面来。除此之外，一些学者还将某些方法经过适当组合后应用于用水量预测，比如冯天梅等[8]利用灰色神经网络模型对包头市用水量进行了预测；Firat等[9]将神经网络与模糊运算相结合用于伊兹密尔市耗水量的探究，均取得了较好的效果。集对分析聚类预测法是结合集对分析联系度[10]及聚类思想的一种新的预测方法，它将预测对象及其影响因子的数据作为一个整体，共同进行数据处理，然后通过对影响因子的预测来估算预测对象未来的发展趋势。该模型具有较高的精度，并且在处理预测中的不确定性问题上有独特的优势。近些年来该方法被逐渐应用到各个领域，比如吴开亚等[11]和袁朝阳等[12]将集对分析聚类预测应用于安徽省生态足迹趋势的预测和山东省用水量预测中并获得了较高的预测精度，文虎等[13]利用集对分析聚类预测法综合多因素预测了煤与瓦斯突出。本研究为了克服传统模型在用水量预测中的结构不确定性问题，结合灰色关联度(Grey Correlation Degree)以及集对分析聚类预测法(Set Pair Analysis Classified Prediction Method)建立了用水量预测的灰关联-集对聚类预测模型(GCD-SPACPM),通过灰色关联度分析识别出吉林省用水量的主要影响指标，并用集对聚类法对吉林省未来一段时间用水量进行了预测，创新性地将二者结合在一起，为用水量预测提供了新思路。

2 GCD-SPACPM预测模型

2.1 集对分析理论

集对分析是赵克勤在1989年提出的一种研究确定性以及不确定性的系统分析思想。集对分析的本质是将确定、不确定性系统从同、异、反3方面分析其中的联系和转化[14]，并且通过对同异反联系度的计算来描述系统的不确定性，同异反联系度表达式为：

u=a+bi+cj

(1)

式中：a、b、c分别为同一度、差异度与对立度，代表了集对中集合的正趋势、不确定趋势与反趋势，且a+b+c=1；i为差异标记，取值于[-1,1]；j为对立标记，规定取值为-1。

2.2 灰色关联度分析

灰色关联度分析通常用来定量描述事物间的关联程度，关联度越大代表两类事物间的相似程度越高[15]，进而可以从原始变量中找出少数几个主要变量，将多指标体系简化以实现降维计算。由于灰色关联度分析具有对数据要求低及原理简单易于掌握的优点，因而得到了广泛应用。

灰色关联度分析的基本原理如下：一般设参考数列为X0={x0(k),k=1,2,…,n}，比较数列为Xi={xi(k),k=1,2,…,n}(i=1,2,…,m)，则两者间的关联度为：

(2)

(3)

式中：ξ为分辨系数，作用是削弱极大值对结果产生的影响，且ξ∈[0,1]；Δmax和Δmin分别为Δ0i(max) 和Δ0i(min)中的最大值和最小值，由下式计算[16-17]：

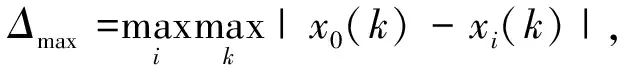
(4)

2.3 模型建立流程

GCD-SPACPM模型建立流程如图1所示。

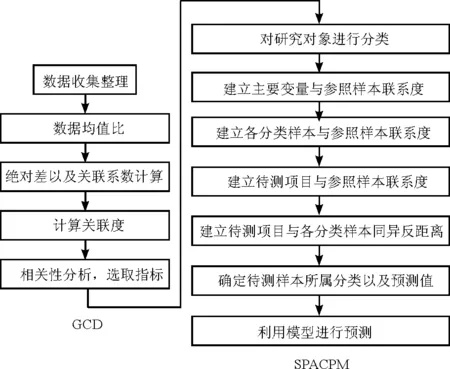
图1 GCD-SPACPM流程

(1)数据均值化。计算之前要将数据进行标准化处理，通常有初值化和均值化两种处理方式，前者适用于增减明显的数列，而后者应用在变化趋势不大的数列。本研究采用后者进行标准化处理，首先分别求出每个指标数列的平均数，再用数列的所有数据除以该数列的平均数，得到一个倍数数列，即均值化数列。

(2)计算关联度。根据公式(1)～(3)计算各个指标与用水量的关联度，并由此确定与用水量数列相似程度最高的指标。

(3)对预测对象进行分类。假设预测对象为N，根据用水量增长率将N分为n个分类，记为N={N1，N2，…，Nn}，要求各分类样本数目大致相等。

(4)建立各影响因素与参照样本的联系度。将预测对象N的增长率集合Xk={xkt|t=1,2,…,m} 与参照样本集合X0={x0t=1|t=1,2,…,m}相对比，在集对分析原理下制定二者的同异反联系向量。由于N中各分类集合都分别受到多种因素的影响，因此每个分类集合都应分别建立与各影响因素的联系度。第k个分类集合Nk与参照样本组成集对后关于第t个因素(t=1,2，…，m)的联系度表示为：

ukt=akt+bkti+cktj

(5)

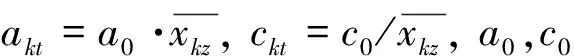
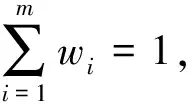
uk=w1uk1+w2uk2+…+wmukm

=ak+bki+ckj

(6)

(6)建立待测项目与参照样本的同异反联系度。假设共有p个待测项目,参考步骤(4)和(5)分别对每个项目建立加权同异反联系度如下：

ul=w1ul1+w2ul2+…+wmulm

=al+bli+clj

(7)

(l=1,2,…,p)

(7)计算待测样本对各分类集合的同异反距离。设第l个待测样本与第k个分类集合的同异反距离为ρkl，则：

(8)

(k=1,2,…,n;l=1,2,…,p)

(8)确定待测样本分类以及预测值。按照同异反模式里的“择近原则”，待测样本与N中的哪一个分类距离最近就将其归为哪类。用xk0代表每个分类系统的中心值，则待测样本的预测值为[20]：

(9)

3 模型应用

3.1 研究区概况

吉林省地处中国东北部，土地面积18.7×104km2，2015年末总人口为2 753.32×104人。2015年吉林省全省水资源总量为295.04×108m3，占全国水资源总量的1.094%，但全省用水量为133.56×108m3，占全国总用水量的2.18%。就人均来看，吉林省2015年人均水资源占有量为1071.58 m3，仅为全国人均水资源占有量的52.7%。总的来说，吉林省水资源占有量少但用水量较大，属于中度缺水地区，而且吉林省水资源分布“东丰西欠”，时空和季节分布严重不均，水资源短缺已经成为制约吉林省经济发展的重要因素，对用水量进行准确预测对于吉林省水资源的可持续发展有重要意义。

3.2 指标选取及灰色关联度分析

为了全面涵盖各方面的影响因素，本研究指标选取综合考虑了农业、工业、生活3个方面，选取有效灌溉面积(103hm2)、单位灌溉面积用水量(m3/hm2)作为农业用水驱动因素；人均日生活用水量(L)、总人口(104人)作为生活用水驱动因素；工业产值(108元)、万元工业增加值用水量(m3)作为工业用水驱动因素；另外考虑到经济因素将人均GDP(元)作为经济指标加入指标体系。

将吉林省1996-2015年各指标数据作为原始数据，利用灰色关联度分析对各指标与总用水量之间的相似程度进行估算，各指标关联度计算结果如表1所示。由表1中计算结果可知，各指标与用水量之间的相似程度大致分为3个等级：第1级相似程度最高，包括有效灌溉面积和常住人口两个指标，灰色关联度超过了0.83；第2级相似程度中等，包括单位灌溉面积用水量和人均日生活用水量两个指标，灰色关联度介于0.7～0.8之间；第3级相似程度很低，包括人均GDP、工业产值和万元工业增加值用水量3个指标，灰色关联度低于0.6。因此选取有效灌溉面积和常住人口两个指标作为后续计算的基础数据。

3.3 样本分类处理

吉林省1996-2015年用水总量、有效灌溉面积、总人口3个指标各年变化率见表2。将表2中1996-2014年数据作为分类样本建立模型，并将2015年的数据作为待测样本用来预测对比。

根据表2数据可知吉林省1996-2014年用水量增长率在0.9301～1.0934范围内，将该样本分为5类，在分类时使各个类别中的样本数量尽量相等，分类结果如表3所示。

3.4 建立各类样本与参照系统的同异反联系度

假设第k个(k=1,2,3)分类集合Nk与参照样本组成集对后关于第t个(t=1,2)因素的联系度表示为ukt=akt+bkti+cktj，根据表2数据可得各类样本单因素同异反联系度如下(以第一类样本为例)：

表1 各指标灰色关联度计算结果

表2 吉林省1996-2015年用水量、有效灌溉面积及常住人口数据

表3 各分类样本及其各影响因素年增长率的平均值

u11=0.5234+0.2855i+0.1910j

u12=0.5020+0.2988i+0.1992j

为避免主观赋权导致的结果不客观性，对两个影响因素做等权重处理，由此可得出各分类样本(N1，N2，N3)与参照系统组成集对后的联系度，结果如下(以第一类样本为例)：

u1=0.5127+0.2922i+0.1951j

3.5 计算待测样本与参照系统的同异反联系度

为测试灰关联-集对聚类预测模型的精度，以2015年吉林省单位灌溉面积用水量、有效灌溉面积的年增长率为待测样本的观测值。确定该待测样本与参照系统构建集对后对第t个因素(t=1,2)的联系度分别为:

ux1=0.5498+0.2683i+0.1819j

ux2=0.5002+0.2999i+0.1999j

同理在给两个要素赋予相等权重后可得到待测样本与参照系统的联系度为：

ux=0.5250+0.2841i+0.1909j

3.6 计算预测值及结果分析

根据上文所得联系度可计算待测样本与各分类样本的同异反距离(表4)，再根据公式(9)可预测2015年吉林省用水量增长率为1.0245。

表4 待测样本与各分类样本同异反距离以及预测增长率

3.7 结果分析

根据灰关联-集对聚类模型预测的吉林省2015年用水量年变化率为1.0245，而当年用水量增长率实际值为1.0044，相对误差为2.00%，预测精度较好，如果根据实际情况充分考虑权重分配可进一步提高精度。

为了验证模型的预测精度，在此与其他常用预测模型结果进行了对比。利用相同的历史数据，分别采用灰色预测模型GM(1,1)和BP神经网络对吉林省2015年用水量增长率进行预测，结果如表5所示。

表5 灰色模型和BP神经网络预测结果

由表5可知，在本次探究中灰关联-集对聚类预测模型预测效果优于灰色预测模型，略优于BP神经网络预测模型，可见将该方法应用在不确定性分析预测中是有效合理的。

3.8 结果交叉验证

与其他预测模型相比，灰关联-集对聚类预测模型的另一个优点是可以不受时间序列的限制，根据建模的基础数据可预测任意年的用水量数据。为了证明这一优点，并且进一步验证模型预测的合理性，本次研究采用交叉验证的方法，将每一年的用水量数据分别作为待预测数据，其余n-1年数据作为建模基础数据，验证模型预测精度如表6所示。

由表6数据可知，20 a预测结果平均误差为2.675%，个别年份误差较大，经过研究发现是在样本极值所在年份(2001及2011年)及其附近年份，但总体预测效果良好。因此，将灰关联-集对聚类方法用在吉林省用水量预测中是合理的，若对极值进行相关换算则结果会更加理想，这也为今后进一步提高预测精度提供了新思路。

表6 模型交叉验证预测结果 %

3.9 拓展预测

模型建立完成后将其用于吉林省短期内的用水量预测。根据吉林省农业委员会编制的《吉林省农业可持续发展规划(2015-2030年)》，到2020年，全省有效灌溉面积将增加到200×104hm2。由此推算2016-2020年吉林省有效灌溉面积变化率为1.023。根据国务院印发的《国家人口发展规划(2016-2030年)》，2020年人口总量大约是2015年的1.033倍。参考吉林省人口现状以及引进人才计划，采用比全国人口增长率略高1%的人口增长率进行测算，即1.017。由此推算吉林省2016-2020年用水量趋势如图2所示。

图2 吉林省2016-2020年用水量预测结果

由图2可知，到2020年吉林省用水量为138.74×108m3，增长势头有所放缓，此时需水模数将达到7.4×104m3/km2，水资源承载状态依旧严峻。因此吉林省当地必须要制定合理的水资源利用保护规划来避免用水量的过快增长以及水资源状况的恶化，同时要将水污染治理与水资源保护形成合力，提高中水回用比例，形成水资源的多级利用体系。

4 结 论

(1)灰关联-集对聚类预测模型对于2015年用水量数据预测误差为2.00%，优于灰色预测模型和BP神经网络模型。并且经过20 a数据的交叉验证得到平均误差为2.675%，预测精度良好，能克服传统参数统计预测模型的结构不确定性问题。经过拓展预测，得到2020年吉林省用水量为138.74×108m3，预测结果可为当地预测期内的城市水资源合理利用与配置提供理论依据。

(2)灰关联-集对聚类预测模型将两种模型的优点集于一身。既可识别影响用水量的关键因子，从而减少工作量并提高预测精度，也可以根据建模基础数据预测未来数据或者补全历史丢失数据，应用比较简单、实用性强，为长期预测模型的建立提供了新思路，并且对集对分析聚类预测模型的应用有了进一步扩展。

(3)研究发现灰关联-集对聚类预测模型对于极值的处理还存在一定缺陷，建模样本数据较少时的准确性有待考证，并且在权重确定上还有待进一步探究，这也是本研究方向今后的工作重点。