FSC赛车半轴设计与分析

（常熟理工学院，苏州 215500）

0 引言

中国大学生方程式汽车大赛[1]（简称FSC）是由中国汽车工程学会主办的面向全国高等院校的赛事。2017年共有72所高校参与FSC，2018年将有78所高校参加比赛。该赛事有众多奖项，其中颁有轻量化奖项。而一辆FSC赛车由动力系统和底盘系统等组成，其中每一个零部件都需要经过精心设计和分析，确保在安全使用的条件下获得最小的重量和最优的性能。驱动半轴作为FSC赛车底盘传动系统的一个零件，位于主减速和车轮之间，其作用是将发动机输出的扭矩经过主减速器、差速器传递给车轮。因此半轴的轻量化在FSC赛车设计中是并不可少的一个环节。轻量化的半轴，不仅可以显著地减轻整车重量，而且可以有效减小传动系统的转动惯量，从而提高传动系统的响应速度。半轴的轻量化可从两个环节着手：一个环节可采用密度较小，但强度不低的材料，如碳纤维材料；另一个环节可从结构设计方面着手。

通过对主减速器传动比进行优化，根据不同赛道下对半轴的最大承受扭矩进行计算。通过理论计算确定半轴的最大承受扭矩，以及半轴的直径，并通过ANSYS Workbench对半轴进行有限元分析，提出改进意见，该改进方案应用于2017年FSC赛车上，在效率测试项目上获得较高的成绩。

1 主减速器传动比的优化

FSC动态赛分为75米直线、8字环绕、高速避障、耐久测试、以及效率测试[2]。其中高速避障与耐久测试的赛道相仿，效率测试为计算耐久测试所消耗的燃油量；8字环绕主要考虑赛车的操控性，在此不予考虑。直线加速和耐久测试所需的主减速器比是不同的，可在Optimum Lap中建立整车数据、空气动力学数据、轮胎数据、发动机数据、传动系统数据，并分别在直线加速赛道和德国霍根海姆赛区耐久赛道进行模拟。其模拟的参数如图1、图2所示。

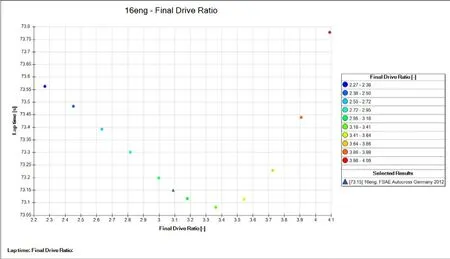
图1 耐久测试单圈时间与主减速器传动比的关系

由图1可见，随着主减速器传动比的增加，耐久单圈时间先减小后增加，当主减速器传动比为3.4的时候，耐久单圈时间最少，但时间相差在0.6秒以内。由图2可见，随着主减速器传动比的增加，直线加速时间先减小后增加，当主减速器传动比为3.1的时候，直线加速时间最少，直线成绩最高可以提高0.3秒。考虑到较小的主减速器传动比拥有较好的经济性，且可有效地减小大链轮的尺寸，从而带来减小传动系统的质量、利于赛车布置等优势，所以选用的主减速器传动比为3.1。通过选用11齿的小链轮、34齿的大链轮，主减速器传动比最终确定为3.09。

图2 直线加速时间与主减速器传动比的关系

2 半轴最大扭矩和理论直径计算

FSC赛车的半轴所承受的最大扭矩可能出现在两个工况，即工况一：在水平路面上以最大驱动力矩起步；工况二：在过弯时，变速器处于二档，发动机以最大扭矩输出，差速器锁死，此时单边半轴会承受较大的扭矩。通过比较两种工况半轴所需要承受的最大扭矩，取较大值作为半轴设计理论条件。

2.1 工况一

FSC赛车为后轮驱动，在水平赛道起步时，其后驱动轮的法向反作用力为：

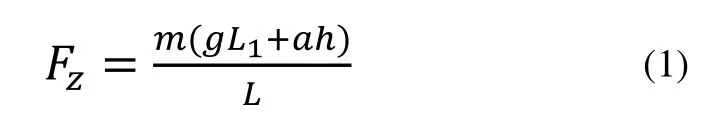
其中：m为赛车质量，取290kg；g为重力加速度，取9.8m/s；a为赛车水平加速度；h为赛车质心高度，取280mm；L1为质心到前轴的距离，取821.6mm；L为赛车轴距，取1580mm。

地面提供的最大切向反作用力为：

当地面所提供的最大切向反作用力全部用于赛车加速时，即：

切向反作用力Fx作用于驱动桥的扭矩为：

由式(1)～式(3)可推导出：

所以：

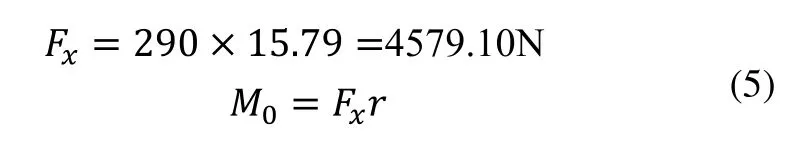
其中：M0为赛车起步时地面所能提供的最大驱动力矩；r为轮胎半径，取0.232m。

一档起步时发动机所能提供给驱动桥的最大扭矩为：

其中：Tmax为发动机提供的最大扭矩，取48.33N.m；i0为发动机初始传动比，取2.11；i1为变速箱一档传动比，取2.75；ig为主减速器传动比，取3.09；为传动效率，取0.95，则有：

由上可得M1＜M0，即起步瞬间，发动机提供的扭矩小于地面所能提供的最大驱动力矩。所以最大驱动力矩为M1=823.216N.m。对于德雷克斯勒差速器，当左右半轴输出转速相同时，其扭矩均匀分配到左右半轴。由于水平赛道起步时，左右半轴可视为转速相等，所以半轴所承受的扭矩即M为411.61N.m。

2.2 工况二

稳态时后轮的法向反作用力为：

此时地面所能提供的附着力：

附着力作用于驱动桥的扭矩为：

由式(7)～式(9)可推导出：

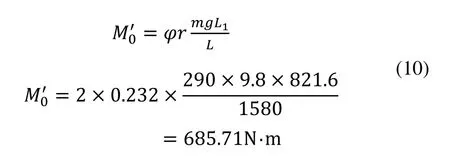
二档时发动机能提供给驱动桥的最大扭矩为：

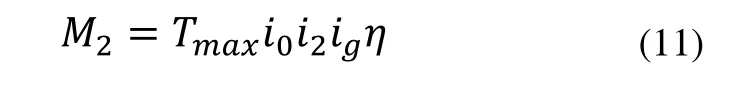
i2为主减速器二挡传动比，取2。

由上可得M2＜M0'，即发动机提供的最大力矩全部用于驱动车轮。

对于德雷克斯勒差速器，赛车前行时选用的Ramp angles为45°，其对应的锁紧扭矩百分比ca=51%。可得单边半轴所承受的最大扭矩为M'=0.51M2，即M'为305.34N.m，小于M。

综上，以M的值411.61N.m作为半轴的设计理论条件。

2.3 半轴理论直径计算

对于韧性材料d切应力计算公式[3]为：

半轴的直径：

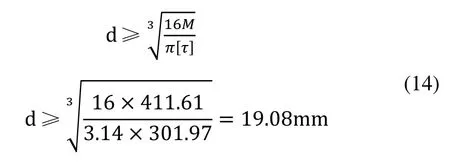
选用轴的直径为20mm。

3 半轴建模

半轴花键可通过CAXA中选用齿形命令，输入相应参数，建立外花键单齿轮廓，并将文件导出中间格式。在CATIA中导入该中间格式文件，建立半轴三维数模，生成igs文件。半轴的三维数模如图3所示。

图3 半轴三维数模

4 半轴有限元分析

在Engineering Data中建立材料40Cr，并输入弹性模量2.11×1011、泊松比0.277。利用CAD/CAE之间接口，将半轴的igs三维数模导入ANSYS Workbench软件中。采用网格密度为1.5mm的四面体网格，划分后的网格质量大于0.8。在半轴的一端花键齿面施加Fixed Support约束，在另一端对应的齿面施加大小为411.610N.m的扭矩。有限元分析结果如图4所示。

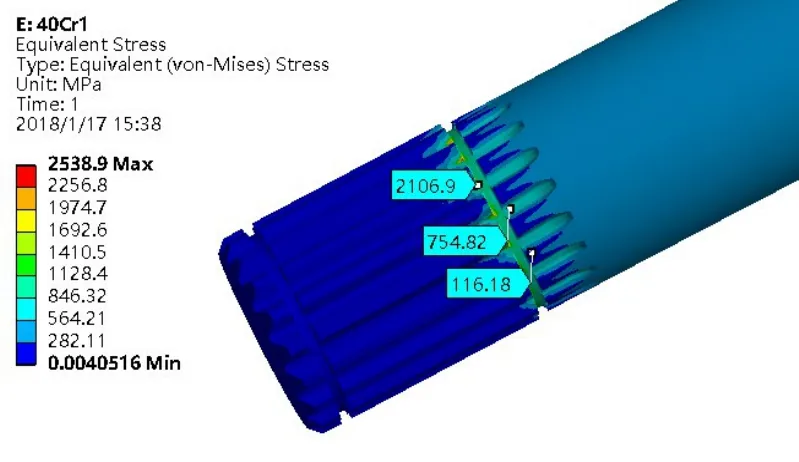
图4 Equivalent Stress云图分布（1）

由图4可知，花键局部应力过大，远超过40Cr的屈服应力。其尖端应力过大的现象是由有限元奇异性所产生的，但它并不是真实应力。因此需对有限元分析的边界条件进行重新设定。在CATIA中建立与半轴花键相匹配的简化零件，装配后导入ANSYS Workbench中，如图5所示。

图5 半轴与其匹配零部件的装配图

在ANSYS Workbench自动生成的接触，对外圆柱面施加Fixed Support约束，对另一端外圆柱面施加411.610N.m的扭矩，如图6所示。经有限元分析，其最大值为1001.5MPa，如图7所示。

40Cr的屈服强度为785MPa，有限元分析结果大于材料的屈服强度，不符合使用要求。为满足分析要求以及轻量化需求，可选用密度更小，屈服强度更高的TC4材料。其有限元分析的最大值为1060.9MPa，分析的应力值虽然有所增加，但热处理后的TC4材料屈服强度为1100MPa，故满足设计要求。其有限元分析结果如图8所示。

图8 Equivalent Stress云图分布（3）

5 半轴扭转角校核

半轴横截面的极惯性矩：

d为半轴杆部直径20mm。

半轴的最大扭转角：

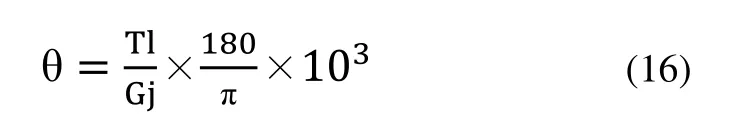
G为材料的剪切弹性模量，其值为41045MPa，l为半轴长度，其值为416mm。

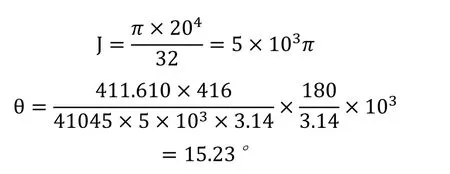
经计算θ的值为15.23°，考虑到计算采用的是最大扭矩情况下，故该值在允许的范围内。

6 结论

利用Optimum Lap优化了主减速器传动比，从而确定半轴的最大扭矩和直径。运用ANSYS Workbench软件对半轴进行有限元分析，分析认为若半轴采用40Cr，则设计不安全。因此采用屈服强度更大的TC4材料，一方面能减轻半轴重量，另一方面其强度满足使用要求。该半轴应用在2017年FSC赛车中，整个赛况未出现异常，且在效率测试项目上获得较高的成绩。