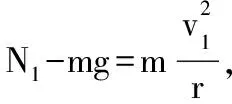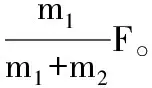力学中的几个常见的定值模型

江西 陈 明

高中力学题中有一些题目的题型差不多，解题思路、方法相似，而且有一些题目的结论是定值。如果能找到这一类题目的规律，建立模型，那么在解答这一类的物理问题时就能够非常快速地找到方便、准确、简单的方法。本文将对高中力学中的几个常见的定值模型进行分析。

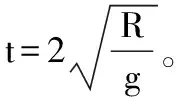
【解析】对于同一圆，半径一定相等。选取任意情况进行研究分析

△ABE为直角三角形，EA、AB的夹角为θ。圆的半径为R，则物体从E到B下滑的加速度a=gsinθ，到达B点的位移为x=2Rsinθ

故物体下滑时间为定值，只与半径有关，与轨道倾角大小无关。

【解析】对物体从A点运动至B点过程，应用动能定理，有：

对物体从B点运动至C点过程，应用动能定理，有：

【模型三】两个质量不同的小球用长度不等的细线拴在同一点并在同一水平面内做匀速圆周运动，如图3所示，则它们的运动角速度(周期)相同。

【解析】对其中任意一个小球受力分析，如图4所示

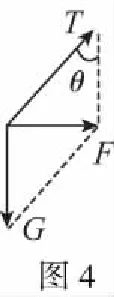
小球受重力mg、绳子的拉力T，由于小球做匀速圆周运动，故两个力的合力提供向心力

将重力与拉力合成，合力指向圆心

由几何关系得，合力F=mgtanθ

设绳长为L，由向心力公式得到

F=mω2r=mω2Lsinθ

由于两小球在同一水平面内做匀速圆周运动

故两小球做圆周运动的角速度(周期)为定值，与绳子的长度、转动半径均无关。

【模型四】如图5所示，OA为遵从胡克定律的弹性轻绳，其一端固定于小车的架子上的O点，另一端A与一小球相连，系统处于平衡状态，BO为一轻质硬管，BO长度等于弹性绳的自然长度。现使小车从静止开始向左加速，加速度从零开始迅速增大到某一值，然后保持此值，小球稳定地偏离竖直方向某一角度(弹性绳在弹性限度内，不计弹性绳与BO间摩擦)。与开始稳定在竖直位置时相比，小球的高度将不变。

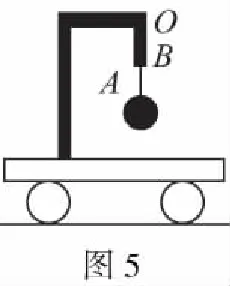
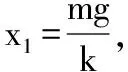
当小车的加速度稳定在一定值时，对小球进行受力分析如图6所示，得：

T2cosα=mg，T2sinα=ma

则小球与悬挂点的竖直方向的距离为：

L2=L0+x2cosα

即x2cosα为定值。

所以L1=L2，即小球在竖直方向上到悬挂点的距离不变，所以小球高度将不变。

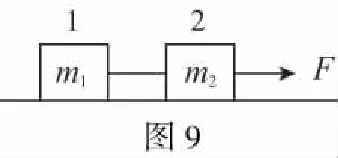
【模型五】在光滑水平面上有一静止的物体。现以水平恒力甲推这一物体，作用一段时间后，换成相反方向的水平恒力乙拉这一物体，当恒力乙作用时间与恒力甲作用时间相同时，物体恰好回到原处，则在整个过程中，恒力乙与恒力甲的大小之比为3∶1，恒力乙与恒力甲分别做的功之比为3∶1。

【解析】设第一过程末速度为v1，第二过程末速度大小为v2。因两阶段运动位移大小相等，时间间隔又相等，所以两过程运动的平均速度大小必相等，即

即得W1=Ek1,W2=Ek2-Ek1=3Ek1

所以W2=3W1,F2=3F1

此过程中，恒力乙与恒力甲的大小之比，相应的力的冲量大小之比，相应的加速度大小之比，相应的力做功大小之比都一样，都为3∶1。

【模型六】如图7所示，一根不可伸长轻绳，一端系于天花板O点，另一端系一个质量为m的小球，小球从水平位置由静止释放。不计一切摩擦，当小球经过最低点时，小球对绳的拉力为F=3mg，大小不变。

【解析】小球摆动过程中，只有重力做功，机械能守恒，则有：

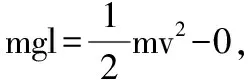
可得F=3mg

根据牛顿第三定律有：

F′=-F=-3mg

小球对绳的拉力大小为3mg，方向竖直向下

小球只在重力作用下从水平位置由静止摆到最低点，经过最低点时对绳的拉力为定值3mg，与绳长无关。

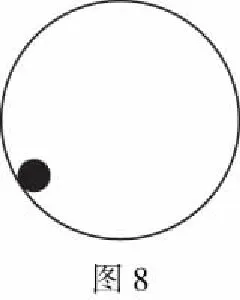
【模型七】(2016年海南卷)如图8所示，光滑圆轨道固定在竖直面内，一质量为m的小球沿轨道做完整的圆周运动。已知小球在最低点时对轨道的压力大小为N1，在高点时对轨道的压力大小为N2。重力加速度大小为g，则N1-N2的值为6mg。