云环境下代理加密模糊检索研究

李陶深，王 翼，黄汝维

(1.广西大学计算机与电子信息学院 南宁 530004；2.广西高校并行分布式计算技术重点实验室 南宁 530004)

数据加密是云环境下一种常用的保护数据隐私的方法，但该方法的缺陷是用户不能对加密数据进行检索操作。为解决加密检索问题，可搜索加密(searchable encryption，SE)算法应运而生，它可解决当数据加密存储在云端时，服务器不完全可信情况下完成安全的关键词搜索[1]。SE技术可分为单用户SE技术、多用户SE技术、模糊加密搜索技术3类。

在多用户SE技术方面，文献[2]提出一种云存储环境下的多用户可搜索加密方案，使得经过用户加密的数据只在必要时才会被重新加密，减少了加密的计算量。文献[3]对文献[2]的方案进行优化，提出一种改进的多用户可搜索加密方案，让用户管理及密钥分配中心参与处理用户的搜索请求，降低了云服务器的开销，提高了搜索效率。文献[4]提出一种匿名的多用户加密搜索方案，对搜索用户的信息进行加密，使服务器端不知道哪个用户搜索了哪些信息，提高了安全性。文献[5]提出一种对称加密的多用户加密检索方案，实现了云存储环境下的多用户对加密关键词的搜索功能。文献[6-7]提出基于属性的多用户加密搜索方案，利用一些属性去加密文件，加密者无需知道解密者的身份，只要用户满足密文属性就能解密文件，保证了数据的安全。文献[8]提出一种适用于数据存储的代理重加密方案，通过消除冗余陷门生成算法和简化解密算法来降低计算复杂度，提高系统效率。文献[9]提出一种自主授权的多用户可搜索加密方案，利用半诚实的云服务器来维护一个权限分配矩阵，弱化了可信第三方的功能。文献[10]提出一个可验证的基于词典的可搜索加密方案，用于解决云存储中数据检索和安全问题。上述的多用户加密搜索方案只能进行精确关键字的检索，不允许用户有拼写错误情况，不支持模糊检索。

在云环境的模糊检索加密方面，文献[11]在文献[3]方案的基础上，利用双线性映射以及布隆过滤器技术，提出一种支持相似度搜索的模糊检索方法。文献[12]提出了一种基于索引构建技术的模糊检索机制，可降低计算开销。文献[13]提出一种基于字典的模糊集算法，在减小索引文件基础上实现加密数据的模糊搜索。文献[14]提出一种基于局部敏感哈希技术的关键词模糊搜索方案，实现了多关键字下隐私保护的模糊检索功能。文献[15]采用布隆过滤器来构造安全索引进行检索，提出一种适用于云环境的可验证可搜索加密方法。文献[16]提出一种云环境下满足多用户分享数据需求的多用户模糊检索加密方案。上述的模糊检索加密机制大多是通过共享密钥的形式去解密搜索到的加密数据，一旦某个用户的密钥遭到泄露，整个系统的密钥都需要更换，工作量较大。同时，在安全性方面也存在缺陷，构造关键词模糊词集也会增加系统存储开销。

本文对云计算环境下多个关键词模糊检索可搜索加密算法进行研究，改进现有的基于通配符技术的模糊检索算法，提出一种适用于云计算环境的基于局部敏感哈希技术的代理加密模糊检索算法。

1 系统模型和问题描述

1.1 系统模型

设定云环境下密文检索系统框架如图1所示。图中有3类实体。

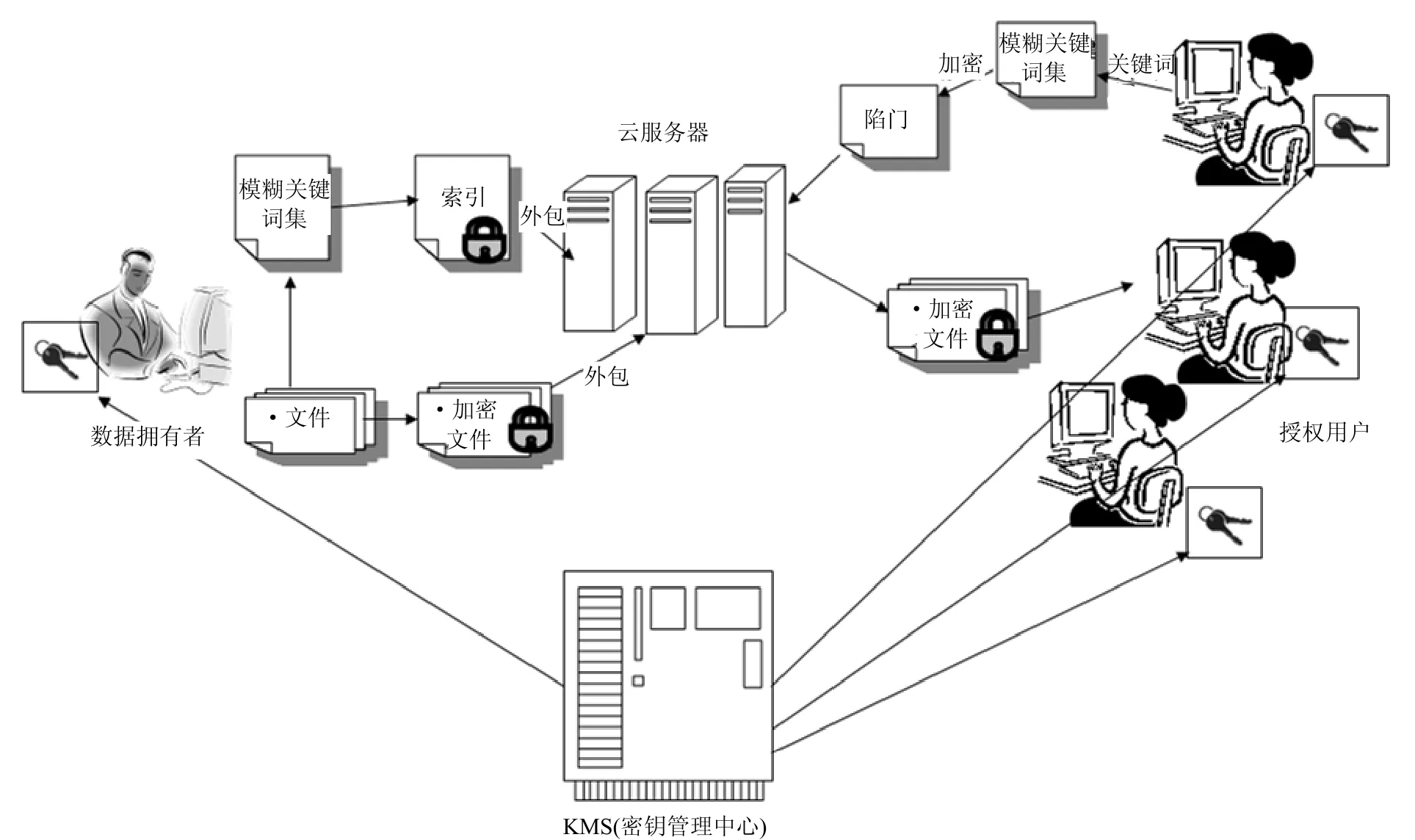
图1 云环境下密文检索框架

1)用户：授权用户是完全可信的，他们能够加解密、搜索和修改保存在云服务器上的加密数据。

2)服务器：主要责任是根据授权用户的搜索请求检索存储在其上的加密数据。数据存储服务器是不可信的，它可以正确地执行授权用户的请求，但是不能保证服务器自身不分析数据。

3)密钥管理中心(key management service,KMS)：一台可信任的服务器，负责生成和管理用户密钥，为每一个授权用户生成密钥并将密钥安全分发至用户手中。

图1中，数据所有者有n个文件，并要将这些文件以密文形式发送给云服务器，每个文件都定义了一组关键词W=(w1,w2,…,wn)。为了在服务器上进行有效检索，在将这些文件发送给云服务器前，数据拥有者首先为每个关键词建立一个安全索引I，然后将所有文件及索引发送给云服务器。当一个授权用户输入一个检索请求去搜索他感兴趣的加密文件时，云服务器将该请求映射到相关的加密数据文件。为搜索到相关文件，授权用户输入关键词，且需要生成一个搜索陷门Tw，然后将Tw发送给服务器。服务器收到Tw后就搜索索引，返回相关的加密文件。为提高搜索效率，可根据关键词进行模糊检索。

1.2 问题的描述

1.2.1 系统威胁

由图1所示的密文检索系统框架可以分析出云环境中可能存在两类隐私攻击：第一类是外部攻击，即用户的数据在网络传输过程中可能会被攻击者通过某种非法手段截取；第二类是内部攻击，即用户数据存储在云服务器上，云服务器有足够权限去访问存储在其上的用户加密数据，它有可能试图通过用户的请求去获取一些相关敏感信息。对于第一类攻击，攻击者获取的数据是经过加密的，如果没有解密密钥，则无法破解。本文主要考虑第二类攻击。

1.2.2 关键词集作为索引带来的开销

现有的模糊搜索机制大多建立一个可扩展的关键词集作为索引，该关键词集包含了所有用户可能拼写错误的关键词，这就使索引文件变得非常巨大，增加了系统存储开销和检索的复杂度。

1.2.3 布隆过滤器

布隆过滤器(Bloom filter, BL)是一种索引结构，由一个很长的二进制向量和一系列随机映射函数组成[15]。实际上，它是一个m位的集合，所有位数初始化时都设置为0。给定一个元素集合S={a1,a2,…,an}，其中ai(i=1,2,…,n)是某一个元素。一个布隆过滤器就会从哈希函数群H={hi|hi：S→[1,m], 1≤i≤l}中选出l个独立的哈希函数，通过将所有hi(a)对应位上的值设为1，将一个元素a∈S插入到布隆过滤器中。为了检测元素q是否存在于S中，l个哈希函数就会生成l地址位的值，如果任何地址位的值为0，那么q∉S；反之，q∈于S或者q定位错了地址。

1.2.4 局部敏感哈希技术

给定一个欧几里得距离向量d，LSH函数则会映射到概率较高、哈希值相同且距离近的向量，而不会映射到远距离的向量。利用p-stable LSH群技术，一个p-stable LSH函数的表示形式为：

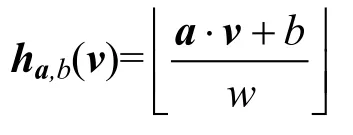
式中，a、v为向量；b、w为数字。

2 算法的设计与实现

2.1 算法设计思想

针对现有的模糊加密检索机制存在的存储容量需求过大的问题，本文设计一个适用于云环境的基于局部敏感哈希技术的代理加密模糊检索算法(PEFRA-LSH)。算法的设计目标如下：

1)允许多个用户通过自己的密钥去加密和解密检索相关文件，实现多个用户之间共享文件。

2)能够满足多个关键词的模糊检索需求，即使用户拼写有小的错误，所需求的文件也能被检索到。

3)不需要预先构建模糊关键词集，以便尽可能避免增加系统的存储开销及检索的复杂性。

4)云服务器不会从加密文件和索引中获取额外的敏感信息，以实现隐私保护的目标。

算法设计思想是：利用局部敏感哈希技术和布隆过滤器来构造一种支持多关键词的模糊检索方案,先将每个关键词转换成双字母向量形式，利用欧几里得距离获得关键词之间的相似度；再利用LSH函数代替标准哈希函数，将关键词插入到布隆过滤器中，并构建文件索引，使得算法不必预先构建模糊关键词集也能高效查找到与关键词相关的文件。

2.2 算法操作过程

PEFRA-LSH算法的主要操作过程如下：

1)转换且生成索引。为支持多个关键词模糊检索，数据拥有者首先将每个关键词转换成一个双音节集合。将该集合分为两部分，然后用密钥K1和K2为每部分加密形成索引，两部分索引组成加密索引文件。最后，将加密数据和加密索引上传到服务器。

2)为了检索关键词w，授权用户同样将检索关键词w转换成一个双音节集合，使用同样的密钥K1和K2加密相关部分形成陷门并上传到服务器。

3)检索匹配。云服务器收到搜索请求后，根据内积匹配算法，将索引与查询的加密形式做内积运算，如果两部分索引与查询的内积值等于原来的索引与查询的内积值，则匹配成功，返回所有相关的加密过的文件标识，用户解密它们得到想要的文件。即使拼写错误的查询关键词同样能够精确匹配到包含正确关键词的索引，并返回相关的加密文件。

2.3 算法的关键技术实现

下面以与“network”相关的文件和拼写错误的查询关键词“netword”为例，说明算法的实现。在本文算法中，为每一个文件D建立索引ID，该索引包含文件D中所有的关键词，是一个m位的布隆过滤器。

2.3.1 关键词的双音节向量形式

在本文算法中，建立索引的第一步是将每个关键词转换成一个双音节集合，该集合包含了该关键词中所有的连续两个字母组成的字符串。例如，关键词“network”的双音节集合为{ne,et,tw,wo,or, rk}。根据LSH函数的特点，算法使用26×26位长的向量表示双音节集合，集合中每个双音节都代表了26×26位长集合中一个可能的双音节。如果一个关键词对应的双音节存在于双音节集合中，那么就将该双音节设置为1。这种基于关键词形成的双音节向量对拼写错误的位置并不敏感，例如，错误的“nwtwork”、“netword”等都会被映射到一个向量中，该向量与“network”对应的向量存在两个双音节的差别，仍然是与正确的关键词最接近的向量形式，这个最接近的距离可用欧几里得距离衡量。这种双音节的向量形式是健壮的，关键的是能使用LSH函数来处理。

生成索引时，算法使用LSH函数h1、h2生成索引文件以及查询文件。由于两个向量形式之间的欧几里得距离在预设定的距离范围之内，利用LSH函数ha,b(v)，可以使得关键词“network”和拼写错误的查询关键词“netword”具有相同的哈希值。

2.3.2 索引的布隆过滤器形式

布隆过滤器通常被用于建立文件的索引，或者用于对单个关键词进行精确检索的场景中。一般的哈希函数只能用于检索精确的关键词。本文PEFRA-LAS算法由于采用了LSH函数来建立索引文件，它能将具有限定阈值且相似的输入以较高概率哈希到相同的输出中。图2显示了拼写错误的查询关键词“netword”被映射到与正确关键词“network”相同区域的示意图。

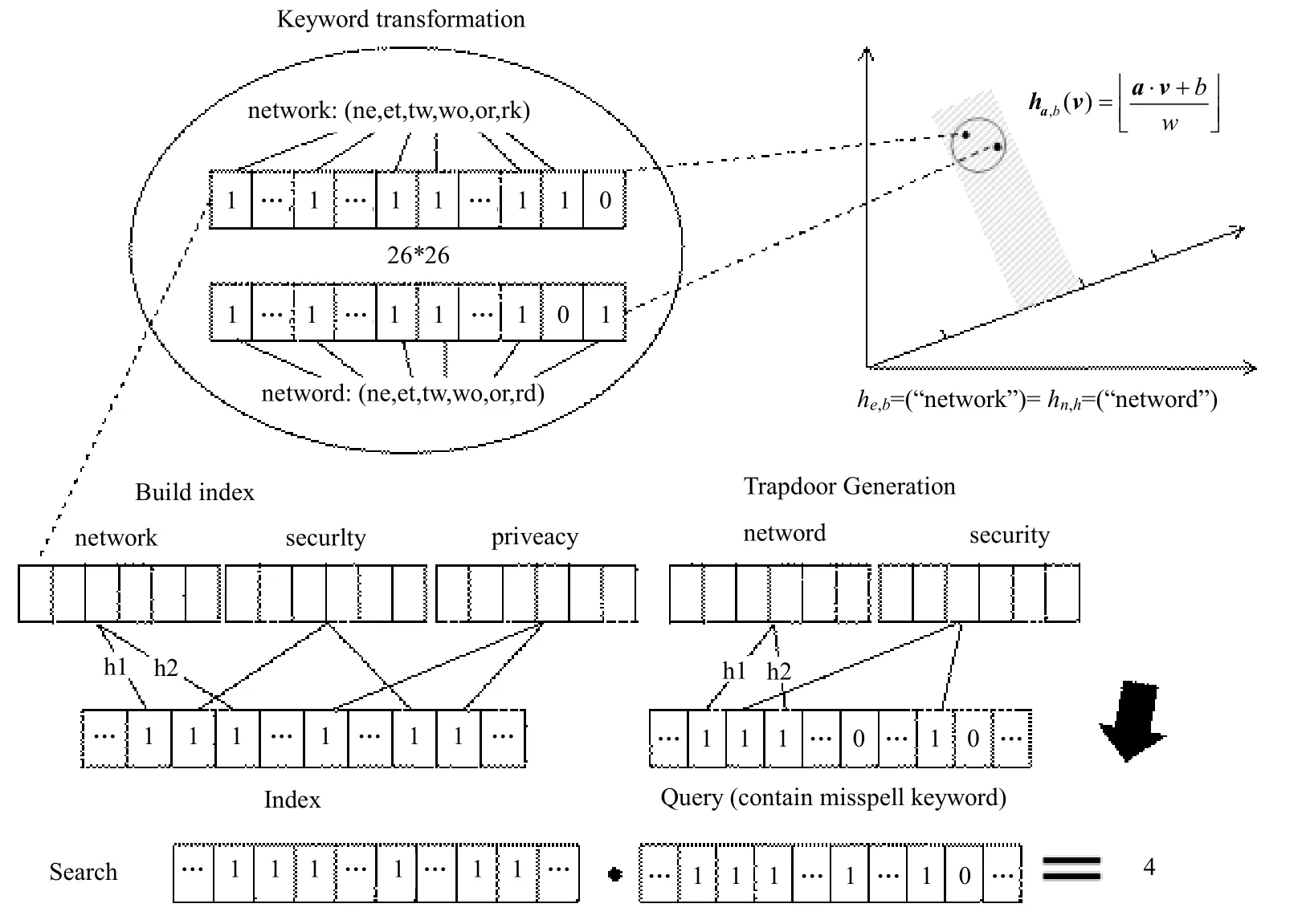
图2 查询关键词被映射到与精确关键词相同领域示意图

2.3.3 检索匹配

文件的安全索引是在一个包含了所有关键词的布隆过滤器实现的。在布隆过滤器中，关键词都被转换成双音节向量的形式，然后利用LSH函数插入到布隆过滤器的相应位置中。PEFRA-LSH算法是通过索引向量和查询向量的内积来完成检索过程的。如果一个文件中包含了一个查询关键词，那么索引向量和查询向量中对应的位应该都是1。

2.4 算法描述

PEFRA-LSH算法是由以下9个小算法组成：

1)Init(1k)：生成公共参数。具体过程如下：

① KMS将安全参数1k作为输入，输出循环群G，包括一个生成元g，一个素数q，一个哈希函数f。

② 从Zq*中选取一个随机数x，计算出h=gx。

③ 将 PK=(G,g,q,h,f)作为公钥输出，将MSK=x作为根密钥。

2)KenGen(MSK,i)：KMS执行该算法生成用户密钥Kui和服务器密钥Ksi。具体过程如下：

① 对于用户i，KMS从Zq*中随机选择一个数xi1，然后计算xi2=x-xi1。

② 将xi1作为输入，输出SK=(M1,M2,S)，其中M1，M2∈Rm×m为可逆矩阵，S∈{0,1}m是一个向量。

③ KMS将用户密钥Kui=(xi1, SK)发给用户i，服务器密钥Ksi=(i,xi2)发给服务器。服务器收到Ksi后，更新存在其上的用户-密钥映射关系Ks=Ks∪(i,xi2)。

3)IndexBuild：用户执行该算法建立文件的索引ID。具体过程如下：

① 从p-stableLSH函数群H={h:{0,1}26×26→{0,1}m}中选取l个独立的LSH函数。

② 从文件D中抽取出关键词的集合WD={w1,w2,…,wn}，其中wi∈{0,1}26×26。

③ 对于关键词wi，使用LSH函数hj∈H将关键词插入到布隆过滤器ID中构成索引。

4)U-Enc(xi1, filei,ID)： 用户执行该算法加密数据。具体过程如下：

① 加密文件：利用ElGamal代理加密算法加密文件为C(filei)=(gx,grxi1filei)。其中r是从Zq*中随机选择的一个随机数，filei∈File。

② 加密索引：xi1是用户i的私钥，它可以生成另外的一个密钥KI以及使用SK来加密索引。

③ 通过哈希函数f产生密钥KI=f(xi1)。

④ 将索引文件ID按如下规则划分为两个向量{I′，I′}：对于每个元素ij∈ID，如果Sj∈S且Sj等于 1，则设置ij′=ij′′=ij；否则ij′=1/2×ij+r，ij′=1/2×ij-r，其中r为随机数。

⑤ 加密索引文件ID：EncSK(ID)={M1TI′，M2TI′′，Enc(KI,fidw)}，其中Enc可通过AES或DES实现。

⑥ 将文件C(filei)与索引EncSK(ID)传给服务器。

5)P-Enc(i,xi2,C(filei))：服务器收到加密的文件与索引后，会执行该算法对文件进行再次加密。具体过程如下：找到与用户i对应的服务器密钥xi2，计算(gr)xi2*grxi1filei=grxfilei，最终加密后的密文C*(filei)=(gx,grxfilei)filei∈File。

6)Trapdoor(Q)：用户j想要用关键词搜索相关加密文件，需用该算法产生一个陷门。过程如下：

① 首先为查询Q生成一个m位的布隆过滤器，对于每个查询关键词qi∈Q，使用相同的l个 LSH函数将查询关键词插入到布隆过滤器中。

② 将查询Q按相同规则划分为两部分向量如果Sj∈S且Sj等于 0，则设置否则其中r′为随机数。

④ 用户将EncSK(Q)发送给服务器。

7)Search：服务器利用该算法寻找相关的加密文件。具体过程为：服务器接收到用户的陷门EncSK(Q)后，用EncSK(Q)与加密索引EncSK(ID)进行内积运算，输出结果为如果运算值与原索引和查询内积运算的值相同，即则关键词匹配成功，返回满足条件的加密后的文件号Enc(KI,fidw)，服务器对Enc(KI, fidw)解密后得到fidw，即得到相关的加密文件C*(filei)。

8)P-Dec(j,Ksj,C*(filei))：解密部分密文。具体过程为：找到存储在服务器的用户j对应的服务器密钥Ksj=xj2，利用xj2对C*(filei)进行部分解密。计算grxfilei*(gr)-xj2=g(x-xj2)rfilei=grxj1filei，因此密文变成C′(filei)=(gr,grxj1filei)。服务器将C′(filei)发给用户j。

9)U-Dec(xj1,C′(filei))：用户执行该算法获得最终明文文件。具体过程为：用户j收到服务器发来的密文C′(filei)后，利用密钥xj1去计算grxj1filei*(gr)-xj1=filei，进而解密该加密文件，得到最终明文文件。

3 算法安全性分析

定义 1 定义History为用户提交的文件集合Δ，由Δ构造而成的索引集合I以及查询关键词集合W=(w1,w2,…,wk)，表示为H=(Δ,I,Wk)。

定义 2 定义View为H在私钥sk加密下的密文形式，表示为V(H)，V(H)包括加密文件Encsk(Δ)，加密索引Encsk(I(Δ))以及陷门Encsk(Wk)。V(H)是云服务器能够看到的信息。

定义 3 History痕迹记为Tr(H)，即被服务器获取的一些信息，包括存取模式以及搜索结果。Tr(H)其实是一组查询关键词集合，Tr(H)={Tr(w1),Tr(w2),…,Tr(wk)}以及Tr(wi)={(δj,sj)wi⊂δj,1≤j≤|Δ|}，其中sj表示查询关键词wi与文件δj之间的相似度。

定理 1 基于局部敏感哈希的模糊检索算法(PEFRA-LSH)在已知密文模型下是安全的。

给定两个具有相同痕迹的history，如果云服务器不能区分它们中的哪一个是由模拟器生成的，那么云服务器就不能从搜索结果及存取模型中获取索引和数据集的相关信息，说明算法是安全的。

证明：设S是一个模拟器，能模拟出一个云服务器不能区分的View，V(Encsk(Δ),I,T(Wk))。步骤如下：

1)S选择一个随机的δi′∈{0,1}|δi|,δi∈Δ，1≤i≤|Δ|，输出Δ′={δi′,1≤i≤|Δ′|}。

2)S随机选取两个可逆矩阵M1′，M2′∈Rm*m，一个向量S′∈{0,1}m，然后令sk′={M1′,M2′,S′}。

3)对于每一个wi∈Wk，1≤i≤k，S按照以下步骤构造出Wk′和陷门Encsk′(Wk′)：

① 生成查询关键词wi′∈{0,1}m。生成过程中要确保查询关键词wi′中1s的数目和原查询关键词wi中1s的数目相同，但是位置不同。输出W′={wi′,1≤i≤k}。

②为每一个查询关键词wi′生成陷门Encsk′(wi′)，输出Encsk′(Wk′)={Encsk′(w1′), Encsk′(w2′),…,Encsk′(wk′)}。

4)为生成I(Δ′)，S先为每个δi′∈Δ′生成一个m位的空向量作为索引，表示为Iδi′。然后执行以下步骤：

① 对于每个wi∈Wk，如果wi⊂δj，那么S将Iδj′置为Iδj′+ wi′，1≤j≤|Δ|。

②S通过将{0,1}m中比1大的元素替换为1的方法，将每个Iδj′转换成一个向量，其中1≤j≤|Δ′|。

③S生 成 Encsk′(I(Δ′))=Encsk′({Iδj′}，1 ≤j≤|Δ′|)。

5)最后，S输出V′=(Δ′, Encsk′(I(Δ′)),Encsk′(Wk′))。

由于加密索引Encsk′(I(Δ′))和陷门Encsk′(Wk′)产生的痕迹与云服务器获取的加密索引和陷门产生的痕迹是相同的，则称不存在一种概率多项式P.P.T能够区分模拟器生成的ViewV′和原来的ViewV(H)。由于对称加密的语义安全性，没有一种概率多项式P.P.T能够区分出Encsk(Δ)和Δ′。索引和陷门的不可分辨性建立在安全KNN加密和分裂过程中引入的随机数的不可分辨性的基础上。因此，云服务器在已知密文模型下不能获取相关信息，这就证明了本文PEFRA-LSH算法在已知密文模型下是安全的。

证毕。

4 实验结果与分析

4.1 实验环境设置

实验在一个基于Openstack的云计算平台上完成。该平台部署在由20台服务器构成的服务器集群上，并利用虚拟化技术创建多台KVM虚拟机，通过Swift存储策略共同达到更真实的云环境。实验随机选取多个文件作为数据集，文件中的关键词总数目多达5 734个，每个文件中的平均关键词数为147个，最少关键词数为112个，最大的为175个。实验时采用一个2-stable 局部敏感LSH函数建立索引和查询。

实验内容有：测试本文算法在不同数目关键词情况下加密时间和检索时间；将本文算法与基于字典的模糊搜索加密算法(DFSC)[13]在加解密时间、加密后的密文长度、关键词的检索时间进行比较。DFSC算法同样支持加密关键词的模糊检索。

4.2 算法的加密时间和检索时间实验

4.2.1 索引生成时间和查询陷门生成时间实验

本文PEFRA-LSH算法的索引生成过程主要包括布隆过滤器生成和加密运算。布隆过滤器生成过程的时间耗费来自于哈希函数的计算。查询陷门的生成过程与索引生成过程一样，不同的是查询陷门允许关键词拼写有错误。实验中随机选取1～20个不同关键词进行多次测试实验，取平均值。索引生成时间和查询陷门生成时间的实验结果如图3和图4所示。从图中可以看出，PEFRA-LSH算法的索引生成时间和查询陷门生成时间都随着关键词数目的增加而增加，且这两个时间的数值非常接近，相差不大。这是因为生成陷门和生成索引的步骤是一样的，只是关键词拼写不太一致，导致生成时间有一些小的差别。

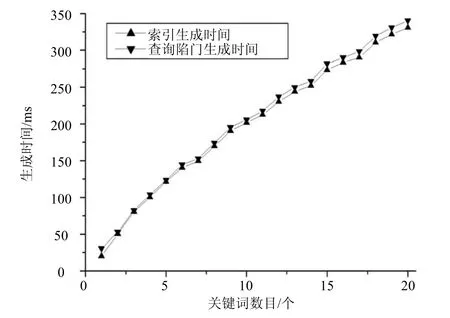
图3 不同数目关键词的索引生成时间和查询陷门生成时间

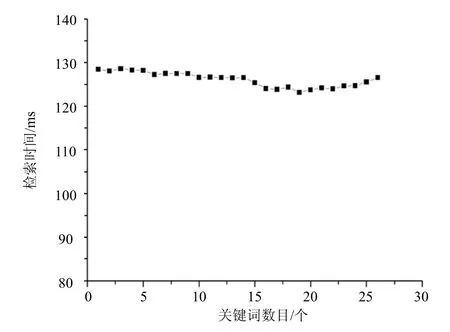
图4 不同数目关键词的检索时间

4.2.2 检索时间实验

PEFRA-LSH算法的检索时间主要取决于算法内积匹配的运算时间。实验随机选取了1～26个不同数目的关键词进行测试，多次实验取平均值。实验的结果如图5所示。从图中可以看出，PEFRA-LSH算法的索引时间没有随着关键词数目的增加而有大幅度的变化，而是处于一种相对稳定的状态。

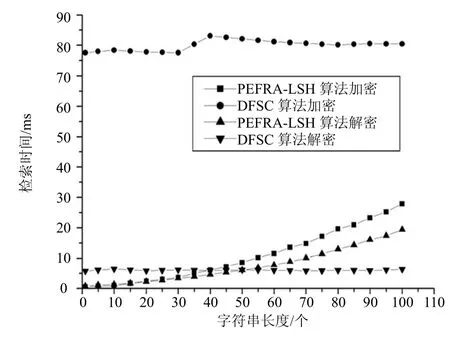
图5 两个算法的加密和解密性能对比(平均时间)

4.3 对比实验

4.3.1 加解密性能对比

加解密性能对比实验是对不同长度的字符串进行加解密操作，比较本文算法和DFSC算法的加解密性能和加密后生成密文的长度。不同长度字符串的加密和解密性能实验结果如图5所示，生成密文长度的实验结果如图6所示。从图中可看出，本文算法加解密时间随着字符串长度增加而增大，DFSC算法加解密时间并没有随着字符串长度增加而有明显增长；本文算法密文字符串长度与明文字符串长度呈线性增加，DFSC算法密文字符串长度不变。对比实验结果说明，本文算法的加密性能明显比DFSC算法好；在字符串长度为40个字符之前，本文算法的检索时间少于DFSC算法，但是当字符串长度超过50个字符以后，本文算法的检索时间大于DFSC算法。

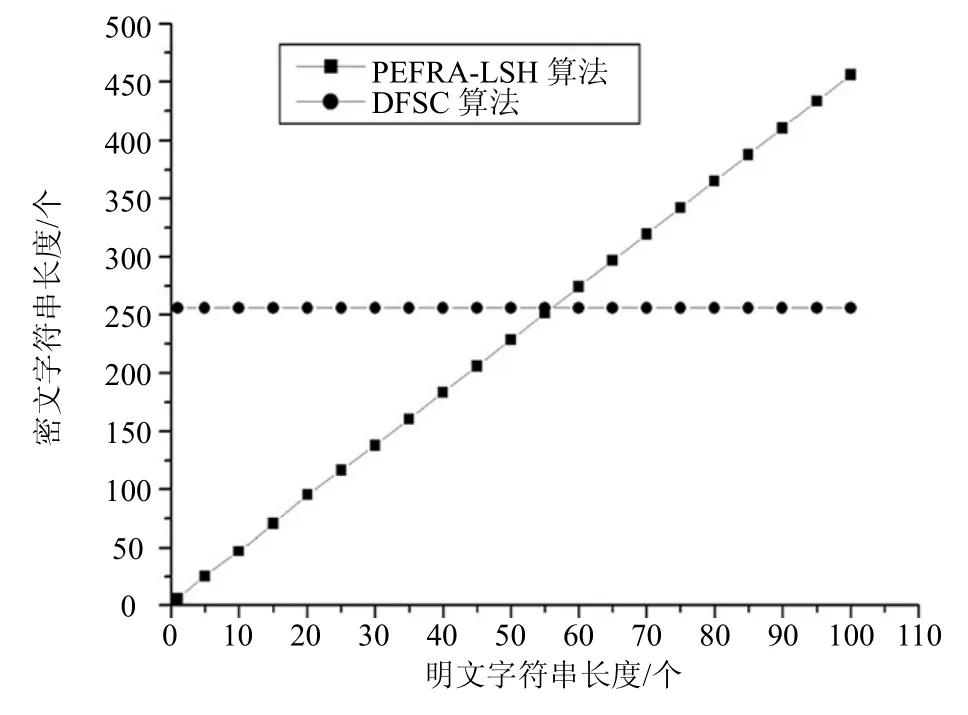
图6 两个算法加密后生成的密文长度对比

4.3.2 检索时间对比

检索时间对比主要是评估本文PEFRA-LSH算法与DFSC算法在相同编辑距离d时，对于长度不同的关键词进行检索所需时间。实验结果如图7和图8所示。从图中可以看出，在编辑距离相同情况下，本文算法的检索时间随着关键词长度的增加和编辑距离增大而增加，而DFSC算法的检索时间变化不大。当编辑距离增大时，本文算法的检索时间随着关键词个数的增加显著增大，明显大于DFSC算法。这说明DFSC算法的检索时间性能优于本文算法。

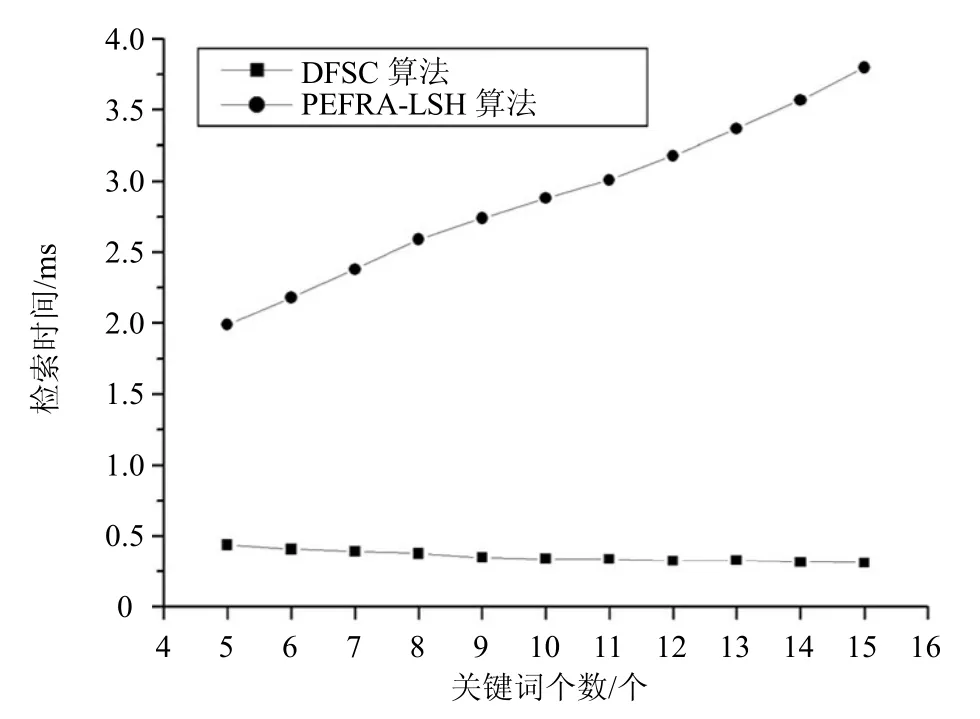
图7 相同编辑距离下两个算法的平均检索时间比较(d=1)

图8 在相同编辑距离下两个算法的平均检索时间比较(d=2)

5 结束语

针对现有的多用户可搜索加密方案和模糊加密检索机制存在的问题，本文提出了一种基于局部敏感哈希技术的代理模糊检索加密算法。该算法支持多个关键词的模糊检索以及文件由多个授权用户共享加密文件，通过LSH函数以及内积运算，将关键词插入到布隆过滤器中，并构建文件索引，使得算法不必预先构建模糊关键词集，能高效地查找到与关键词相关的文件，存储开销较小。但是应该指出的是，本文算法的检索时间明显大于DFSC算法，这也是本文算法需要进一步改进的地方。