一种基于检测器数据的交叉口交通运行特性研究方法

赵远洋，薛运强，徐佳云，刘 锐

（华东交通大学交通运输与物流学院，江西 南昌 330013）

0 引言

近年来，传感器技术蓬勃发展。特别是在交通运输领域，以道路检测器为例，其可靠性得到了大幅度提升，并且所采集的数据量很大，便于后续进行研究分析。目前，检测器数据在交通运输领域的应用大体上有以下几类：一是基于一些算法（如小波分析、神经网络、聚类算法等）进行交通预测[1]；二是关于道路交通参数的综合研究[2]；三是通过分析其自身的检测属性进而优化检测器进行物理布局[3−4]。当前数据挖掘算法应用广泛，而且与传统的时间序列算法相结合更有意义。特别是对于交叉口，由于其存在4个方向，各个方向之间的联系十分紧密，仅根据交通流的时间分布及空间分布来研究其交通运行特性是不够全面的。国内有很多关于交叉口交通运行特性的研究，其中按交通流组成成分划分，一类是以机动车为研究主体，讨论交叉口的运行指标[5]；另一类是以非机动车和行人作为研究整体，研究慢行交通对交叉口通行效率的影响等[6−7]。国外的一些研究还倾向于说明交通参与者的行为对交通运行特性的影响[8−9]。

为了更加全面地对道路交通运行特性进行研究分析，本文结合江西省南昌市青山湖区某交叉口的交通数据，按短期、中期、较长期3个阶段分解交通流量，提出一种组合式交通流量特征研究方法，该方法不是简单地将交通流数据与某种数学算法结合而得出整体的流量特征，而是利用交通流数据本身所具有的状态相似性和周期性，采用谱聚类算法与快速独立成分分析（Fast Independent Component Analysis，简称FastICA）算法分阶段分析，并比较各进口流量特征，最后得出研究结论。该研究结论可为交通管理部门制定更加有效的交通控制措施提供科学依据。

1 研究方法

1.1 谱聚类

短期交通流量分布的随机性较大，为了降低其对结果准确度的影响，采用以几何理论为背景的谱聚类算法。在谱聚类[10−12]算法中，能够根据数据集合构造出一个描述各数据点相似度的矩阵，并且计算矩阵的特征向量和特征值，然后选择恰当的特征向量对不同的数据点聚类。本文在处理全天流量数据时，应用谱聚类算法，其具体实现步骤如下[13−16]：

（1）汇总各进口道的流量数据，共分为4个进口道，每个数据单元代表每5min流量数据，最终制作成288×4矩阵；

（2）先后对南北进向、东西进向分别利用K近邻（K−Nearest Neighbors，简称KNN）方法将空间数据集转化为K近邻网络（即构建样本的相似矩阵S）；

（3）根据相似矩阵S构建邻接矩阵W和度矩阵D；

（4）计算拉普拉斯矩阵：

（5）构造标准化后的拉普拉斯矩阵：

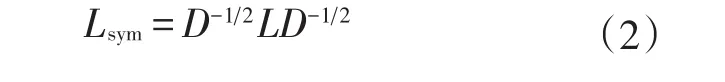
（6）计算Lsym降序的前K个特征值所各自对应的特征向量f，其中K是期望的簇数；

（7）将特征向量f组成的矩阵按行进行标准化，形成特征矩阵F；

（8）将F中的每一行作为一个样本，应用K均值（K−Means）聚类方法聚类。

1.2 FastICA算法

交通流量变化在较长时间内会呈现出一定的规律性，而信号波形的变化往往呈一定的周期性，将交叉口交通流量变化与信号变化相类比，发现它们在时间上具有一定的相似性，由此为了减少无关因素对较长期流量数据变化特征的影响，引入FastI⁃CA算法。FastICA算法是独立成分分析（Indepen⁃dent Component Analysis，简称ICA）算法中适用范围广泛、分离准确度较高的算法，它是基于定点递推算法得到的。将其运用至本文中，核心步骤如下。

定义信号源S(t)、混合矩阵A、观察信号X(t)、解混矩阵WT。其中ICA 关系模型为[17−18]：

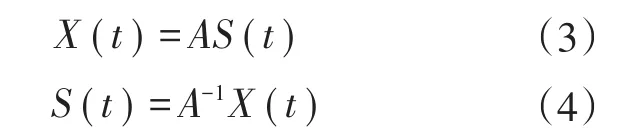
令y=WTX(t)，则y=WTAS(t)，由此可知y是S(t)的线性组合。当WT接近A−1时：

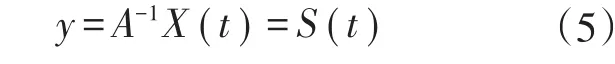
这样将问题转化为最大化y的非高斯性进而求解W。具体的算法实现步骤见图1[19−21]。其中，数据集是依据1周的流量数据建立大小为2016×4的矩阵。

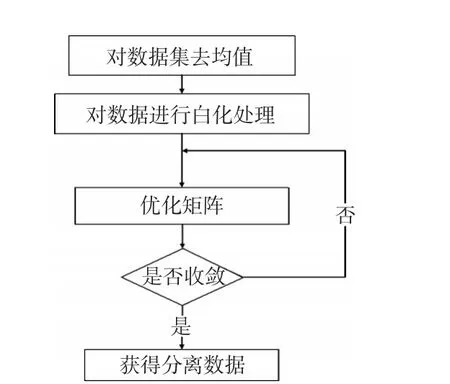
图1 FastICA算法流程图

3 算例分析

3.1 区域简介

算例交叉口位于江西省南昌市青山湖区（见图2），其中东进口与八一桥直接相连，满足往来车辆及行人的过江交通需求；西进口与庐山南大道地铁站（地铁一号线的停靠站之一）相连，南进口方向可直通红谷滩新区，北进口方向可达英雄大桥。此交叉口交通地位十分重要。

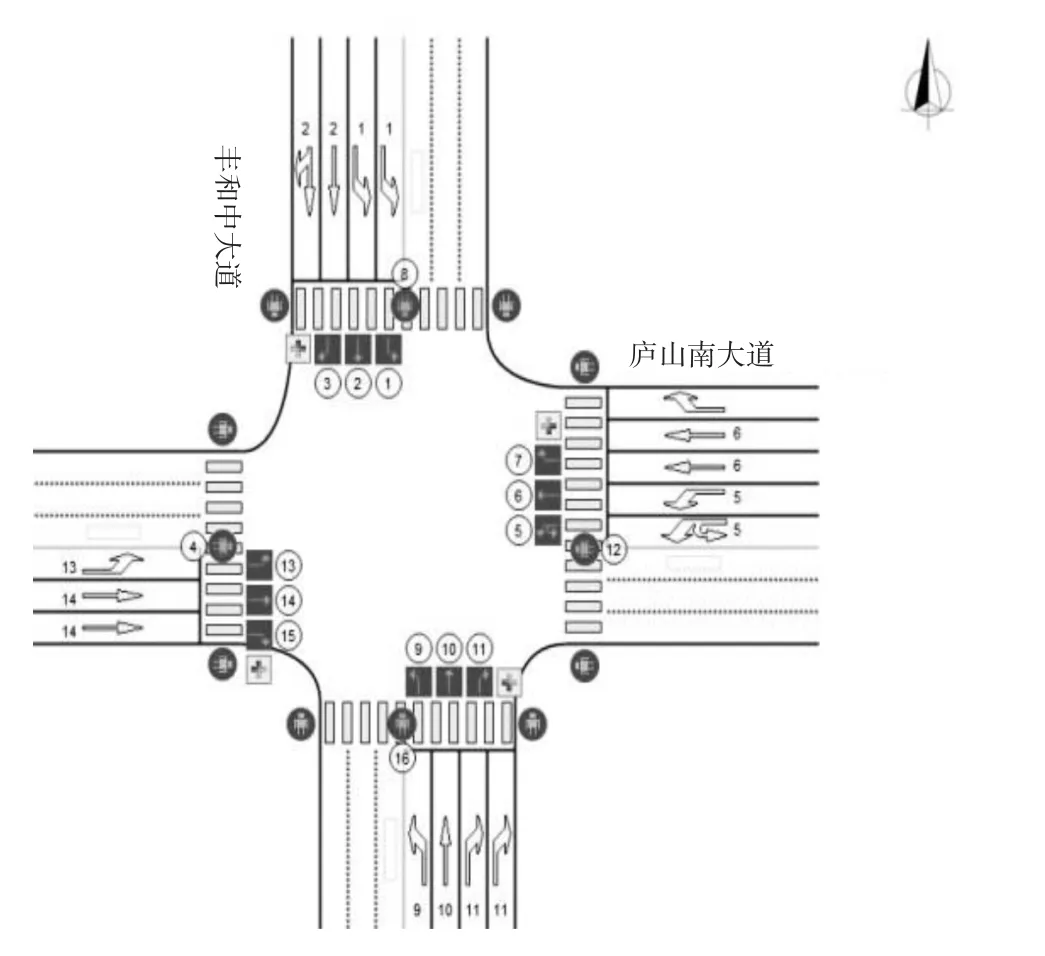
图2 交叉口平面图

3.2 数据简介及划分

选取该交叉口现有的9个车辆检测器的检测数据作为研究对象，时间为2017年10月9日—2017年10月15日（5个工作日加2个休息日），数据采样间隔为5min。为了方便研究各进口道的交通运行特性，将数据划分为4个单元（东、南、西、北）并经汇总处理后，最终得到8 064个研究数据。根据交通量的时间分布特点分别选取1h,1d,1周的数据（见图3）。

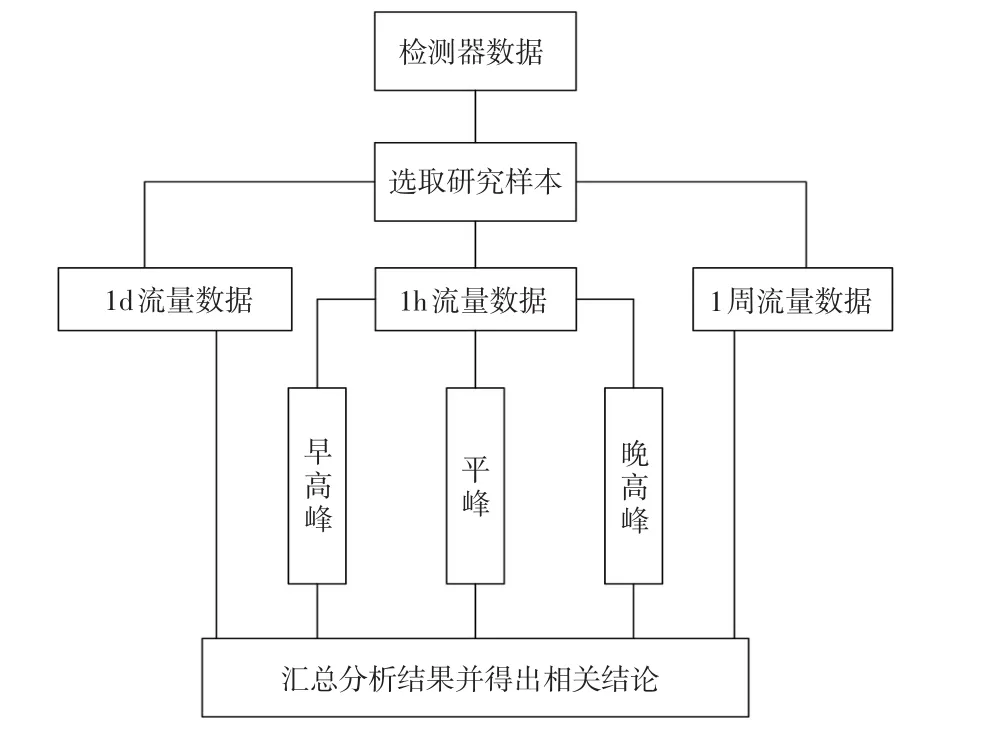
图3 检测器数据划分图

3.3 数据处理及分析

（1）关于短时交通流量的研究，分别选取2017年10月10日的早高峰小时、平峰小时、晚高峰小时的流量数据，得到了流量的方向分布（见图4）和对应的变化细节（见图5）。从图4看出，东进口的交通量不论是在高峰期还是在平峰期均维持在较高的水平，其他3个方向的流量占比较小。由此可知，在1d中的3个特殊小时时段内，八一桥对该交叉口交通运行状态的影响程度基本相同。从图5可知3个特殊时段各进口的流量变化情况，西进口的流量变化幅度比其他3个进向大，虽然东进口的流量一直居高不下，但流量的变化幅度较小。南北进口的流量变化幅度不大。以上的分析是基于3个特殊小时流量数据，属于短期研究阶段。

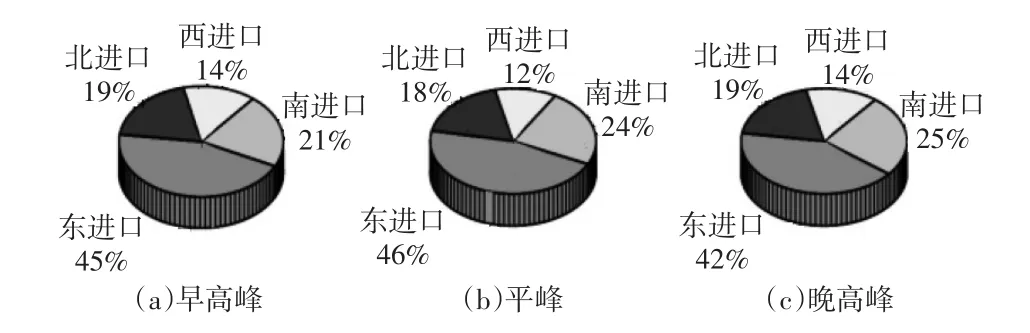
图4 小时流量方向分布图

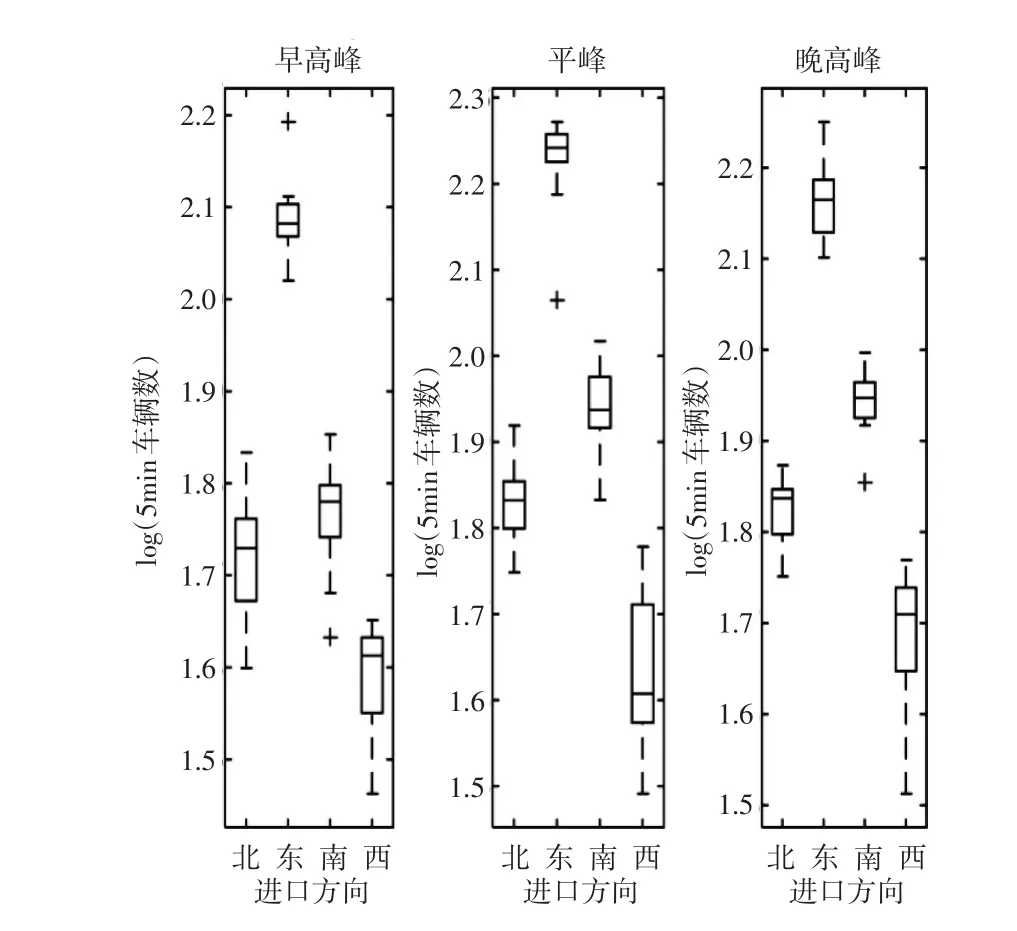
图5 小时流量变化箱线图

（2）为了更好地研究对向交通流量实时变化情况，延长检测器数据的观测时间，选取2017年10月10日全天的各进口每5min流量数据，并进行归一化处理，然后分别对东、西进口和南、北进口应用谱聚类分析法分析，最终得出了数据集的相似度图（见图6）。从图6（a）和图6（b）中可以看出，每个网络均可以被虚线较为清晰地划分为两个子图。按照对交叉口流量分析的基本主观判断，分类数（即K值）应该至少取2，存在高峰和平峰两个基本特征流量类。这里也分别计算出了其他聚类数所对应的轮廓值（见表1）。但发现不论是东、西进口，还是南、北进口流量聚类的轮廓图，K=2都比其他聚类结果要好（即K=2比其他聚类数目所得出的结果准确度更高）。这说明该交叉口高峰期与平峰期的流量特征存在较大差异。根据聚类数为2时交通量聚类分析（见图7）及轮廓图（见图8），对各类进行研究。

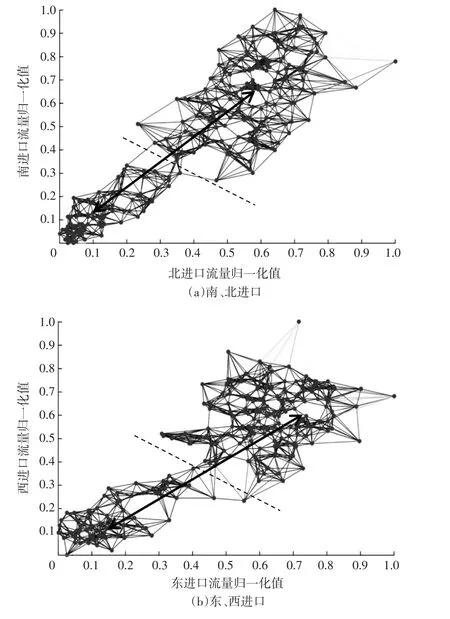
图6 相似度图

表1 对向交通量聚类效果轮廓值表

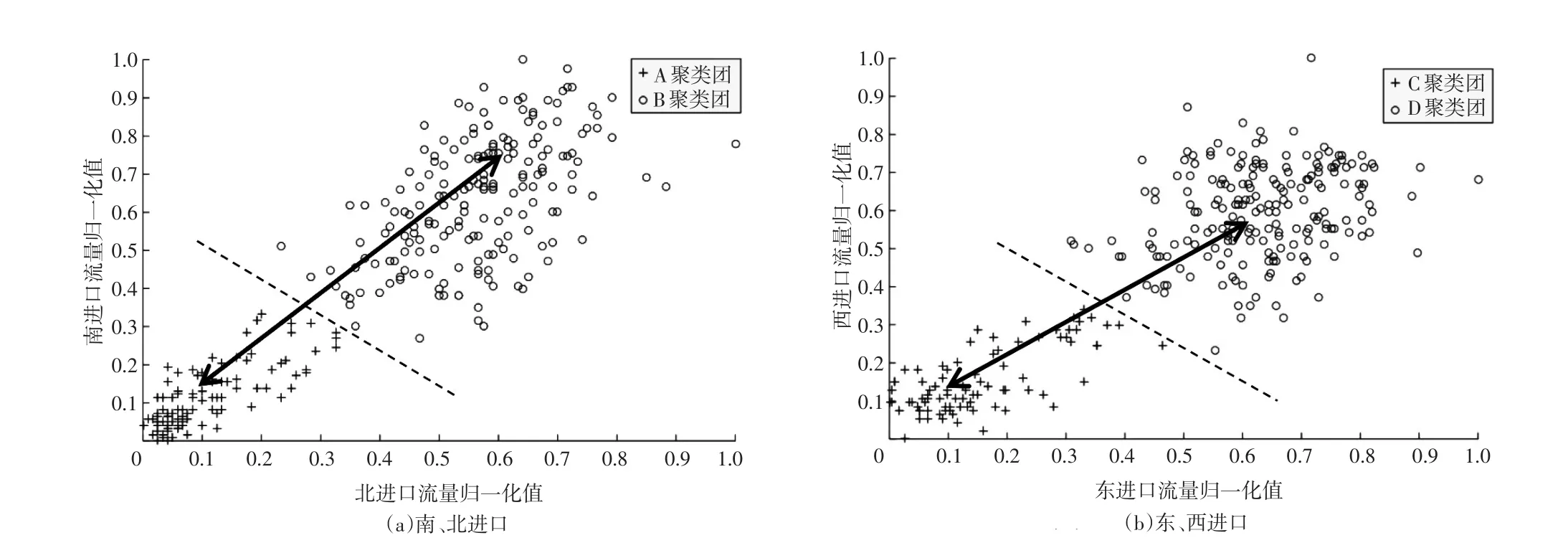
图7 交通量聚类分析（K=2）

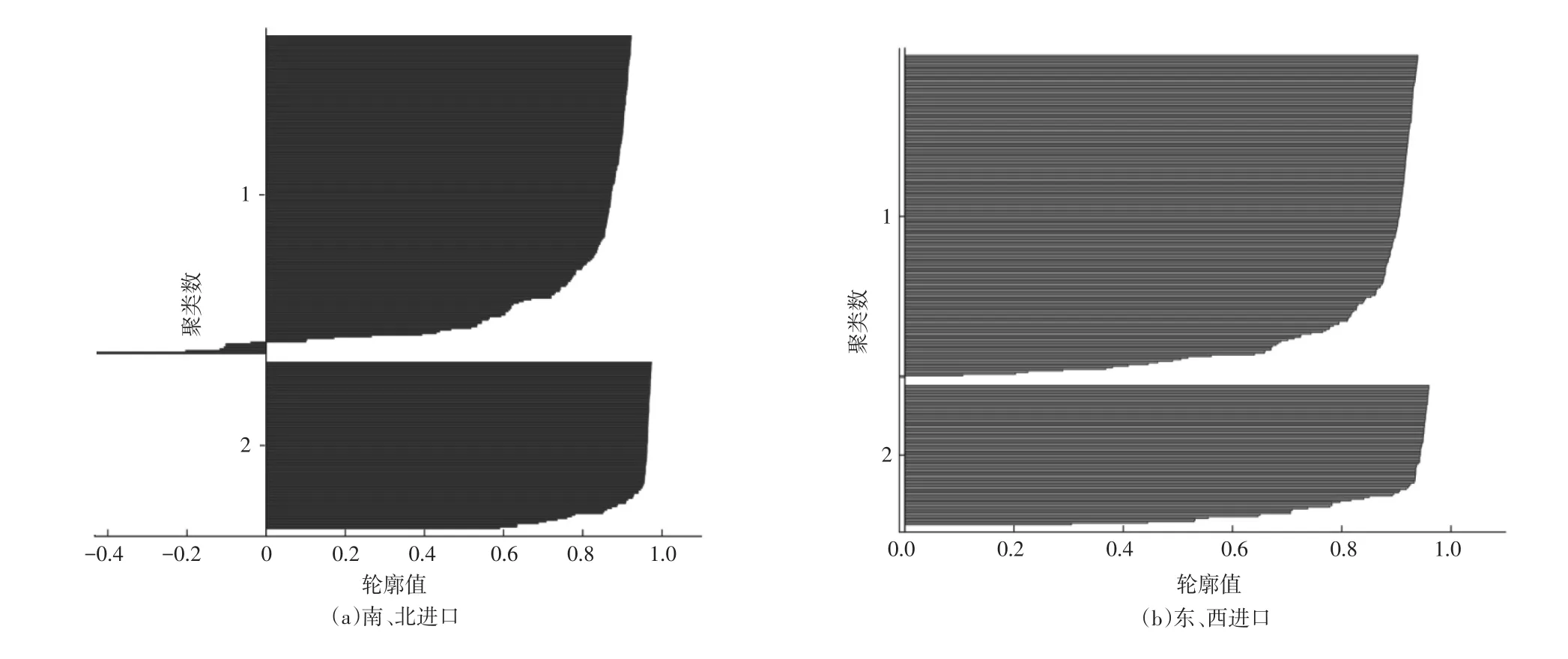
图8 交通量聚类分析轮廓图（K=2）

通过表1、图7（a）和图7（b）可知，它们各自聚类中心连线的斜率基本趋近于1，由于聚类数据是取同一时刻相同时间长度（5min）各进口道的交通量，反映了南、北两个方向车辆到达的相对情况（东、西方向同理）。从南、北两个方向聚类流量点的分布可以看出，车辆在南进口到达数比北进口多。在A聚类团与B聚类团分界处（图中虚线）流量点排列较为规整，即两个方向相似的车辆到达情况比较多。在图的左下角，存在分布集中的流量点，表明两个进口道在观测日中存在一段时间车辆到达率很低的情况。从东、西两个方向聚类团流量点的分布可以看出，由于存在东进口车流量的客观影响，使聚类中心连线偏下，然而分界线周围流量点分布稀疏，即两个方向车辆到达数差异较大。虽然东进口车辆到达数要大于西进口，但西进口车辆到达随机性更大，最终造成D聚类团纵向离散程度高。

（3）针对交通流量的时间变化情况，为挖掘各进向交通流量影响规律，选取2017年10月9日—2017年10月15日1周的流量数据，进行方向分类得到图9。根据图9中数据趋势的变化，各进向流量分布特征和日变化特征相似，平均流量曲面基本上呈现出了该时间尺度下流量的分布情况。东进口仍然是这个交叉口主要的流量输入方向。西进口短时流量变化幅度减弱，与其他进口间的流量相比要更稳定。对各进口流量利用FastICA算法进行降噪处理，分别得到处理前（见图10（a））及处理后（见图10（b））变化规律。在相同的描述范围内，各向流量的变化特征更为明显，存在一定的变化规律。比如，北进口流量变化趋势明显，而其他3个方向所呈现的变化趋势比较模糊，并且西进口流量变化情况与短期流量变化情况相似，短期流量较大的东进口呈现出较西进口更为稳定的流量分布。

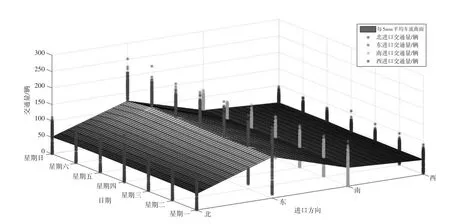
图9 交叉口各进口5min交通流量统计图（2017年10月9日—2017年10月15日）

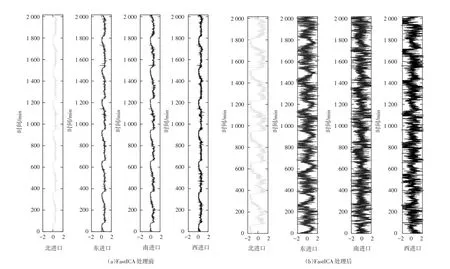
图10 1周内交叉口各进向流量变化图

4 结语

综合上述分析，可得出如下结论：从宏观角度看，本文所提方法融入了信号降噪算法，浓缩并提炼了数据的周期性特征，可以较好地把握交叉口各进口流量的长期变化趋势；从微观角度看，该方法应用谱聚类算法，通过分析数据的几何相似性特征，能够避免短期流量突变而造成的结果失真，对保证研究结果准确性具有十分重要的意义。算例的分析过程表明，该方法在理论计算上实现了多个时间角度的参照对比，使得结果更具代表性。最后，本文所提出的方法在理论上能够得出交叉口交通运行特征，为后续提高交叉口通行效率的研究奠定了理论基础。由于该方法应用的数据集较小，造成时间长度的上限是1周，该时间单位对交叉口长期交通运行特性的把握还不够全面，所以扩大数据集和时间长度是下一步研究的重点。