面向通风需求的涡簧储能系统设计及运行方式分析

冯 可 袁艳平

（西南交通大学机械工程学院 成都 610031）

0 引言

随着传统能源消耗与污染的日益严重，如何对能源进行收集以及存储显得尤为重要。在日常生活中，机械能普遍存在，按照一般定义机械能包括动能、重力势能、弹性势能，而以上三种能量中弹性势能通常以弹性形变的形式存储在弹性元件中，当弹性元件恢复形变的同时也即弹性势能的释放，从而可实现能量在时间和空间上的转移和转换，实现能量的供求平衡，且具有低成本、高储能密度、可重复利用等特点[1-3]。因此弹性储能、释能特性以及储能系统进行的相关研究具有重要意义。

弹簧的种类多种多样，按其形状可分为螺旋弹簧、蝶形弹簧、环形弹簧、盘簧和板弹簧，按其受力性质可分为拉伸弹簧、压缩弹簧、扭转弹簧和弯曲弹簧等[4]。单独针对弹簧，一些学者对其在储存能量以及释放能量过程中表现出来的固有特性进行了研究，其中Tang等[5]人阐述了基于螺旋弹簧的机械弹性储能技术的基本概念，并建立了三种形式的螺旋弹簧的有限元模型，包括两种不同尺寸的矩形截面螺旋弹簧和一种特殊截面螺旋弹簧，研究结果可为结构设计和动力学分析提供参考。在此基础上，Muñoz-Guijosa[6]建立了广义平面涡卷弹簧模型，研究了不同设计参数对弹簧性能的影响，分析了沿着涡卷弹簧长度，例如涡簧钢带厚度、曲率，以及其与涡簧盒直径和芯轴直径之间的关系，最终研究结果表明随着涡簧材料的弯曲刚度减小或者涡簧钢带自由长度的增加，在同一扭矩作用下，涡簧绕芯轴的旋转角度将减小。此外模型和测试结果均显示涡簧钢带厚度是影响涡簧特性曲线（扭矩-挠度）的重要参数。

此外，在弹性储能系统方面，就输入输出能量方式而言，常用的为随机不稳定性输入、可控输出[7]，譬如Tang等[5]提出的用于风力发电的机械弹性储能系统。该系统一方面可以有效地抑制风电功率波动，使输出电压更加平滑，另一方面还可以提高电能质量。其原理为：当电网电能溢出时，电网电能带动双馈电机工作，双馈电机此时处于电动机状态，从而驱动平面涡卷弹簧卷紧开始将过剩的电能以弹性势能形式储存起来，当电网电量不足时，控制系统控制平面涡卷弹簧松开开始释放能量，从而驱动双馈电机发电，实现能量在时间上的转移，使能量达到供求平衡。此外，波浪能作为一种同样具有种随机不稳定特性的新型能源，如对其进行收集存储成为众多学者的研究对象[8-11]，譬如宋洪侠等[8]设计了一种摆动式机械俘能装置，该装置通过摆锤、涡簧等机构实现对波浪能量的收集，并通过转换机构驱动发电机产生稳定的电能。

综上所述，目前大型弹性储能系统主要针对新型能源的收集，譬如风能、海浪能等。此外，储存的弹性势能以电能形式输出，而很少直接以机械能形式输出，故本文以重力势能为储能对象，以平面涡卷弹簧（简称“涡簧”）为储能原件，以通风（排烟）机为负载，采用纯机械式的能量输出方式，中间无机械能-电能的二次转化，设计储能装置并进行优化，且将该装置用于地下车库升降机械下降过程中重力势能存储，并建立该储能系统数学模型，求解输入输出物理参数，譬如储能量、储能效率、输出功率等，为大型弹性储能系统设计运行提供参考。

1 涡簧储能装置介绍

1.1 涡簧储能装置结构介绍

以平面涡卷弹簧为核心储能原件，设计出能实现快速储能和释能的机械储能装置，该装置主要由驱动系统、输入传动系统、扭簧拧紧机构、输出系统以及控制系统组成，其原理如图1[12]所示。

图1 储能装置原理图Fig.1 The schematic of energy storage device

将储能装置原理图中储能过程中所用齿轮的转动惯量J以及阻尼D等效到转盘轴上，计算可得J=3.49e-2kg·m2、D=2.7e-2N·m·s/rad[13]。 根 据 GB 9819-88《叉瓦式擒纵机构基础尺寸系列》设定摆轮周期设为1/3s，擒纵轮齿数为15齿，因此擒纵轮的转速为1/(15×(1/3))=0.2r/s，即12r/min，令涡簧轴20到摆轮游丝擒纵调速机构的传动比为ia，摆轮游丝擒纵调速机构到输出轴21的传动比为ib，输入轴到涡簧轴的传动比为i（i=0.5），则涡簧释放转速n释放为 12ia。

1.2 储能及释能过程介绍

（1）储能过程

电机5为转盘1提供初始动能，当转盘具有一定的初始动能之后，切断电机电源，进行下一步操作，即使转盘通过传动系统Ⅱ，即齿轮2、4、9、10带动涡簧拧紧机构Ⅲ工作，平面涡卷弹簧开始储存能量直至转盘速度为零，即将转盘的动能全部转为平面涡卷弹簧的弹性势能。在此过程中棘轮棘爪机构11将起到防止涡簧反转的作用，当信号采集系统监测到涡簧储存的能量达到其饱和状态时，控制系统将会切断转盘与涡簧拧紧机构间的联系，此步操作亦通过输入传动系统中的电磁离合器1实现，此外由于驱动系统中的单向轴3以及输出系统中的单向轴承13，使得在储能过程中驱动系统Ⅰ、输出系统Ⅳ与输入传动系统Ⅱ、涡簧拧紧机构Ⅲ隔离开来。

（2）释能过程

当装置需要对外界做功时，通过电磁离合器1切断转盘与涡簧拧紧机构间的联系，此外还需控制与棘轮联动的电磁离合器2使得棘轮棘爪机构脱离涡簧拧紧机构，由于单向轴承9的存在使得在释能过程中涡簧拧紧机构与输入传动系统断开，由于输出系统中擒纵调速机构的存在，则平面涡卷弹簧通过输出系统Ⅳ以恒定转速释放能量，驱动风机工作。

2 用于地下车库通风的储能系统简化模型建立及运动分析

2.1 系统简化模型的建立

如图2所示，建立升降机械储能示意图，提升储能部分为1.1节中的储能装置，升降重物质量为m，设升降重物的重量F=mg在一个升降或下落过程中为常值，提升、下落过程在垂直方向，平面涡卷弹簧储能过程为重物的下落过程，因此在此主要讨论重物的下落过程。故假定外力F外通过储能装置中的转盘将重物提升至最高点，在此过程中储能装置中的电磁离合器1处于分离状态，切断外部环境与涡簧的联系，故涡簧处于非工作状态。然后撤去外力作用，重物在自身重力作用下开始自由下落，该阶段位移为h，在某时刻控制电磁离合器1处于吸合状态，此时涡簧开始储能，储能阶段位移为H-h。建立坐标系0-x，以+x方向为下落方向，系统的落差高度为H。忽略非线性，把整个系统简化等效为线性机械动力学系统，具体为单自由度有阻尼受迫振动，将其等效为力学模型，如图3所示[14]。

图2 升降机械储能示意图Fig.2 The diagram of energy about the lifting machinery

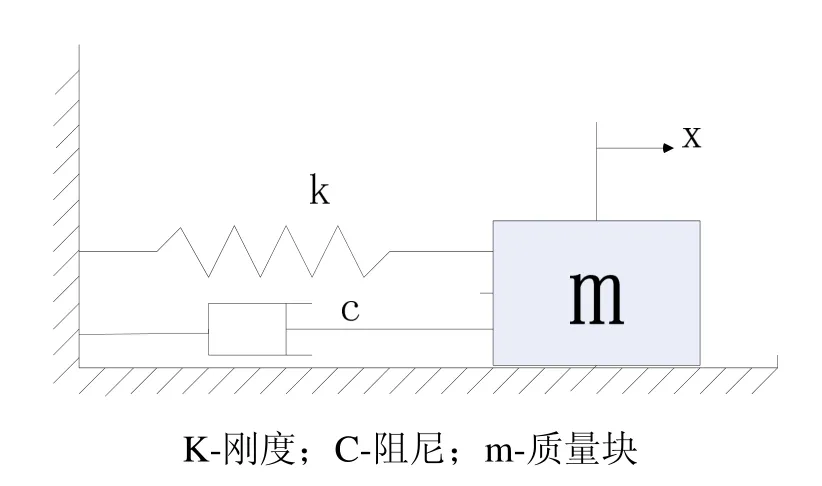
图3 等效力学模型Fig.3 Equivalent mechanical model

2.2 系统运动分析

2.2.1 储能过程自由下落阶段

自由下落阶段，是指不储能阶段，设下落距离为h，位移坐标记为x1，时间记为t1。自由下落阶段在x方向的系统运动方程为[14]：

式中：Me1为等效质量，包括了储能装置中的转盘和重物，由于绳索质量较小，故在此忽略不计；C1为等效阻尼。

2.2.2 储能过程储能阶段

储能阶段的位移坐标记为x2，时间记为t2，x2为涡簧的相对位移量，则储能阶段系统运动方程为[14]：

将式（3）代入式（2）可得：

其中令：

2.2.3 储能过程自由下落阶段与储能阶段整合分析

把自由下落阶段（可称第一阶段）和储能阶段（可称第二阶段）结合起来分析整个下落过程。自由下落阶段直至位移x1=h时具有速度（h仍为待定值）。储能阶段的初始速度为即储能阶段初始时的重物速度等于自由下落阶段末的重物速度。储能阶段的初始位移x20为储能时的已有上簧量，其值视实际情况而定：若是第一次储能，则x20等于零，若是连续的第二次储能，则x20为第一次下落的储能量，……，若是一端储能，另端释放做功的情形，则x20将为动态变化量。重物达系统底部时，实际的储能位移为要求此时速度为是为防止大的冲击而设置的速度限制值，在此假定理想情况时重物到达底部时在此针对此种情况对系统控制策略进行求解。

2.2.4 释能过程

由1.2节可知，在能量释放过程中，在摆轮游丝擒纵调速机构参数不变、涡簧无能量输入且由芯轴驱动输出能量的情况下，涡簧释放转速n释放由ia决定，风机转速由ib决定。将涡簧释能（芯轴驱动）时芯轴输出转矩T'的计算公式为：

式中，θh为涡簧现有储能角位移，其余参数意义同式（3）。

现不考虑输出传动系统中的一切能量损耗，释能过程单个涡簧输出功率计算如下：

2.3 系统相关参数的计算

现根据JB/T 7366-1994《平面涡卷弹簧设计计算》[15]选取型号为0.3×7×3200（mm）的平面涡卷弹簧为核心原件并计算其相关参数，此外根据储能装置转动惯量J、阻尼D及等效原理[14]计算储能系统相关参数如下：

K3=0.78；T2=0.1354N；θh=2π·18（涡簧处于饱和状态时）；R=0.0998m；Me1=4.07kg；Me2=4.08kg；Km=2.39e-1N/m；C1=0；C2=0.27N·s/rad；H=5.6m。

3 用于地下车库通风的储能系统运行方式求解

3.1 机械能连续单次输入

（1）自由下落阶段

在不考虑系统阻尼的情况下，根据自由下落阶段的运动方程，可知自由下落阶段的运动为加速度近似恒定的加速运动，可通过编程求得当t1=3.05s时，有

（2）储能阶段

②由分析式（2），即储能阶段运动方程可知在同一初始速度下，第二阶段总位移x2随着涡簧个数a的减小而增加。

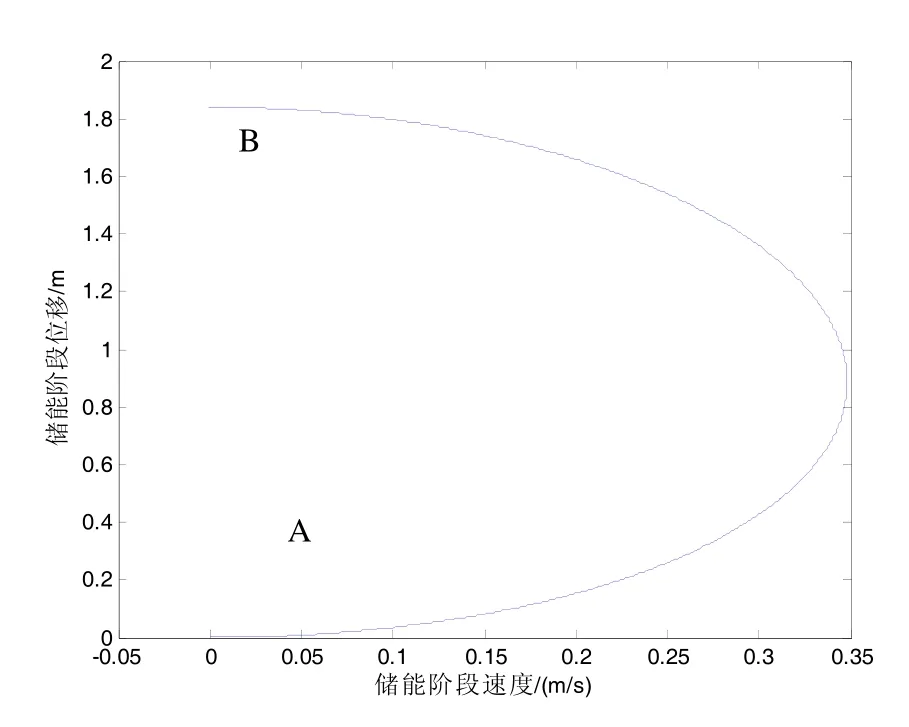
图4 储能阶段的位移-速度曲线Fig.4 Displacement-velocity curve of the stage about energy storage

（3）编程求解

根据2.2节运动分析编写程序1求解自由下落阶段位移。该程序的编写思路如下：

图5 程序1设计流程图Fig.5 Design flow chart of procedure 1

令t、T的初始值t=0.1，T=0，自由下落阶段运动方程为Me1*D2y+C1*Dy=F，该方程中的系数的物理含义以及数值同式（1），位移初始值y(0)=0，速度初始值Dy(0)=0。在x方向总位移为p，自由下落阶段末时刻速度为q；储能阶段运动方程为Me2*D2g+C2*Dg+a*Km*g=Fc，其中令Fc=F-a×(2-k3)*T2/(R*k3)。该方程中的系数的物理含义以及数值同式（4）、式（5），位移初始值g(0)=X，X为一常数，速度初始值为Dg(0)=q，末速度为gg1，每次储能阶段末在x方向的总位移为gg（此处gg以涡簧涡簧完全松弛时的自由状态为零点计数，即包含了该次储能阶段位移的初始值），程序设计流程如图5所示，其中设置abs(gg1)<0.01，abs(H-gg-p)<0.05*H，即设置两阶段位移和的相对误差在5%以内，此外介于求解时间考虑，此处设置t循环时间步长为0.01s，T循环时间步长为0.01s。

在此设定涡簧个数a=2、3、4、5，涡簧储能量随重物x方向位移变化情况如图6所示。

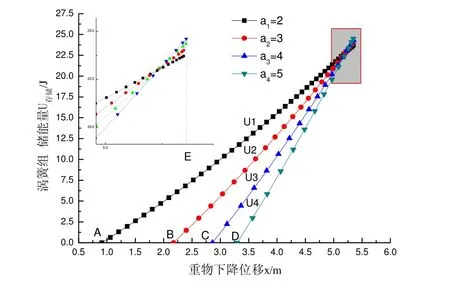
图6 储能量变化情况Fig.6 The change in energy storage

由上图可知，点 A（0.91，0）、B（2.17，0）、C（2.86，0）、D（3.30，0）为储能阶段的起始点，其纵坐标数值表示自由下落末时刻位移。由此可知随着涡簧个数增加，自由下落阶段的位移逐渐增加，且在储能阶段涡簧储能量增加速度逐渐加快，在图中表示为曲线斜率逐渐增大。此外储能阶段末时刻（E点）的储能量随着涡簧个数增加而增大，其具体数值为U1=23.72J、U2=24.00J、U3=24.38J、U4=24.64J，故其储能效率也随着涡簧个数增加而增大，分别为η1=69.51%、η2=70.33%、η3=71.45%、η4=72.21%，其原因为涡簧组刚度越大，储能过程速度变化越快，则阻力因素对系统的影响越小，回收效率越高。

3.2 机械能连续多次输入

考虑重物连续多次下落，即涡簧多次储能的情况，由2.2分析可知此种情况下，涡簧每次储能时的初始上簧量，即为上一次储能阶段末时刻的上簧量。假定下落次数为4次，即平面涡卷弹簧4次间断充能，在程序1的基础上编写程序2，可得四次下落过程中自由下落阶段的位移变换情况、平面涡卷弹簧总形变量以及相对形变量的情况。程序2设计原理见图7。

图7 程序2设计流程图Fig.7 Design flow chart of procedure 2

在重物质量m不变的情况，分析采用不用涡簧个数a对下落过程中自由下利用程序4分析涡簧个数（在此取涡簧个数为7、9、11、13、15）对下落阶段的位移、涡簧总形变量、涡簧相对形变量以及涡簧相对储能效率的影响，分别如图8、图9、图10、图11所示，此处“相对”的定义为后一次储能过程相对于前一次储能过程而言，即选择涡簧上一次储能时的末状态为下一次储能的初始状态。“总”的定义为某次储能过程相对于涡簧第一次储能时的初始状态而言。

图8 自由下落阶段的位移Fig.8 The change of displacement in the stage of free fall

由图8可知，下落阶段的位移随着涡簧个数的增加而增加，随着储能次数的增加而增加。通过定性分析每次下落过程中储能阶段的物理意义可知原因在于：储能时涡簧个数越多，储能次数越多，每次储能时涡簧初始转矩越大。在储能阶段末速度为零不变的情况下，则需要的储能阶段初始速度越大，又由于储能阶段初始速度即为自由下落阶段的末速度，故而自由下落阶段的位移随着涡簧个数的增大而增大，随着储能次数的增多而增大。

图9 储能阶段涡簧总形变量Fig.9 The change of total deformation in the stage of energy storage

图10 储能阶段涡簧相对形变量Fig.10 The change of relative deformation in the stage of energy storage

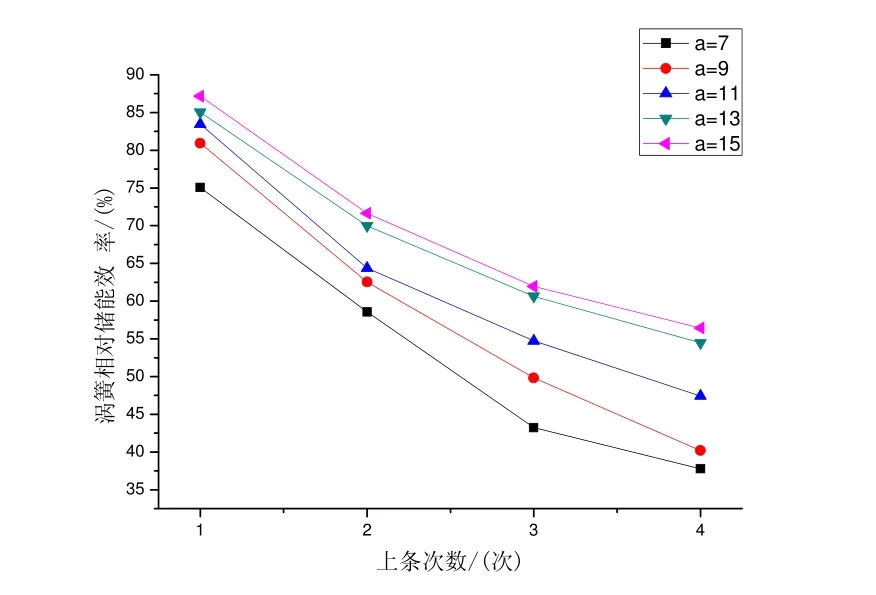
图11 储能阶段涡簧相对储能效率Fig.11 The change of relative deformation in the stage of energy storage

由图8、图9可知，涡簧的相对压缩圈数随着涡簧个数的增加而减小，随着储能次数的增加而减小，此外每次储能过程的总压缩圈数随着随着涡簧个数的增加而减小。通过定性分析涡簧特性曲线可知可：其原因在于随着储能次数的增加，或者涡簧个数的增加，每次储能时涡簧的初始转矩逐渐增加，由于总储能量基本不变，故涡簧相对储能圈数逐渐减小。

由图11可知，涡簧相对储能效率随着储能次数的增加而减小，随着涡簧个数的增加而增大，分析原因在涡簧个数越大，涡簧总刚度越大，储能过程速度变化越快，则阻力因素对系统的影响越小，储能效率越高。而在涡簧个数不变的情况下，每次储能时涡簧的初始转矩随着储能次数的增加而增大，从而导致在储能过程中涡簧产生的阻力越大，故相对储能效率越低。

3.2 用于通风的机械能输出

图12 涡簧组输出功率变化Fig.12 The change of output power about the flat scroll spring group

由输出系统结构可知，在摆轮游丝擒纵调速机构参数不变、涡簧无能量输入且由芯轴驱动输出能量的情况下，n释放由ia决定，现令涡簧个数a=2且涡簧处于充满状态，故可通过改变ia实现输出功率变化，现令ia=0.0025、0.5、0.95、1.9，则n释放分别为 1.47r/min、6r/min、11.45r/min、22.91r/min，释放时间分别为12min、2.94min、1.54min、0.77min。以式（7）编写程序计算涡簧输出的瞬时功率随释放位移的变化情况，如图12所示。由该图可知涡簧组输出的瞬时功率随着涡簧组释放位移的增大而减小，由于涡簧最小输出转矩不为零，故涡簧组输出的瞬时功率在末时刻也不为零。此外对于同一时刻而言涡簧组输出的瞬时功率以及瞬时功率变化率随涡簧组释放速度的增大而增大，在图中表现为P4>P3>P2>P1，k4>k3>k2>k1，在不考虑由加速轮系b产生的能量损耗的情况下，涡簧组释放的瞬时功率即为风机获得的功率。由于ib不变，故风机转速不变，由于风机风量Q1:Q2=n1:n2，故在涡簧释能过程中，风机风量保持恒定。

3.4 输入、输出同时进行

由2.2可知本文中所设计的储能装置中输出系统驱动部件为涡簧轴，且涡簧盒固定，故决定了能量输入与输出不能同步进行，此处若将输出系统驱动部件为涡簧盒，则可实现能量输入输出的同步进行。

自由下落阶段运动方程同2.2.1，储能阶段运动方程为：

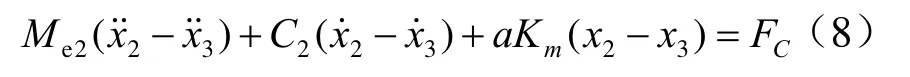
x3为涡簧外端释放能量过程中，角位移θ折算为x方向的直线位移，考虑到任一时刻涡簧储能量大于零，故x3表达式应满足以下约束条件：

现令n释放为 1.47r/min、6r/min、11.45r/min、22.91r/min，将其等效到x方向，其中x3的计算公式为x3=2π×(n释放i)×R/60（R=0.0998m，转盘半径），分别带入以上释放转速可得其x方向的等效速度为 0.0154m/s、0.0629m/s、0.12m/s、0.24m/s，编写程序，可得涡簧组动态储能量、输入涡簧组的能量、涡簧组输出功率随重物下降高度的变化，分别如图13、图14、图15所示。

图13 涡簧组动态储能量变化Fig.13 The dynamic energy storage variation of the flat scroll spring group

图14 输入涡簧组的能量变化Fig.14 The input energy storage variation of the flat scroll spring group

根据涡簧动态等效位移结合式（6）计算涡簧输出转矩，再根据式（7）计算涡簧组输出功率，以上过程通过Matlab编程实现，得出图15所示结果。

图15 涡簧组输出功率变化Fig.15 The change of output power about the flat scroll spring group

由图13可知在当x=0～2.1m期间，对于同一时刻而言，涡簧组储能量随涡簧组释放速度的增加而增加，当x=2.1～5.6m期间，对于同一时刻而言，涡簧组储能量随涡簧组释放速度的增加而减小。由图14可知在储能阶段的任意时刻，输入涡簧组的能量随涡簧组释放速度的增加而增加，原因在于涡簧组存储的重力势能相同，故输入涡簧的能量随着涡簧组释放能量的增大而增大。由图15可知，在涡簧输入与输出能量同步进行的过程中，涡簧组输出功率与重物下降高度不再是线性关系。且在储能阶段的任意时刻，涡簧组输出功率随涡簧组释放速度呈现先增大而增加，在图中表示为P1>P2>P3>P4。此外当涡簧释放速度较低时，涡簧输出瞬时功率基本不变，随着涡簧释放速度的增加，涡簧输出瞬时功率随着重物下降高度的递增而有所增加，且增加幅度依次增大，在不考虑由加速轮系b产生的能量损耗的情况下，涡簧组释放的瞬时功率即为风机获得的功率，此外在此过程中风机风量始终保持不变。

4 结论

本文以平面涡卷弹簧为核心储能原件，设计储能装置并用于车库升降机械重力势能二次回收，将回收能量用于车库通风排烟，分析结果总结如下：

（1）以涡簧为核心储能部件的储能装置能实现对能量的可控收集与释放，对大型能量采集存储装置的实际具有参考价值。

（2）以重力势能为存储对象，分析能量输入与输出方式，得出储能量以及储能效率随涡簧个数的增加而增大，就本文所选参数分析结果而言储能效率由于涡簧组个数及储能次数不等，在35%～87%间变化。

（3）就能量输出方面，当涡簧仅仅输出能量过程中，涡簧释放功率随着释放速度的增加而增大，随着已释放能量的增加而减小，就本文所选参数分析结果而言输出功率在0.05W～0.67W范围内变化；而当能量输入与输出同时进行时，涡簧释放功率随着释放速度以及重物下降高度的增加而增大，就本文所选参数分析结果而言输出功率在0.05W～1.3W范围内变化。