卧式换热器壳体计算方法的研究

赵金凤

摘要： 本文首先建立了符合卧式换热器受力特点的力学模型，并对模型进行力学分析。再从JB/T4731计算各个应力的基本原理出发，通过对比分析卧式换热器自身的特点讨论适合的计算方法，最终形成一套计算校核卧式换热器壳体应力的方法。

Abstract： This paper firstly establishes a mechanical model that meets the force characteristics of a horizontal heat exchanger and performs mechanical analysis of the model. Based on the basic principle of calculating each stress in JB/T4731， the appropriate calculation method is discussed by comparing the characteristics of the horizontal heat exchanger itself， and finally a method for calculating and checking the stress of the shell of the horizontal heat exchanger is formed.

关键词： 卧式换热器； Zick法；轴向应力；切向剪应力；周向应力

Key words： horizontal heat exchanger；Zick method；axial stress；tangential shear stress；circumferential stress

中图分类号：TK172 文献标识码：A 文章编号：1006-4311（2018）16-0209-04

0 引言

卧式容器的标准JB/T4731所采用的计算方法是经典的Zick法。该法的力学模型是将容器简化为外伸的简支梁，其承受的载荷是对称的，而且除考虑封头及其液柱静压影响外，大部分载荷基本是均布的。卧式换热器由于其结构特殊性，载荷并不能保证是对称的，而且两端或一端管板处往往承受着较大的集中载荷，大部分载荷并非是均布的。

根据实际情况，计算长度L选取为：

①固定管板式，取两管板密封面之间的距离，对于焊接式以管板与管箱焊缝为基准；

②U型管板式，取管板管程侧密封面到壳程封头切线的距离；

③浮头式换热器，取壳程两法兰密封面之间的距离，外头盖作为一侧的管箱处理。

而卧式换热器的各个重量分解如下：

①壳程壳体（包括其附件）及其物料的重量均布在计算长度L上，作为均布载荷考虑；

②管束（含管板及换热管，浮头式换热器还包括浮头部件）及其物料的重量按计算模型两端或一端承受的集中载荷考虑；

③管箱（或外头盖）及其物料重量按集中载荷考虑，作用点在管箱重心处，并将力平移至计算模型的端部，相应附加一个弯矩。

1 力学模型的建立与分析

前面已经对卧式换热器的受力情况作了初步分析，所承受的载荷也作了分解，外伸简支梁的力学模型如图1。

1.1 各个载荷的计算

首先定义各个分解载荷的质量：m1—壳程壳体（包括附件）及其物料的质量，kg；m2—管束（含管板及换热管，浮头式换热器还包括浮头部件）及其物料的质量，kg；m3—管箱1及其物料的质量，kg；m4—管箱2及其物料的质量，对于U型管板式取0，浮头式取外头盖质量，kg；其它参数：L1—管箱1整体长度，mm；L2—管箱2整体长度，mm；q—均布载荷，N/mm；G1—管箱1一侧集中载荷，N；G2—管箱2一侧集中载荷，N。则各个载荷的计算如表1所示。

1.2 支反力及内力的计算

基于图1外伸简支梁的力学模型进行分析，可得到各处的弯矩，鞍座处的剪力及支座反力等需要的力。定义参数：A1——管箱1一側鞍座到基准的距离；A2——管箱2一侧鞍座到基准的距离。

1.2.1 支座反力

首先来考虑两个鞍座的支反力，其中F1表示管箱1一侧鞍座处支反力，F2表示管箱2一侧鞍座处支反力。

1.2.2 两鞍座之间的弯矩

这里，两鞍座之间的弯矩我们只需要计算极值：

1.2.3 支座处弯矩

支座处弯矩两个鞍座分别计算：

1.2.4 支座处剪力

由于两处鞍座各有两个值（鞍座两侧），因此需计算四个剪力：

至此各个所需要外力和内力均已经得到表达式，其关键是各个重量的分解。

2 轴向应力的计算

考虑到实际情况，一般换热器鞍座的位置由于有壳程出口接管的缘故，很难满足封头起加强作用的假设条件。加强圈也基本不会用在卧式换热器上。因此，本文轴向应力的计算只考虑鞍座平面上无加强圈且封头不起加强作用的情况。

筒体的轴向应力主要由两部分组成，分别由设计压力和弯曲内力产生。对于弯矩的符号，依据一般规定，使梁变形呈上凹状的为正，上凸为负，前者使得筒体截面的高点受压缩应力，后者受拉伸应力。

2.1 两鞍座之间轴向应力的计算

计算用弯矩取极值，则弯矩M1按式（3）计算。该处的轴向应力计算可按式（11）和式（12）。

其中：Pc——壳程筒体设计压力，MPa；δe——壳程筒体有效厚度，mm；Ra——壳程圆筒的平均半径，mm。

两鞍座之间的弯矩由于两端集中载荷的缘故，M1可能会是负值，而不像均布对称载荷那样永远为正。但由于该处筒体圆环截面为完整的，负值只是使得式（11）和（12）的结果互为颠倒，不影响最后的校核。

2.2 鞍座处轴向应力的计算

鞍座处的弯矩考虑到载荷的非对称性，需分别计算两个支座处的值，按式（5）和（6）。这里两处的弯矩一定仍然是负值，与标准中的情况一致，计算用弯矩M2取式（5）和（6）计算结果绝对值较大值。轴向应力计算可以按式（13）和（14）。

2.3 系数K1和K2

注意到式（13）和式（14）分别有系数K1和K2。Zick法中假设鞍座平面无加强圈且封头不起加强作用的圆环截面是不完整的，认为承载轴向应力的截面范围是2（θ/2+β/6），其中θ为鞍座包角，β=π-θ/2。基于这样的假设，不完整圆环截面对应σ3和σ4的抗弯模量可以积分求得，将完整圆环截面抗弯模量πRe之外的多项式整合提取出来，便分别是K1和K2，它们最终只和包角θ相关。

这两个系数值的表达式较为繁琐，其常用值可按表2选取，与标准中的值一致。

值得注意的是，因为不考虑加强，鞍座包角的增大可以改善鞍座处轴向应力的应力水平。

3 切向剪应力的计算

卧式容器所计算的切向剪应力，在材料力学中的概念是弯曲剪应力，它与弯曲内力息息相关。一般梁跨度远大于横截面的尺寸，弯曲剪应力不是主要因素，不会考虑去计算校核。但如果梁跨度较短而截面较高时，就需要考虑弯曲剪应力对强度的影响了。卧式容器我们知道属于后者，一般筒体的长度相对直径不是很长，这时候就需要考虑校核该应力了。

考虑到弯曲内力在微段左右两侧横截面上存在差异，维持微段力的平衡只能由纵截面上剪力来平衡，根据剪力互等原理，便得到了横截面上的弯曲剪应力。因为是与纵截面上的剪力互等的，对于圆环截面弯曲剪应力只能是切向的，所以称为切向剪应力。与弯曲内力类似，在横截面上是呈一定规律分布的，完整圆环截面的最大值在水平两点。其最大值的计算公式借用矩形截面的公式，近似表示为式（15）：

3.1 最大切向剪应力的计算

式（18）是完整圆环截面切向剪应力的计算公式。与前面计算轴向力时一样，本文切向剪应力的计算也只考虑鞍座平面上无加强圈且封头不起加强作用的情况。对此，Zick法有两点假设：①此时切向剪应力与完整截面的值关系如式（19）；②其承载截面包角为2（θ/2+β/20），最大值在该截面的最高点。

3.2 系数K3

系数K3仍然是和鞍座包角有关的，是取切向剪应力最大值时对应的角度得到的值，这里取值和标准一致，按表3。

4 鞍座处周向应力的计算

由于本文不考虑带加强圈的情况，所以鞍座处周向应力需计算两个位置的应力值，分别是最低点处和鞍座边角处（垫板起加强作用时还考虑垫板边角处）。其计算过程颇为复杂，详见文献[1]和[4]。

这里首先给出结论：这两点的应力计算公式可以完全采用原标准中的公式计算，只是其中的支反力F要按本文中的式（1）和式（2）取值。

先来分析一下最低点的周向应力。其计算过程先是根据不完整截面上切向力竖直分量的和等于支反力，而得到该切向力。则不完整截面上该切向力总和就是周向压缩力，这个周向压缩力再除以承载面积即得到周向应力。过程中巧妙的借助了弯曲剪应力分布规律，即式（18）乘以δe（线力），但其中剪力V并不是之前式（21）计算的值，完全两个概念，只是一个纯粹为了使得它所产生的按既定规律分布在不完整截面上的切向剪力竖直分量可以平衡支反力而已。

边角处的周向应力也是如此，该处的应力值不但有最低点同理产生的应力值（但计算方法不同，Zick法在这里假设是支反力的1/4），还考虑曲梁效应产生的弯曲内力。其中曲梁上分布的切向剪力是一样的道理，只是该切向剪力是从完整截面出发计算的，即整个截面上剪力就是支反力，再按既定规律分布线力。最终未被加强截面再通过修正其系数得到。

通过以上分析我们知道，周向应力抛开截面尺寸和包角大小的因素，就取决于支反力的大小了，而与外载荷分布形式等无关。也就证明了本节开头的结论。

但需要注意的是，由于系数的选取和鞍座到离基准的距离A有关，单单将支反力F取F1和F2的最大值计算还存在不确定性，因此本文认为应分别用式（1）和（2）的结果各自计算，最终取应力值的最大值。

4.1 两个关键的假设

4.1.1 垫板起加强作用的条件

三个条件已经众所周知：①垫板厚度不小于筒体厚度0.6倍；②垫板宽度不小于有效宽度b2，b2按式（22）计算；③垫板包角不小于鞍座包角加12°。

4.1.2 承载周向弯矩有效截面的長度

承载周向弯矩有效截面的长度取值如下：①当L/Ra≥8时，为圆筒中径的4倍；②当L/Ra<8时，为筒体长度一半。

4.2 最低点的周向应力计算

4.2.1 垫板不起加强作用

4.2.2 垫板起加强作用

注意式（23）和（24）仅适用于筒体焊接在鞍座上的情况。

4.3 鞍座边角处的周向应力计算

4.3.1 垫板不起加强作用

4.3.2 垫板起加强作用

4.4 垫板边角处的周向应力计算

该处应力只在垫板起加强作用时计算。

当L/Ra≥8时：

当L/Ra<8 时：

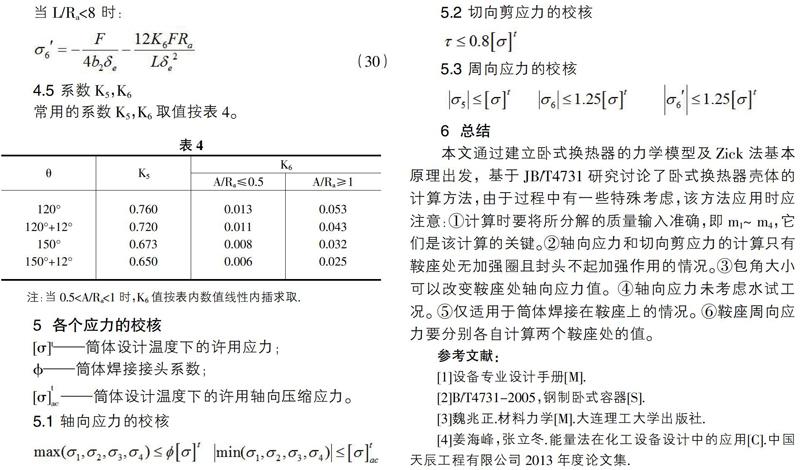
4.5 系数K5，K6

常用的系数K5，K6取值按表4。

5 各个应力的校核

5.1 轴向应力的校核

5.2 切向剪应力的校核

5.3 周向应力的校核

6 总结

本文通过建立卧式换热器的力学模型及Zick法基本原理出发，基于JB/T4731研究讨论了卧式换热器壳体的计算方法，由于过程中有一些特殊考虑，该方法应用时应注意：①计算时要将所分解的质量输入准确，即m1～ m4，它们是该计算的关键。②轴向应力和切向剪应力的计算只有鞍座处无加强圈且封头不起加强作用的情况。③包角大小可以改变鞍座处轴向应力值。④轴向应力未考虑水试工况。⑤仅适用于筒体焊接在鞍座上的情况。⑥鞍座周向应力要分别各自计算两个鞍座处的值。

参考文献：

[1]设备专业设计手册[M].

[2]B/T4731-2005，钢制卧式容器[S].

[3]魏兆正.材料力学[M].大连理工大学出版社.

[4]姜海峰，张立冬.能量法在化工设备设计中的应用[C].中国天辰工程有限公司2013年度论文集.